基于偏最小二乘线性判别分析的遗传算法在代谢组学特征筛选中的应用*

武海滨 张 涛 赵发林 李 康

基于偏最小二乘线性判别分析的遗传算法在代谢组学特征筛选中的应用*

武海滨1张 涛2赵发林3李 康4△

目的 探讨基于偏最小二乘线性判别分析的遗传算法特征筛选性能，并将其应用于高维代谢组学数据。方法 通过模拟试验验证基于偏最小二乘线性判别分析的遗传算法特征筛选能力，同时应用于卵巢良恶性肿瘤鉴别的代谢组学数据特征筛选分析。结果 模拟实验显示，基于偏最小二乘线性判别分析的遗传算法对信息变量的筛选能力明显优于偏最小二乘变量投影重要性指标;代谢组学数据分析显示，使用遗传算法筛选出的变量能够获得更低的误差率，该方法筛得的变量具有更大的概率包含了与某种生物学结果相关的代谢物。结论 基于偏最小二乘线性判别分析的遗传算法作为一种优化技术，在小样本条件下对高维数据的特征筛选具有较好的效果。

偏最小二乘 判别分析 遗传算法 代谢组学

*:国家自然科学基金资助(81172767)

1.浙江省疾病预防控制中心(310051)

2．山东大学公共卫生学院流行病与卫生统计学系

3.杭州师范大学医药卫生管理学院

4.哈尔滨医科大学卫生统计学教研室

△通讯作者:李康，E－mail:likang@ems.hrbmu.edu.cn

代谢组学通常使用理化分析技术对生物体体液或组织的小分子代谢物进行定量的动态测量，继而利用统计学方法识别与病理生理刺激或基因改变相关的代谢物，探索可能的代谢途径。基于分析技术的进步，如LC-MS，GC-MS和NMR，近年来代谢组学迅速发展，并成功地应用于医学、毒理学和营养学等领域〔1－4〕。当前的分析技术能够产生高通量的代谢指纹图谱数据，包含丰富的信息，但也对数据的分析提出了挑战。首先，代谢物的数量远大于观测例数，很容易导致模型过拟合的发生;其次，很难确定哪些代谢物与某种生物学结果密切相关。

偏最小二乘(partial least squares，PLS)能够较好地处理多重共线性和小样本数据，已经成为光谱学和化学计量学领域的一种基本方法，在代谢组学中也具有广泛应用〔5－6〕。但是，有研究指出当存在大量噪声变量时，PLS仍易过度拟合数据，产生过于“理想”的结果〔7〕。代谢指纹图谱数据中代谢物的数目远大于观测数目，并且包含大量无关的代谢物，很容易导致机会性分类，因此在模型建立之前有必要先进行特征筛选。PLS模型中的变量投影重要性(variable importance in the projection，VIP)指标能够直观地显示每个变量的重要程度，已被广泛应用于代谢组学研究中的特征筛选〔8－9〕。然而，数据中大量的噪声变量可能对VIP产生影响，而且生物标记物之间复杂的相互作用可能比独立的基本效应更加重要〔10〕。为处理上述问题，本研究提出了基于偏最小二乘线性判别分析(partial least squares linear discriminant analysis，PLSLDA)的遗传算法(genetic algorithm，GA)用于特征筛选。

原理与方法

1.偏最小二乘线性判别分析

PLS最初为一种回归方法，它通过建立正交得分向量(或称潜变量、成分、因子等)间接拟合解释变量集和反应变量集之间的线性关系。由于PLS简单、灵活，能够提取相关的信息，最近被广泛应用于降维、分类、可视化、特征筛选等问题〔11－12〕。PLSLDA 是 PLS用于分类问题的一种方法，已被用于基因组和代谢组的研究〔13－14〕，该方法的第一步是通过特征提取获得k个得分向量t1，…，tk。假定数据集包含n个观测、m个解释变量和反应变量Y，对于分类问题Y可以使用不同的整数表示(Y=1，…，q)，若q=2，Y可以按照连续型变量直接处理，若q＞2，Y则需转换成q个哑变量后进行处理:

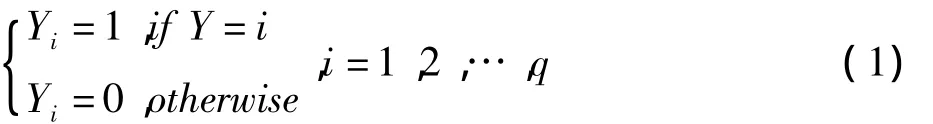
因此，解释变量和反应变量矩阵可以分别表示为Xn×m和Yn×q。假定数据已经标准化，PLS 按照如下方式将两个矩阵分解成得分和载荷的乘积形式:

(2)式中Tn×k和Un×k是提取出的k个得分向量，Pm×k和Qq×k是相应的载荷矩阵，En×m和Fn×q表示残差矩阵。正交得分向量通过最大化解释变量和反应变量之间的协方差获得，即在约束条件wTw=1，cTc=1，和tTu最大的条件下计算向量t和u。向量t和u分别表示矩阵T和U的某一列，w和c是相应的权重向量，权重向量计算的不同定义了不同的PLS算法，经典的非线性迭代偏最小二乘算法(nonlinear iterative partial least squares，NIPALS)中权重向量w和c可以通过下面的特征值问题来解决〔15〕:

在获得了w和c后，可以计算出t=Xw和u=Yc的值。进而，矩阵X和Y减去t和u所包含的信息，再进行第二轮得分向量的提取。上述过程不断重复进行直到达到指定的收敛标准。

第二步即使用得分向量t1，…，tk作为预测变量进行线性判别分析。由于选择的PLS得分向量个数k远小于变量个数m，使用近似正态分布的得分向量进行线性判别分析时能够获得较为理想的结果。得分向量个数k是PLSLDA中唯一需要优化的参数，通常使用交叉验证来选择。

在得分向量提取的过程中，每个自变量权重的绝对值表示它们在相应得分向量中影响的大小，而得分向量具有进行分类的能力，因此自变量的权重可以表示它们在相应得分向量中的重要性。第j个自变量在第r个得分向量中变量影响的平方()为其相应权重的平方()乘以第r个得分向量所解释总变异的百分比，VIP是对自变量在提取的k个得分向量中VIN的综合:

2.遗传算法

遗传算法(GA)的基本原理类似于自然界的进化和自然选择过程。首先，GA使用简单的编码技术将搜索空间映射到基因空间，接着通过适者生存的机制从初始种群中进化问题的解。在进化过程中，GA通过染色体的复制(replication)、交叉(crossover)和变异(mutation)等遗传过程不断进化出新的子代，那些具有较高适应性的染色体具有更高的概率将它们的信息传递给下一代，保证了GA的搜索方向逐渐向最优解靠近，同时防止出现局部最优。由于GA能够在复杂或高维空间中搜索最优或近似最优的解，该方法被广泛应用于优化问题，这里将GA作为一种特征筛选策略使用。

本研究中，每一个变量被定义为遗传算法中的一个基因，从所有m个基因中随机选取g个基因构成一个染色体，每个染色体表示问题的一个可能的解，c个染色体构成了一个小生境(niche)，w个小生境构成了初始种群。小生境各自独立进化，它们之间可以按照一定的概率间或交换染色体，这一过程称为迁移(migration)。适应函数(fitness function)用于评估进化过程中每个染色体的适应性，常用的如准确率、误差率或AUC等，本方法对种群内每一代的每个染色体建立PLSLDA模型，并使用交叉验证的判别准确率来评价染色体的适应性。适应性较高的染色体具有更高的概率将它们的信息传递给下一代。整个GA过程在适应函数的约束下，通过一系列不断重复的复制、交叉、变异和迁移等操作逐渐提高染色体的适应性。为避免子代的最大适应性出现较大波动，可以按一定概率保留适应性最高的染色体进入子代且不进行交叉和变异，这一过程即精英主义(elitism)。进化很多代以后，若某个染色体的适应性大于等于设定的目标值，将该染色体作为最优染色体选择出来，流程见图1。当获得了足够数量的最优染色体后，那些在最优染色体中多次出现的基因表明在多变量背景下对于分类具有重要作用〔16〕，因此可以根据变量在最优染色体中出现的频率来判断其重要性。该算法与其他基于PLS的遗传算法存在着差异，如Ramadan的研究结果〔6〕。首先，我们将该方法用于超高效液相色谱与质谱联用仪(UPLC-QTOF/MS)的代谢指纹图谱数据，该方法获得的代谢物个数远大于NRM;其次，在算法中变量采用整数编码，以便控制染色体长度;最后，使用多种群的方法进化出上千个染色体能够获得较稳健的结果。本研究使用R软件包galgo〔17〕来完成遗传算法的进化过程，使用plsgenomics软件包实现PLSLDA。

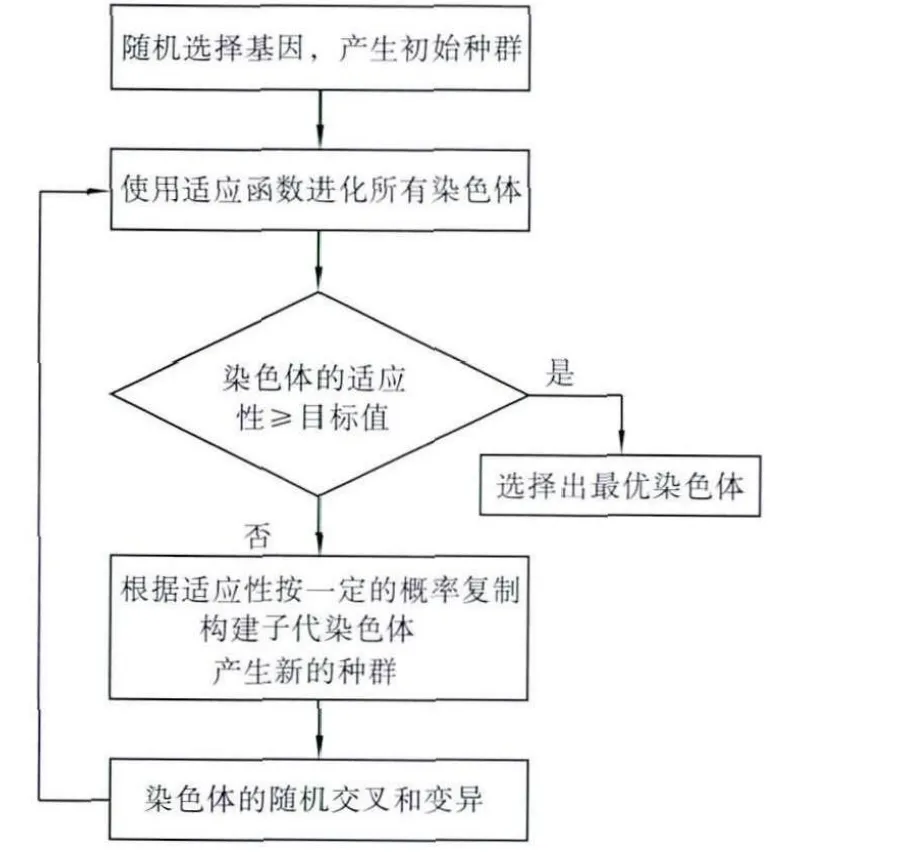
图1 遗传算法的基本流程

模拟实验

代谢指纹图谱数据通常具有数以万计的代谢物，多变量的模式使上述问题更为复杂，为对比 GAPLSLDA和VIP的特征筛选性能，我们设计了多变量模式的模拟数据，并模拟实际工作中的小样本情况。首先，独立产生1000个服从N(0，1)的噪声变量，然后产生两组差异变量，每组包含3个差异变量，最后将这6个变量放在模拟数据集中指定的位置。为简单起见，本模拟试验中的差异变量均设为二分类变量，信息变量的产生原理见图2。设有3个信息变量X1，X2，X3和1个反应变量Y，信息变量被设定同时作用于反应变量，且假定3个信息变量同等重要，信息变量值为1时表示“高表达”，0表示“低表达”，3个信息变量共有8种不同的组合方式，假定只有1个“高表达”的情况为“正常状态”，出现2个或3个“高表达”时为“癌症状态”。为了减少每个变量的主效应，我们设定了这种组合的构成比例:出现三个“低表达”和三个“高表达”的概率均为0.1。根据预先指定的概率，进行重复抽样，产生30个“正常观测”和30个“癌症观测”，最后重复上述过程100次。

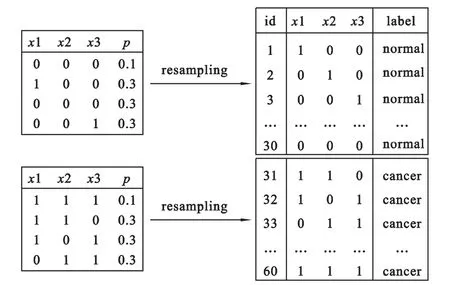
图2 差异变量的产生原理

由于两种特征筛选方法均能够对所有变量进行排序，我们使用6个差异变量排序的频率分布来演示结果(100次重复，600个排序)。图3是两种方法对差异变量排序的频率分布图(排序前100位)，可以看出两个分布均为正偏态，但GA-PLSLDA筛选出的差异变量排序更为向前集中，VIP筛选出的差异变量排序具有较多的右拖尾。GA-PLSLDA能够将90.0%的信息变量排在前6位，99.5%的差异变量排在前100位中，而 VIP仅将 56.3%的差异变量排在前 6位，91.7%的差异变量排在前100位中，显示GA-PLSLDA比VIP具有更优的特征筛选能力，该方法受噪声影响较小，能够较好地处理多变量模式。其他的模拟实验证实，在变量数目一定，如果增加样本量(如n1=n2=100)，这种差别会逐渐减小，但GA-PLSLDA方法筛选的结果仍然明显优于VIP的方法。

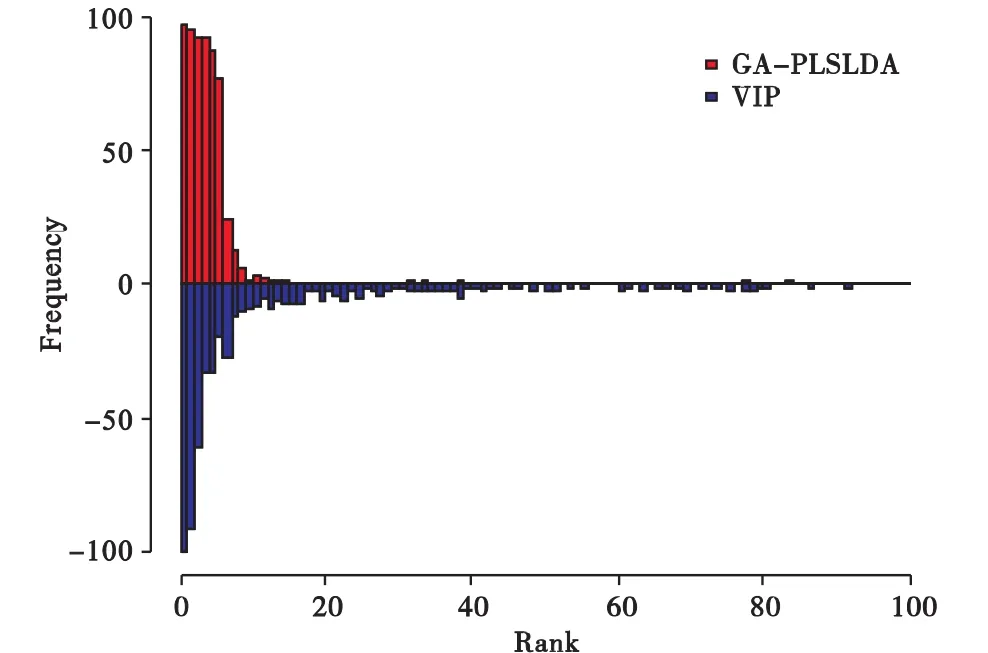
图3 GA-PLSLDA和VIP对差异变量排序的频率分布图(排序前100位)

实例分析

收集37例首次发现的原发性卵巢癌患者和54例卵巢囊肿患者尿样，采用超高效液相色谱与质谱联用仪(UPLC-QTOF)检测，分别分析正离子(ESI+)和负离子(ESI－)模式，数据集的说明见表1。

表1 卵巢癌患者血浆代谢指纹图谱数据集概况

由于代谢指纹图谱数据变量个数太多，如直接使用遗传算法进行变量筛选，运算负荷过大，因此，首先使用单变量的过滤法删除最不相关的一些变量。本研究使用基于两独立样本t检验的置换检验(permutation test)，进行10000次置换，双侧P＜0.1的变量构成候选数据集，使用R软件包multtest完成该过程。最后，分别使用GA-PLSLDA和VIP从候选数据集中选择简单有效的变量子集。

在遗传算法中设定交叉概率为0.5，交叉点可以是染色体的任何位置，每个染色体均发生变异，适应函数为PLSLDA 5折交叉验证的预测准确率。小生境个数、小生境规模、染色体长度和最大进化代数见表2，其他参数使用默认设定，对每个数据集分别进化1000个最优染色体以增强结果的稳定性。

表2 遗传算法参数设置

分别选择这两种算法变量筛选排序前50位的变量，并逐个比较它们预测的误差率，如PLSLDA具有较低的分类误差率，模型可能包含对分类具有重要作用的变量。由于数据集样本量较小，此处采用e.632+误差率，选择100个Bootstrap样本进行计算。图4为两种特征筛选方法排序前50的变量判别误差率的逐个比较，表3为排序前50的变量获得的最小判别误差率。由此可见，进行特征筛选后PLSLDA的判别误差率明显小于未进行特征筛选，特征筛选能够有效地减少无关代谢物的影响，提高分类的准确性。在变量个数相同时GA-PLSLDA筛选出的变量一般比VIP能够获得更低的误差率，这表明GA-PLSLDA更能够排除无关代谢物的影响，有效地降低分类误差率，该方法筛得的变量具有更大的概率包含了与某种生物学结果密切相关的代谢物。

图4 卵巢癌代谢指纹图谱数据判别误差率的比较

表3 排序前50的变量PLSLDA最小判别误差率

小 结

代谢指纹图谱数据中样本例数较小，代谢物的数量巨大，很容易对PLS产生影响，导致机会性分类。因此，特征筛选具有重要的意义，该过程能够有效地降低模型的复杂性，提高分类器的预测性能，并可以发现可能的生物标记物。本研究提出了一种基于PLSLDA和GA的特征筛选方法，该方法通过限制染色体的长度控制进化过程中模型的复杂性，噪声变量在每个染色体中的影响可以变得较小，从而降低了过拟合的风险。另外，在GA-PLSLDA的进化过程中会建立成千上万的PLSLDA模型，考虑了变量之间复杂的相互作用，能够发现多变量的模式。最后，通过进化出相当数目的最优染色体可以使结果更加稳健。

本研究通过模拟试验和实例分析证明了GAPLSLDA在特征筛选上优于代谢组学中经常使用的VIP指标，能够处理复杂的多变量模式。虽然该方法具有较好的特征筛选性能，但是它需要设定较多的参数，运算负荷相对较大;此外，一些无关变量偶尔能够伴随生物标记物出现在染色体上，增加了特征筛选的假发现率，需要进一步探索;最后，由于运算负荷较大，本研究实例分析中未使用双重交叉验证，计算出的误差率可能会比实际偏低，而样本量对结果的具体影响，仍需进一步研究。

1．Greef J，Smilde AK．Symbiosis of chemometrics and metabolomics:Past，present，and future．Journal of Chemometrics，2005，19(5 － 7):376-386．

2．Clayton TA，Lindon JC，Cloarec O，et al．Pharmaco-metabonomic phenotyping and personalized drug treatment．Nature，2006，440(7087):1073-1077．

3．Robertson DG．Metabonomics in toxicology:a review．Toxicological Sciences，2005，85(2):809-822．

4．Van Dorsten FA，Daykin CA，Mulder TP，et al．Metabonomics approach to determine metabolic differences between green tea and black tea consumption．Journal of Agricultural and Food Chemistry，2006，54(18):6929-6938．

5．Brindle JT，Antti H，Holmes E，et al．Rapid and noninvasive diagnosis of the presence and severity of coronary heart disease using 1H-NMR-based metabonomics．Nature medicine，2002，8(12):1439-1444．

6．Ramadan Z，Jacobs D，Grigorov M，et al．Metabolic profiling using principal component analysis，discriminant partial least squares，and genetic algorithms．Talanta，2006，68(5):1683-1691．

7．Westerhuis JA，Hoefsloot HCJ，Smit S，et al．Assessment of PLSDA cross validation．Metabolomics，2008，4(1):81-89．

8．Qiu Y，Cai G，Su M，et al．Serum metabolite profiling of human colorectal cancer using GC-TOFMS and UPLC-QTOFMS．Journal of Proteome Research，2009，8(10):4844-4850．

9．Martin JC，Canlet C，Delplanque B，et al．1H NMR metabonomics can differentiate the early atherogenic effect of dairy products in hyperlipidemic hamsters．Atherosclerosis，2009，206(1):127-133．

10．Moore JH．The ubiquitous nature of epistasis in determining susceptibility to common human diseases．Human Heredity，2003，56(1-3):73-82．

11．Boulesteix AL，Strimmer K．Partial least squares:a versatile tool for the analysis of high-dimensional genomic data．Briefings in Bioinformatics，2007，8(1):32-44．

12．荀鹏程，钱国华，赵杨，等．高维生物学数据两阶段组合降维策略研究．中国卫生统计，2012，29(5):626-629．

13．Boulesteix AL．PLS dimension reduction for classification with microarray data．Statistical Applications in Genetics and Molecular Biology，2004，3(1):1544-1561．

14．Taylor SL，Ganti S，Bukanov NO，et al．A metabolomics approach using juvenile cystic mice to identify urinary biomarker and altered pathways in polycystic kidney disease．American Journal of Physiology Renal Physiology，2010，298(4):909-922．

15．钱国华，荀鹏程，陈峰，等．偏最小二乘法降维在微阵列数据判别分析中的应用．中国卫生统计，2007，24(2):120-123．

16．Li L，Weinberg C，Darden T，et al．Gene selection for sample classification based on gene expression data:study of sensitivity to choice of parameters of the GA/KNN method．Bioinformatics，2001，17(12):1131-1142．

17．Trevino V，Falciani F．GALGO:an R package for multivariate variable selection using genetic algorithms．Bioinformatics，2006，22(9):1154-1156．

Genetic Algorithm Based on Partial Least Squares Linear Discriminant Analysis and its Application on Feature Selection of Metabonomics

Wu Haibin，Zhang Tao，Zhao Falin，et al．Department of NCDs Control and Prevention，Zhejiang Center for Disease Control and Prevention(310051)，Hangzhou

ObjectiveEvaluating the feature selection property of the genetic algorithm based on partial least squares linear discriminant analysis，and its application on high dimensional metabolomic data.MethodsValidating the ability of genetic algorithm based on partial least squares linear discriminant analysis with simulated data and applying it on discriminating metabolomic data between benign and malignant ovarian cancer.ResultsSimulations showed that the genetic algorithm based on partial least squares linear discriminant analysis was superior to the index of variable importance in the projection．The analysis on real metabolomics data indicated that using variables selected by genetic algorithm we were able to obtain smaller error rate than the index of variable importance in the projection．The variables selected by genetic algorithm had higher probability involving the metabolites that were related with certain biological results.ConclusionAs an optimization technique，genetic algorithm based on partial least squares linear discriminant analysis could effectively analyze the high dimensional data with small sample size．

Partial least squares;Discriminant analysis;Genetic algorithm;Metabonomics

(责任编辑:刘壮)