40Cr冷滚打成形中位错密度变化研究

王晓强 崔凤奎 燕根鹏 李玉玺

1.河南科技大学，洛阳，471003 2.西安理工大学，西安，710048

0 引言

高速冷滚打成形是金属局部不均匀冷塑性成形，塑性成形过程复杂，成形过程中金属塑性成形问题实质上是金属在多场耦合强作用下的微观组织变化和金属流动问题。影响高速大变形条件下成形过程的外在因素有：变形温度、高变形速度、大变形程度，而影响高速大变形的自身因素是材料在变形过程中微观组织的演变情况。金属的变形和塑性变化的最直接原因是位错运动，金属的宏观变形取决于金属微观组织位错运动受到金属内部能量阻力的状况。金属的塑性成形是加工硬化和回复交织的过程，加工硬化是位错产生以及位错间相互作用的过程，回复是位错在变形过程中抵御外力重新排列、生成、抵消的过程，这两个过程中位错密度变化贯穿其中。因此，研究40Cr在高速冷滚打成形过程中的位错密度变化规律具有重要的意义。

Krapfenbauer［1］首先提出了冷滚打加工工艺，并应用到冷滚打花键和齿轮加工中。Kurz［2］对冷滚打成形过程进行了仿真建模分析，并通过仿真与实验中的击打力、工件坯料的应力值和应变值相对比，验证了仿真模拟的可靠性。Zella等［3］利用有限元方法对渐开线花键在轴对称加载和非轴对称加载情况下的接触情况进行了分析，形象描述了在扭矩不断增大时应力、应变的变化情况和应力集中分布情况，为花键冷滚打过程中应力、应变的求解提供了一种新的方法。徐永福［4］对冷滚打花键金属组织变形、残余应力分布和齿面质量等进行了深入研究，并得出冷滚打加工能够改善花键表层金属组织及残余应力分布状况，使花键强度、齿面质量和完整性得到显著提高的结论。全建辉［5］根据数值模拟的结果，并结合最小阻力定律和体积不可压缩原理对高速冷滚打成形的变形规律和流动特性进行了讨论分析。文献［6－8］建立了丝杠冷滚打机构动力学模型，并对成形原理和模型进行了仿真和实验，验证了丝杠冷滚打成形的可行性；分析了高速冷滚打成形过程中的变形力，并对高速冷滚打进行仿真分析，结合理论分析和实验结果对变形力进行了修正和测量，验证了所建立的解析方程的正确性。崔凤奎等［9］利用分离式 Hopkinson压杆实验装置对40Cr钢进行了压缩试验，获得40Cr钢在不同变形条件下的应力－应变曲线。综上所述，国内外进行冷滚打技术的研究主要集中在冷滚打加工方法和设计理论、冷滚打运动分析、应力与应变的关系及其分布特征和金属流动规律等方面，而在微观组织方面的研究鲜见报道。因此研究冷滚打制件的微观组织变化和流动规律，对提高冷滚打成形质量及其制件的使用性能具有重要的理论价值和工程应用意义。

1 高速大应变率条件下40Cr位错密度变化曲线

通过位错理论总结可知，材料在加工之前，材料内部处于稳定状态，位错密度相对比较低；随着变形的增大，位错密度不断增大，此时材料内的异号位错相互交织进行增减排列，导致材料内部加工硬化大于温度软化效应，引起应力增大。在高速大应变率条件下，由于材料自身加工硬化与动态软化特性的共同作用，应力呈现波浪变化，其微观原因是位错增加和位错减少的作用。为了更好地描述40Cr材料塑性变形的组织结构变化，把位错密度作为中间变量引入到传统的应力应变关系中。

流变应力σ与位错密度ρ的关系为［10］

式中，M为泰勒因子常数，本文取M＝2；u为剪切模量，u＝800GPa；b为柏氏矢量，b＝3.3×10－8cm；α为材料常数，α＝0.3。

将式（1）与文献［9］中40Cr应力应变曲线结合，得到40Cr在不同应变率ε·下位错密度变化曲线，如图1所示。

由图1可知，在同一应变率下，位错密度随温度变化明显，呈现出位错密度随温度降低而增大的趋势。出现该现象的主要原因是：温度的升高使得热激活过程增强，进而使金属内部位错出现攀移运动；温度升高使材料的临界剪应力、滑移系增加，进而使位错的滑动阻力减小，变形抗力减小；温度越高，原子的热振动越剧烈，晶格中的原子平衡被打破。原子在高速击打力的作用下沿着应力场梯度方向不断运动，使金属在瞬间产生塑性变形；位错的连续运动和自身平衡状态的激变使应力－应变曲线呈现出起伏变化。

2 基于位错密度变化的微观组织演变模型建立及分析

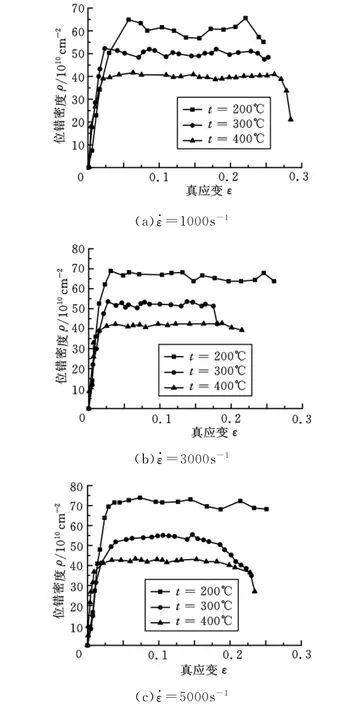
图1 不同应变速率下位错密度曲线

40Cr在高速、大变形击打过程中应力－应变曲线呈波浪状起伏变化，本质上是由材料在变形速度、变形程度、变形温度的影响下位错密度的增减所引起的。整个变形过程中位错密度变化与宏观因素之间的关系［11］如下：

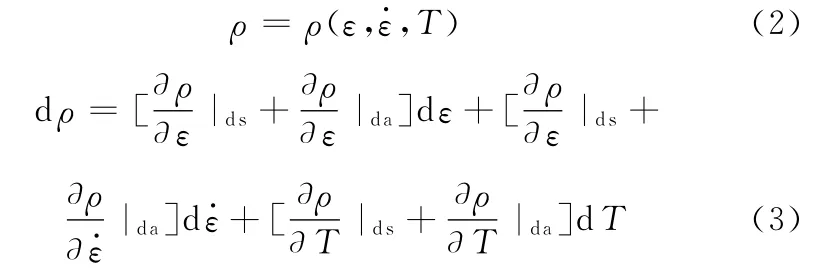
式中，ε为应变为应变率，s－1；T为变形温度；da表示位错增加；ds表示位错减少。

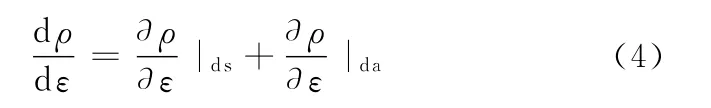
研究表明，材料位错密度的平方根与位错密度增加和减少相关［12-13］，由此可得

式中，k2、k3分别为材料在变形过程中的硬化系数和软化系数。

由式（4）～式（6）得到材料位错密度变化表达式为

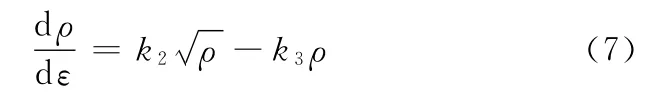
当变形过程达到峰值应力时，位错密度变化处在平衡状态，位错密度增加和减少相平衡，即可得

式中，ρs为峰值应力时的位错密度。

由式（7）积分可得

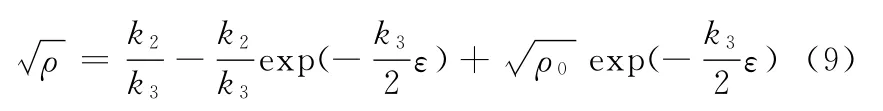
式中，ρ0为初始应力时的位错密度。

根据应力应变曲线和Zener－Hollomon方程，求得

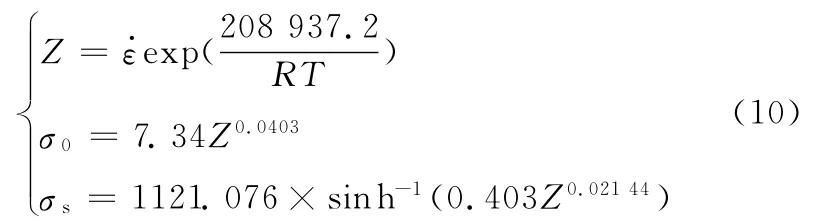
式中，Z为Zener－Hollomon参数，为依赖于流变应力的温度补偿因子；R为摩尔气体常数，取值为8.314J／（mol·K）；σ0为初始应力；σs为峰值应力。

根据宏观应力流动模型，得到微观位错密度变化模型：

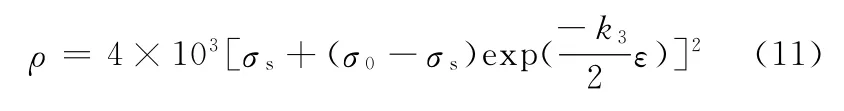
利用式（11）得到不同应变率下位错密度实验值和计算值随应变变化曲线，如图2所示。由图2可知：位错密度实验值和计算值均随应变率的增大而增加，呈现应变率敏感性；在同一应变率不同温度下，位错密度实验值和计算值随温度的升高而减小，呈现温度负敏感性；位错密度实验值和计算值存在一定偏差，其原因在于微观位错变化模型的参数选取与宏观实验数据密切相关，且宏观实验条件设定、实验数据记录、峰值应力选取、材料参数均存在不可避免的误差。位错密度实验值和计算值整体上基本吻合，从微观层面为宏观变化提供了有力支持，使宏观变化和微观变化相结合。

3 高速冷滚打条件下40Cr材料XRD实验研究

3.1 实验方案

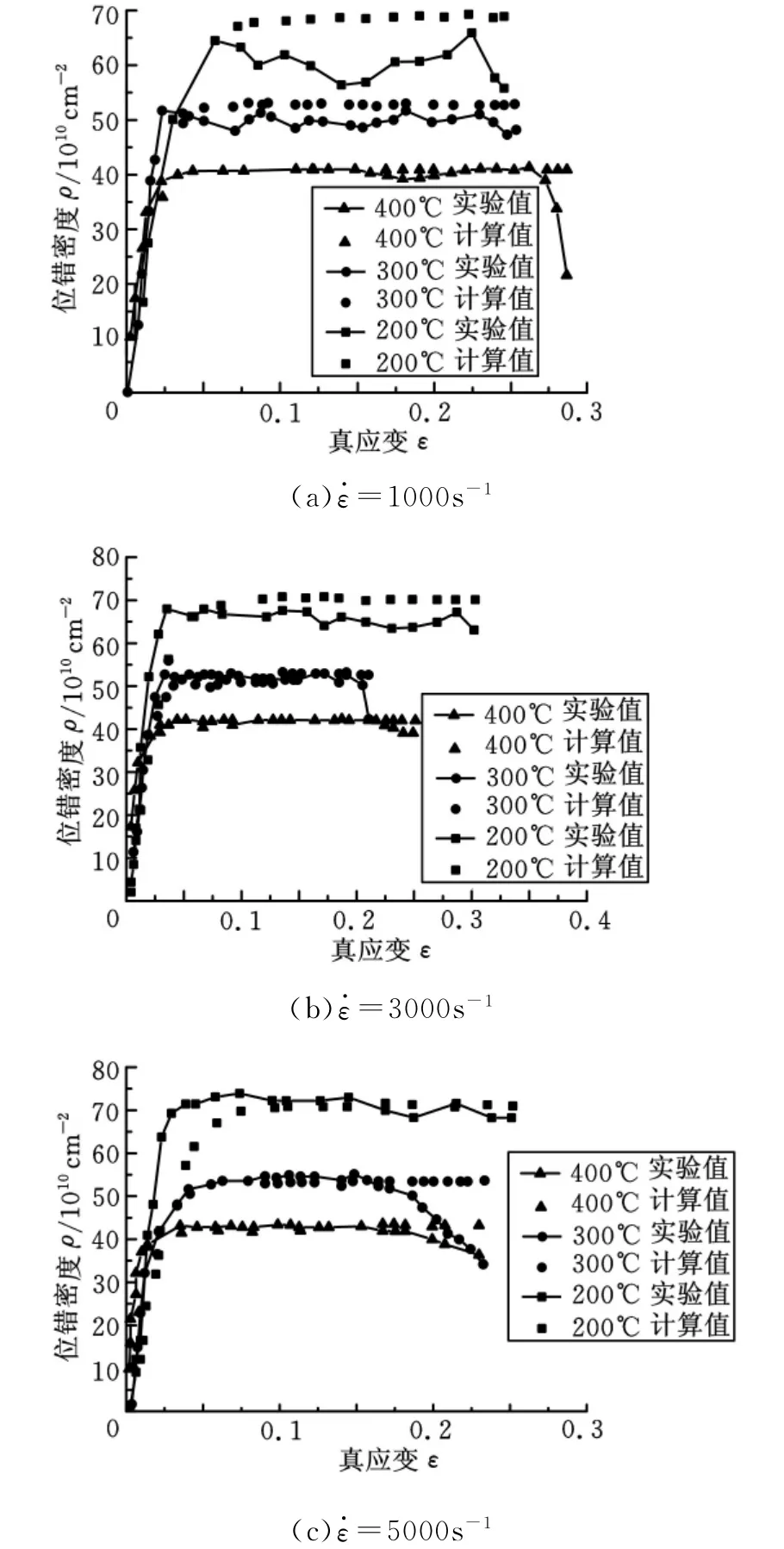
图2 不同应变率下位错密度计算值和实验值曲线

本实验采用德国布鲁克D8AX射线衍射仪，在该实验系统上对高速冷滚打过程中不同变形条件下40Cr材料进行XRD实验，实验条件如下：12个试样分4组，每组3个；实验温度分别是100℃、200℃、300℃、400℃，应变率分别为1000s－1、3000s－1、5000s－1。

3.2 实验结果及分析

利用XRD对不同变形条件的试样分晶面进行分析，提取40Cr材料衍射比较明显的（110）晶面、（200）晶面、（211）晶面三个晶面的图谱，如图3所示。

采用积分法求解峰半高宽，作峰底的切线，测量峰面积和峰高度，用面积除以高度得到峰宽。利用MDI Jade 5.0软件提取不同变形条件下的峰半高宽β，如表1所示。根据Dunn等的研究可知，位错密度和峰半高宽之间的关系式［14－15］为

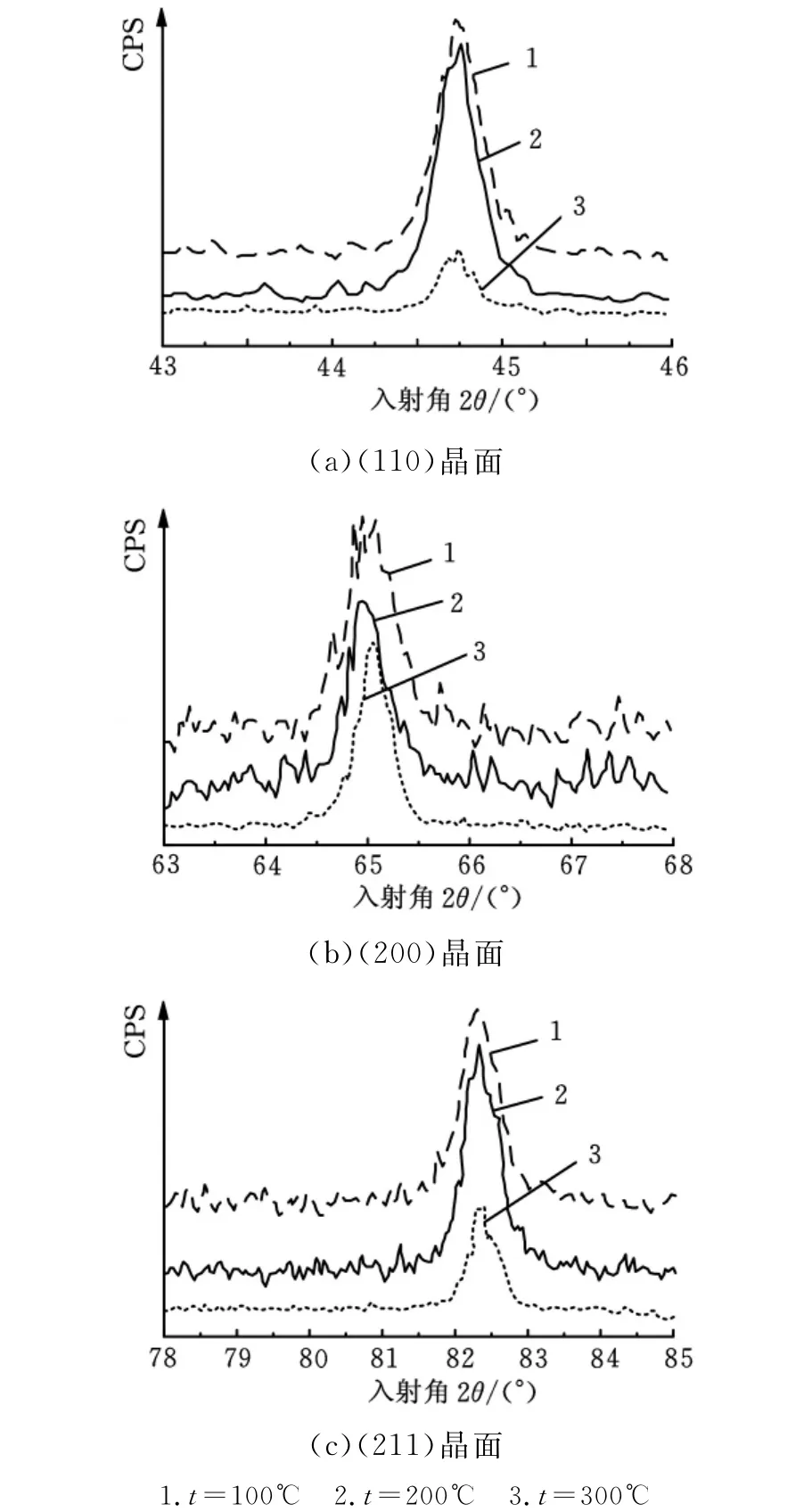
图3 应变率为3000／s时不同温度条件下的晶面图谱

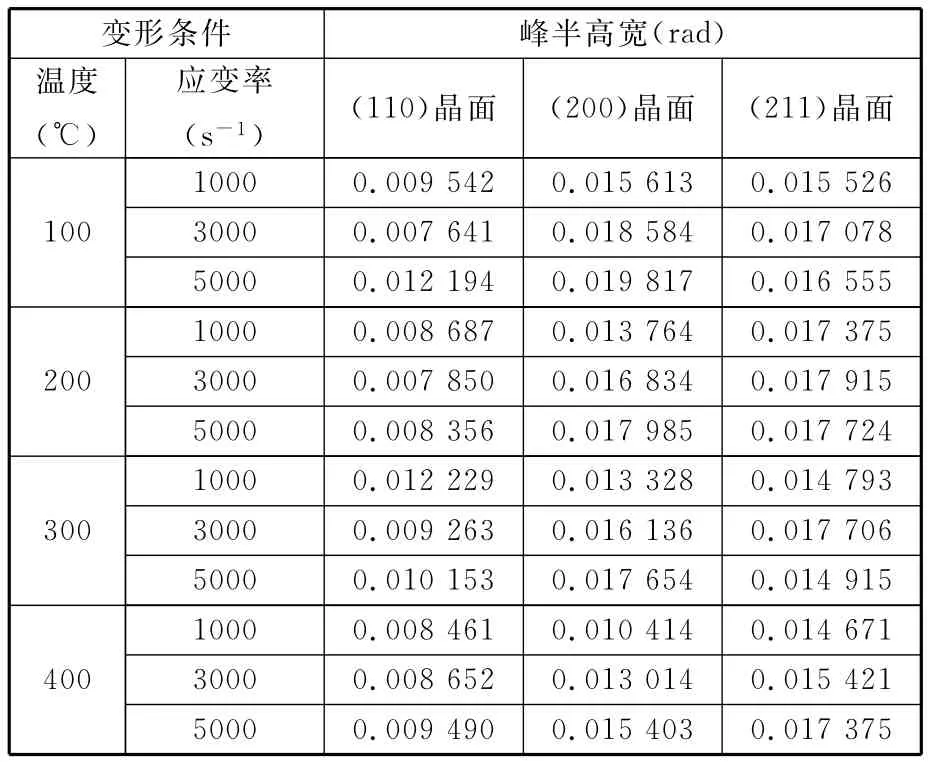
表1 不同变形条件的峰半高宽

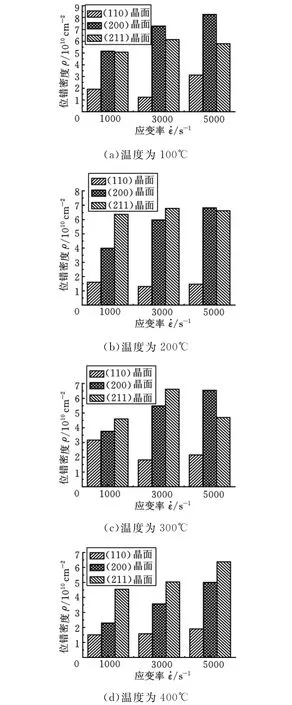
图4 不同应变率下各个晶面位错密度

根据式（12）与表1数据求得各个晶面的位错密度，并进行对比分析，如图4所示。由图4可知，温度为100℃时，（200）晶面的位错密度最大，（110）晶面的位错密度最小；同一变形条件下（200）晶面所受应变力最大，大量位错被启动，位错密度快速增加，晶面变形最大，金属流动最快。温度为200℃时，（211）晶面位错密度最大且波动不大，（110）晶面位错密度最小；随着温度的升高，（211）晶面内部微观组织滑移开动呈现加快趋势，导致（211）晶面位错密度增长很快，说明此变形条件下（211）晶面更易发生滑移，宏观表现为（211）晶面金属变形快速增加，金属向（211）晶面区域流动。温度为300℃时，1000s－1、3000s－1应变率下（110）晶面、（200）晶面、（211）晶面的位错密度随应变率增大而增加，5000s－1应变率下（200）晶面位错密度高于（211）晶面位错密度；由于在5000s－1应变率下（200）晶面发生晶格畸变和滑移，造成（200）晶面的位错密度快速增加，改变之前的位错密度变化趋势，宏观上变现为应力集中发生在（200）晶面区域。温度为400℃时，3个晶面的位错密度随应变率的增大呈现出不断增大趋势，（211）晶面位错密度最大且增加很迅速；由于工件内部微观组织受到外界击打力影响内部变化呈趋势性变化，工件内部变化稳定，未发生晶格畸变，位错在内部变化平稳，金属流动比较稳定。综上可知：不同的变形条件下各个晶面位错密度变化不同，位错密度受变形条件的影响较大且不同晶面的位错密度变化不同。

在不同变形条件下对3个晶面的位错密度之和进行整体对比，如图5所示。由图5a可知：3个晶面的位错密度之和随温度升高而减小；同一温度下随应变率增大而增大。由于随着温度升高，金属内部的活动逐渐剧烈，易于发生温度软化效应，位错密度不断被抵消减少，故呈现出随温度升高而减小现象。由图5b可知：3个晶面的位错密度之和随应变率增大而增加，在同一应变率下随着温度升高而减小。位错密度随应变率的增大而增加，主要由于大变形量促使晶格畸变和快速滑移，促使位错密度在短时间内迅速增加。整体的变化趋势和微观模型位错密度变化的趋势相一致，这主要是由于XRD测定仅是选取比较明显的典型性晶面峰值，在局部范围对微观位错密度变化进行定量分析。

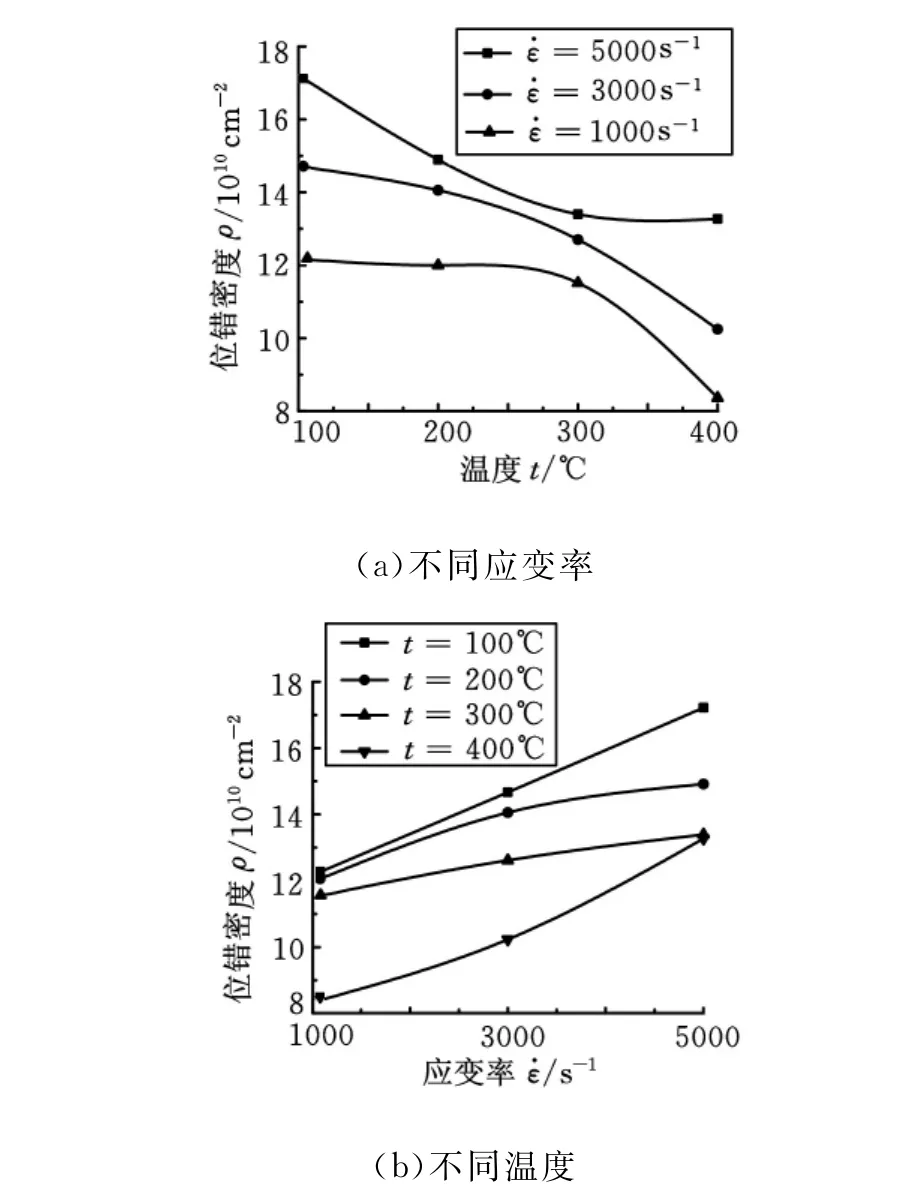
图5 不同变形条件下晶面整体位错密度

4 结论

①将40Cr冷滚打宏观应力变化和位错密度变化机理相结合，得到40Cr在不同应变率下位错密度变化曲线；随温度降低而依次增加，呈现出位错密度随温度降低而增加的趋势；同一应变率不同温度条件下，位错密度随温度变化明显；在不同应变率下，位错密度随温度降低而增加的趋势贯穿整个过程。②基于位错密度变化的微观组织演变模型建立了40Cr位错密度变化模型；通过模型验证和分析，位错密度实验值和计算值整体上基本吻合，从微观层面为宏观变化提供了有力支持。③通过XRD实验得到40Cr在不同变形条件的XRD图谱，利用Dunn公式求得40Cr在不同变形条件下各个晶面及晶面整体位错密度；位错密度变化受变形条件的影响较大且不同晶面的位错密度变化不同，3个晶面位错密度整体上的变化趋势和微观模型位错密度变化的趋势相一致，进一步从微观角度解释了40Cr在冷滚打成形过程中的变化规律。

［1］Krapfenbauer H.New Aspects for the Mass Production of Spur Gears by Cold Rolling［J］.IPE International Industrial ＆Production Engineering，1984，89（3）：39－41.

［2］Kurz N.Theoretical and Experimental Investigations of the“Grob”Cold Shape－Rolling Process［C］／／Twenty－fifth International Machine Tool Design and Research Conference.Birmingham，1985：551－559.

［3］Zella L，Kahn J，Suzanne W.Finite Element Analysis of an Involute Spline［J］.Journal of Mechanical Design，2000，122（2）：239－244.

［4］徐永福.冷滚打花键动力学分析与仿真［D］.洛阳：河南科技大学，2008.

［5］全建辉.基于ANSYS／LS－DYNA的花键冷滚轧成形机理研究［D］.洛阳：河南科技大学，2007.

［6］李言，杨明顺，李玢，等.丝杠冷滚打成形动力学仿真及分析［J］.西安理工大学学报，2009，25（4）：383－387.Li Yan，Yang Mingshun，Li Bin，et al.Dynamics Simulation and Analysis of Lead Screw Cold Roll Beating［J］.Journal of Xi’an University of Technology，2009，25（4）：383－387.

［7］张璐，杨明顺，李言，等.高速冷滚打过程变形力解析方 法 及 其 修 正 ［J］.塑 性 工 程 学 报，2011，18（5）：1－7.

［8］张璐，李言，杨明顺，等.丝杠冷滚打成形过程金属流动规律研究［J］.中国机械工程，2012，23（13）：1623－1628.Zhang Lu，Li Yan，Yang Mingshun，et al.Study on Metal Flowing of Lead Screw Cold Roll－beating Forming［J］.China Mechanical Engineering，2012，23（13）：1623－1628.

［9］崔凤奎，郭超，李玉玺.40Cr钢的塑性流动应力特征及本构关系［J］.河南科技大学学报，2012，33（6）：1－5.Cui Fengkui，Guo Chao，Li Yuxi.Flow Stress Characteristics and Dynamic Constitutive Model for 40Cr Steel［J］.Journal of Henan University of Science ＆Technology，2012，33（6）：1－5.

［10］Merking H，Kocks U F.Kinetics of Flow and Strain－Hardening［J］.Acta Metallurgic，1981，29（11）：1865－1875.

［11］El－Danaf E A，Soliman M S，Almajid A A.Effect of Solution Heat Treatment on the Hot Workability of Al－Mg－Si Alloy［J］.Materials and Manufacturing Processes，2009，6（24）：637－643.

［12］Mecking H，Kocks U F.Kinetics of Flow and Strain－hardening［J］.Acta Meta，1981，29（11）：1865－1875.

［13］Estrin Y.Unified Constitutive Laws of Plastic Deformation［M］.New York：Academic Press，1996.

［14］贾仁需，张玉明，张义门，等.XRD法计算4H－SiC外延单晶中的位错密度［J］.光谱学与光谱分析，2010，30（7）：1995－1997.Jia Renxu，Zhang Yuming，Zhang Yimen，et al.Calculation of Dislocation Destiny Using X－Ray Diffraction for 4H－SiC Homoepitaxial Layers［J］.Spectroscopy and Spectral Analysis，2010，30（7）：1995－1997.

［15］张纪才，王建峰，王玉田，等.In源流量与Ⅲ族流量之比对InGaN／GaN多量子阱性质的影响［J］.物理学报，2004，53（8）：2467－2471.Zhang Jicai，Wang Jianfeng，Wang Yutian，et al.Effect of the Ratio of TMIn Flow to GroupⅢFlow on the Properties of InGaN／GaN Multiple Quantum Wells［J］.Acta Physica Sinica，2004，53（8）：2467－2471.