双前桥转向系与悬架运动协调性分析及优化

刘振声 赵 亮，2

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082 2.柳州孔辉汽车科技有限公司，柳州，545007

0 引言

重型汽车的行驶工况一般比较恶劣，且双前桥转向系统相对复杂，容易造成严重的轮胎磨损和跑偏。国内对双轴转向优化方法的研究较多［1－2］，如文献［1］对双前桥转向杆系进行了空间优化分析，文献［2］对非独立悬架与转向传动机构运动干涉分析方法进行了研究。目前全面考虑悬架运动不协调对转向的影响以及双前桥转向系运动特性的研究还不完善。

本文结合板簧变形运动学分析方法来计算非独立悬架和转向传动机构的空间运动干涉量，并对双前桥转向的空间四连杆传动机构的运动特性进行分析，进而结合以上两方面因素对轮胎磨损的影响进行优化。

1 板簧模型和转向特性分析

1.1 板簧变形运动学

此前，大部分文献在分析悬架运动干涉过程中，对板簧的运动轨迹都采用圆弧近似算法。文献［3］中给出了当板簧弧高y发生变化时，主片安装点P的水平坐标x变化规律的精确表达式，避免了错误的应用。

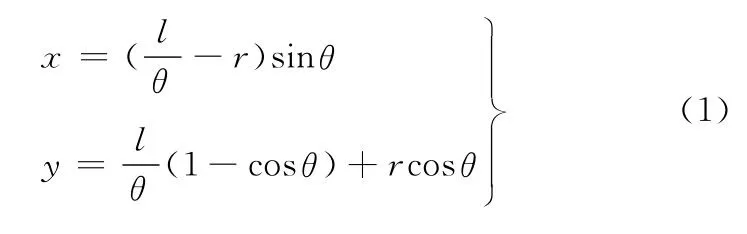
根据图1可得主片安装点坐标随板簧变形的运动关系式如下：式中，r为主片卷耳中心线半径；l为板簧半长；θ为参变量张角。

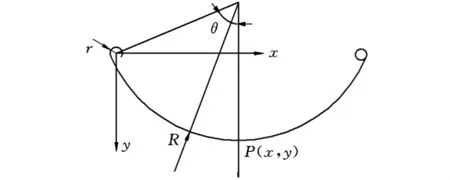
图1 板簧变形示意图

因θ通常是很小的值，为了计算简便，可取3阶以下的泰勒展开式近似表达，1－cosθ＝θ2／2，式（1）可简化为

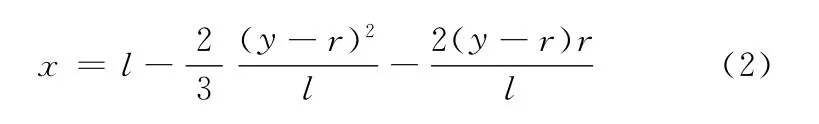
式（2）表明，主片安装点运动轨迹并非单纯的圆弧，而是条抛物线。在给定板簧弧高y时，可得x的数值解。

1.2 转向杆系与悬架干涉空间模型

整车坐标系oxyz中，规定坐标系原点为一桥轴线中间点，车辆前进行驶的反向为x轴正方向，面向汽车前进方向指向右侧为y轴正方向，z轴正方向为垂直向上［4］。

针对此前平面分析法的局限性和分析误差，建立基于整车硬点坐标的空间干涉模型，如图2所示。

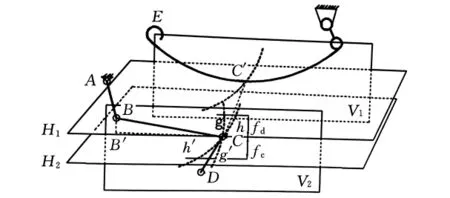
图2 悬架与转向直拉杆干涉示意图

图2 中，H1面为过板簧主片安装点C′的水平面；H2面过转向节臂球销中心点C并与H1面平行；板簧中心面为V1，与H1、H2面垂直；V2面过球销点C且平行于V1面。另外，A点为转向摇臂与转向机的安装位置，B为摇臂与直拉杆安装点，B′为B点在H2面内的投影，D点为C点向主销中心线的投影位置，E点为板簧卷耳中心点。

当完成整车总布置初步方案后，各个设计硬点（A、B、C、C′、D）的坐标即能确定。在车轮上下跳动时，转向节臂球销中心点C一方面绕B点在B、B′、C所确定的平面内摆动，同时受板簧变形的影响，随着主片安装点C′的坐标变化规律在V2面内摆动，运动轨迹由式（2）确定。如图2所示，当在V2面内分别取悬架静挠度fc和动挠度fd时，若只考虑如上单一因素下C点的摆动时，轨迹分别为gg′和hh′，因此，转向直拉杆和悬架运动干涉量为线段gh和g′h′的长度。

为便于分析，建立局部坐标系BXYZ，以B点为原点，坐标轴方向与整车坐标系一致。列出C点分别在转向直拉杆和板簧变形影响下的运动方程式。

在局部坐标系BXYZ中，C点坐标为

B′点坐标为（0，0，ZC）。C点绕局部坐标系原点B（0，0，0）作圆弧摆动的轨迹方程为

此外，C点在B、B′、C所确定的平面内摆动，根据四点共面方程，用行列式表示共面的三个向量混积为0，即

给定任意的悬架挠度f（规定悬架压缩时f为正值），此时Z＝f＋ZC。将Z值代入式（4）、式（5），即可得出在有挠度f的情形下C点位置（X，Y，Z）。

同时，转向节臂球销中心点C和板簧主片安装点C′为平动关系，在有挠度f情形下，C′点在V1面内摆动，此时安装点P的弧高为

将式（6）代入式（2），即可得安装点P的水平坐标x。此时转向节臂球销中心点C在局部坐标系BXYZ下X坐标为

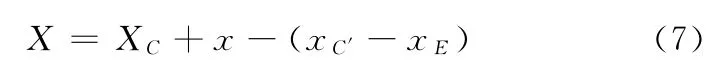
若分别取悬架动挠度fd和静挠度fc，即可得出图2中点g、h和g′、h′的坐标。此时，转向直拉杆与悬架的运动不协调量分别为

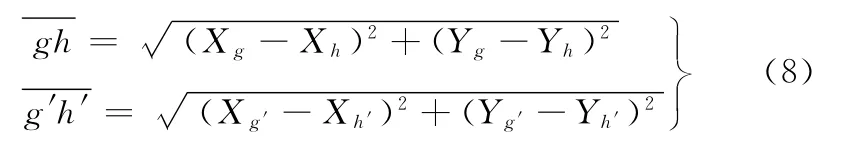
1.3 双前桥转向特性

对于利用双前桥转向的多轴汽车，为保证所有车轮都处于纯滚动状态，则要求所有车轮的轴线都相交于一点，即相交于转动中心［5］。由图3可见，同一车桥的内外轮转角都应满足阿克曼转向原理：

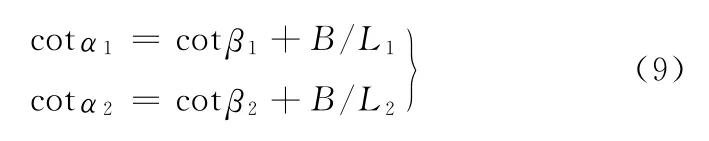
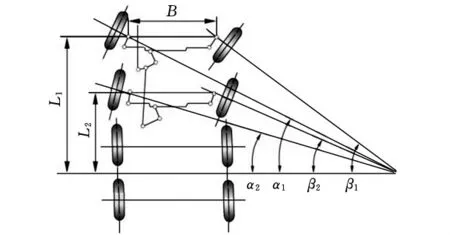
图3 四轴汽车双前桥转向示意图

不同车桥的同侧转向轮转角也应满足如下关系：

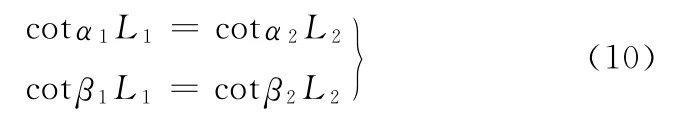
式中，α1、α2为第一、二桥左轮转角；β1、β2为第一、二桥右轮转角；B为两侧主销轴线与地面相交点之间的距离；L1、L2分别为一桥、二桥轴线至假想后桥中心线的距离。

式（9）和式（10）分别由转向梯形机构和双摇臂驱动机构保证。

有关转向梯形机构的研究已经很成熟［6］，故本文主要研究双摇臂连杆结构布置对异轴同侧转向轮转角关系的影响。

各级摇臂的旋转轴线并不一定平行，且摇臂在车架上的安装位置不一定在同一纵面内，两根摇臂和中间拉杆构成了图4所示的空间四连杆机构。

图4中，K1、K2为摇臂与中间拉杆的安装点，A1、A2为摇臂与转向机的安装位置。在整车硬点布置后，K1、K2、A1、A2以及各级摇臂的旋转轴轴向即可确定。因此，摇臂的旋转中心O1（O2）点坐标可通过K1（K2）点作垂直于摇臂旋转轴线的直线所得的垂足得出。摇臂的初始摆角α、β以及摇臂的等效长度m、n可通过各个设计硬点坐标值计算得出。

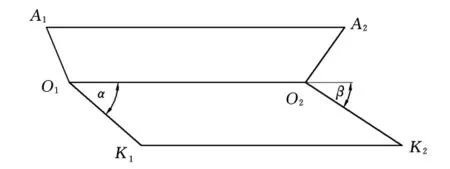
图4 双摇臂空间四连杆机构

设定一组一桥左轮转角α1，求得对应的第一摇臂摆角α，即可确定球销点K1各状态下的坐标，从而确定K2点的坐标以及第二摇臂的摆角β，进而得出二桥左轮的转角α2。

2 双前桥转向优化设计

通过上述分析可以总结出，轮胎在行驶过程中出现异常磨损的主因是车辆在坏路面上转向时转向系与悬架的运动干涉。因此，在转向系优化的同时，还应将路面引起的干涉量作为设计目标［7］。

2.1 设计变量

在各个杆系与车架安装点保持不变的情况下，参考图2取一、二级摇臂与转向直拉杆的安装点B1、B2，转向节臂球销中心点C1、C2，以及图4中两根摇臂和中间拉杆的连接点K1、K2的坐标值作为设计变量。

2.2 约束条件

受布置空间的影响，各个变量的坐标值约束在其设计的最大允许范围内：

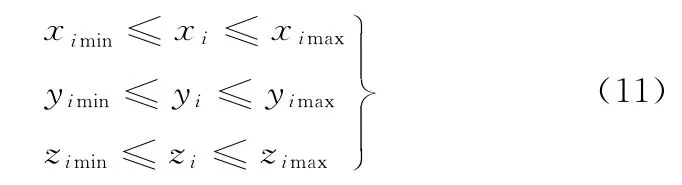
2.3 目标函数

由于一、二桥悬架结构相同，故将前桥干涉量叠加作为优化目标：

式中，fd1、fd2分别为满载状态下，车轮最大上下跳动时悬架的动挠度值分别为一、二桥干涉量。

根据式（10），求出二桥左转向轮的理论转角α′2＝f（α1），取实际转角与理论转角的差值，根据最小二乘法建立目标函数，保证双前桥转向系传动机构的正确布置：

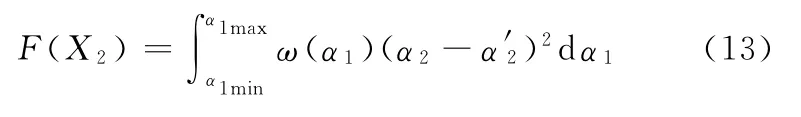
α1的常用转角为［－25°，25°］，因此加权因子一般取：

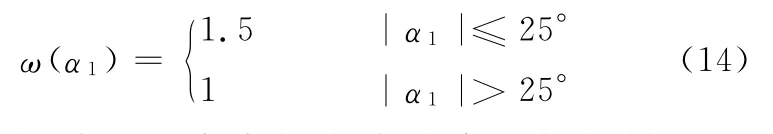
降低轮胎的异常磨损应当结合悬架与转向杆系的干涉量与双前桥的正确转向特性，得出优化函数为

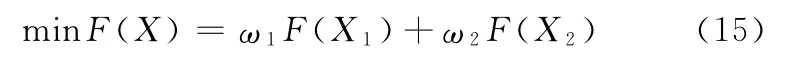
当实车中悬架与转向杆系的干涉量对轮胎跑偏的影响较大时，加权因子的选取应ω1≥ω2；反之，则ω1＜ω2。

3 双前桥转向优化结果

以企业某8×4重型车为例，通过MATLAB编写M优化程序，得到优化前后结果曲线如图5～图7所示。

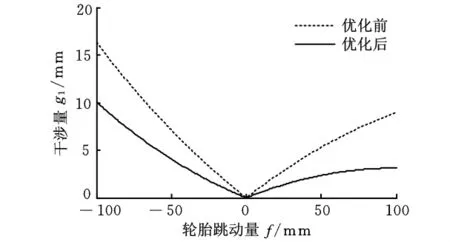
图5 一桥悬架与转向系干涉量

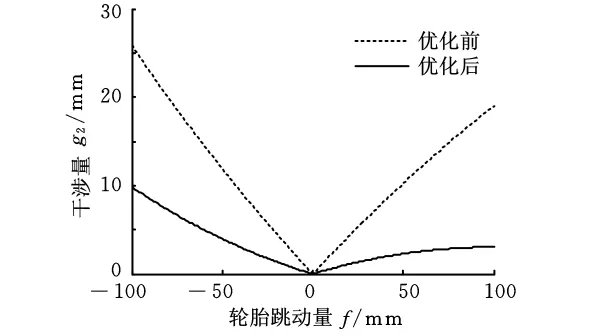
图6 二桥悬架与转向系干涉量

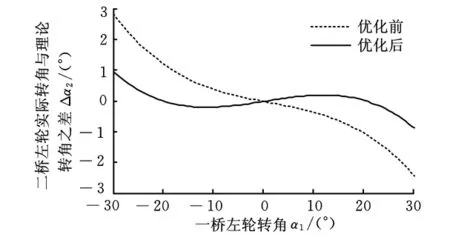
图7 转向特性优化结果

图5 ～图7说明，悬架与转向杆系干涉量在优化后得到了较大的改善，且在常用转角范围内，一、二桥转向轮的实际转角关系明显优于优化之前，减轻了轮胎的磨损和跑偏。

4 结束语

通过结果分析，证明此优化方法有效，且本文对悬架与转向直拉杆运动的干涉量分析与计算方法，以及双前桥转向特性的理论研究是正确的。采用分析的方案，能够较好地减轻实车出现的轮胎磨损和车辆跑偏。

［1］唐应时，李克，黄自强，等.双前桥转向杆系的空间优化分析［J］.汽车技术，2006，22（8）：22－25.Tang Yingshi，Li Ke，Huang Ziqiang，et al.Spacial Optimization Analysis of Dual－front Axle Steering System ［J］.Automobile Technology，2006，22（8）：22－25.

［2］古玉峰，赵稳庄，方宗德.非独立悬架与转向传动机构运动干涉分析方法研究［J］.机械设计，2009，26（12）：52－54.Gu Yufeng，Zhao Wenzhuang，Fang Zongde.Analytical Method Research on the Movement Interference of Non－independent Suspension and Steering Transmission Mechanism［J］.Journal of Machine Design，2009，26（12）：52－54.

［3］郭孔辉.板簧变形运动学分析及其应用［J］.汽车工程，1990（2）：7－15.Guo Konghui.Analysis and Applications of Leaf Spring Kinematics［J］.Automotive Engineering，1990，2：7－15.

［4］张洪欣.汽车设计［M］.2版.北京：机械工业出版社，1996.

［5］陈家瑞.汽车构造［M］.2版.北京：机械工业出版社，2009.

［6］杨新明.多轴转向汽车运动分析与仿真［D］.武汉：武汉理工大学，2003.

［7］陈黎卿，王社会，郑泉，等.基于遗传算法的汽车非独立悬架与转向匹配优化设计［J］.河南科技大学学报，2008，29（3）：27－30.Chen Liqing，Wang Shehui，Zheng Quan，et al.Optimal Design of Dependent Suspension and Steering Match Based on Genetic Algorithm［J］.Journal of Henan University of Science ＆ Technology（Natural Science），2008，29（3）：27－30.