基于响应面法的液压平板车车架结构优化

王新彦 戈余丽 桂 天 张胜文 王 琪

1.江苏科技大学，镇江，212013 2.密西西比大学，牛津，38655

0 引言

平板车是对货物水平运输的理想高效运输设备，在船厂、码头、火车站、机场、大型工厂、仓库等物料搬运场所被广泛使用。我国对此类重型车车架设计及强度校核多依靠经典的材料力学、弹性力学等传统的经验和方法，其缺点是会造成应力分布不均，强度分配不合理，而且设计周期长，设计成本高。可靠性设计考虑了随机因素对安全性的影响，更能揭示事物的本来面貌，提供全面的信息，避免了传统方法追求保险导致过分保守的设计，从而能够节约原材料、降低成本并带来较大的经济效益。为了更好地研究车架应力与结构之间的关系，常需要构造其显式表达，多项式响应面法是解决此类问题应用较为广泛的方法，Kaymaz等［1］通过加权响应面法进行结构的可靠性分析，Wong等［2］将载荷步法运用到响应面法中进行了可靠性分析，Knill等［3］利用缩减项的响应面模型来预测高速民用运输机（HSCT）超音速阻力的欧拉解。但是在进行基于响应面法的可靠性分析时容易出现回归矩阵奇异的现象［4］。本文在使用上述方法进行常规编程求解时，在迭代计算至第二步时便程序报错，发生矩阵奇异情况，导致计算无法进行。

针对上述问题，本文以320t液压平板车车架为例进行了如下的探索：①首先进行了静应力试验及有限元分析，确定了危险部位，并以危险部位车架腹板孔口处圆角半径、薄板厚度和长度为设计变量，运用回归设计方法获得了响应面函数，确保响应面函数为最优回归；②利用响应面函数构建显式约束条件，进行车架的轻量化设计；③在响应面函数已知的情况下，结合可靠性理论，对车架结构进行可靠性分析。

1 车架有限元分析及应力试验

根据车架结构及载荷的对称性，利用ANSYS软件的参数化设计语言建立1／4液压平板车车架参数化有限元模型。车架材料为Q345，弹性模量为206GPa，泊松比为0.3，密度为7850kg／m3。采用shell63单元，参考单元边长为20mm。

车辆静止时，车架承受的静载荷由车身和车架的自身质量、车架上各总成与附属件质量及有效载荷组成。本文主要考虑车架自重、置物架质量10t以及满载质量320t，忽略附件影响。车辆行驶时车架受到的动载荷作用可用动载荷系数来衡量。平板车有6组轴线，采用液压悬挂，具有良好的减振性能，由文献［5］，可取动载荷系数为1.26。加载时，将静载荷乘以动载系数所得的动载荷施加在相应的作用节点上。对平板车车架而言，最常见及影响较大的工况为满载弯曲。平板车车架通过回旋支撑与悬架相连，将悬架与车架接触部分的中间4个环形区域节点进行全约束，其余部分约束Z方向位移。对于本文1／4车架模型，只需在左边的环形接触区域进行全约束，其余两处约束Z方向位移，另外在对称中心面上施加对称约束，如图1所示。

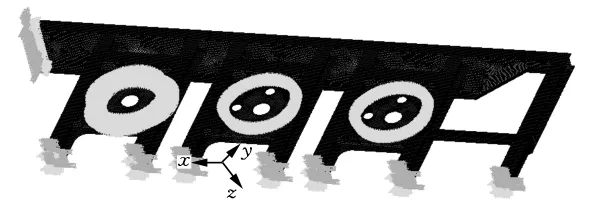
图1 1／4车架边界约束

由有限元分析结果可知，车架最大von Miss等效应力为159.829MPa（图2），发生在车架横梁上翼板焊接处，与焊接质量有关。次大值发生在横梁之间的腹板圆角处，为143.799MPa（图2圆圈处），说明此位置存在应力集中现象。

图2 车架有限元应力分析结果

对某平板车进行应力试验（图3），选取车辆满载静止和车辆满载并以1km／h匀速行驶两种工况。取车架板件连接部位及圆角等截面突变位置作为试验点进行应力试验，具体位置如图4所示，箭头所指即是腹板处试验点位置。

图3 应力现场试验

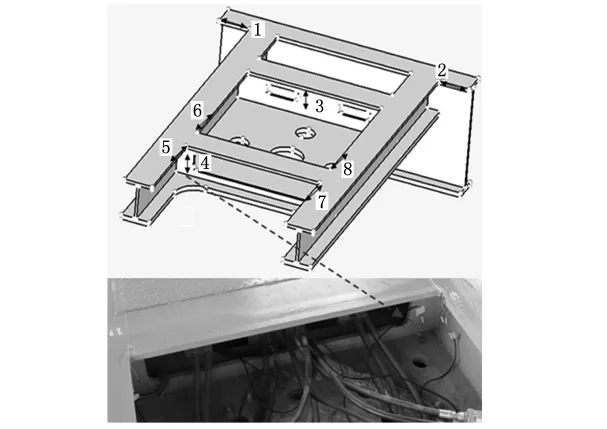
图4 应力试验点位置

试验结果表明，行驶中的车辆应力值相对静止时分布有所不同，最危险的部位与静止时一致，数值上有所增加。有限元仿真结果与应力试验结果对比如表1所示。结果表明，仿真与动态试验误差不大于14.8%，可认为有限元模型是有效的。

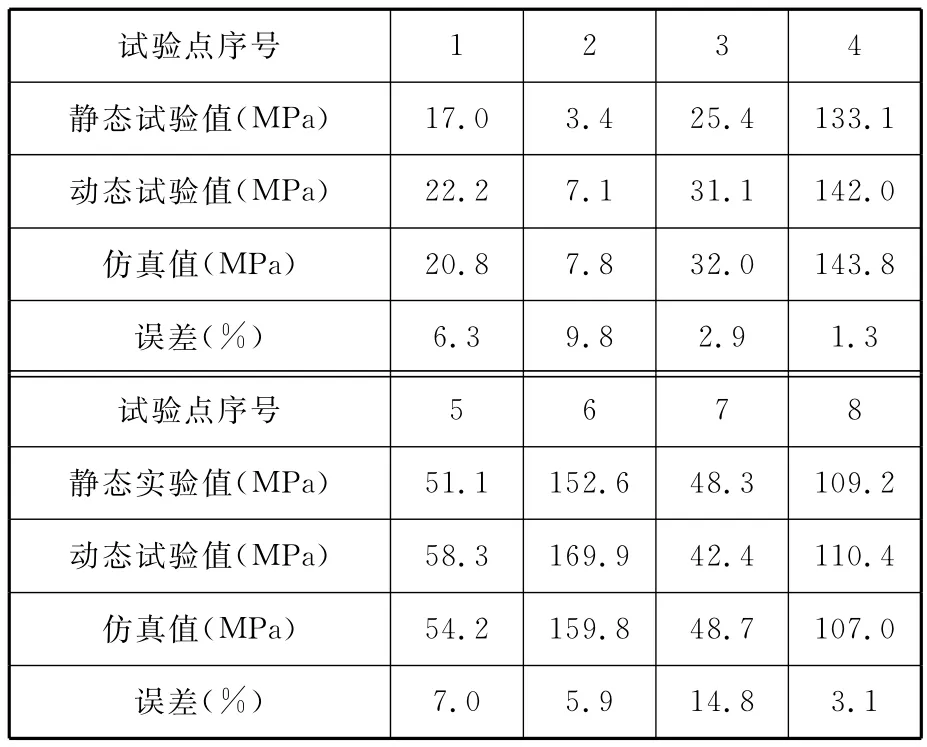
表1 试验值与仿真值及其误差

据文献［6］可知，圆弧与直角边过渡处经常发生应力集中现象。大量文献探讨了关于薄板切口的应力集中系数，但大多属于理论探索，其对矩形薄板的结构形式及受力有很多限制［7－9］。为此本文取敏感部位的参数，即腹板开孔孔长、宽及倒圆半径为不确定变量，以此更有效地避免应力集中现象，为优化提供重要参考。

2 车架的响应面模型

2.1 二次回归响应面法的思路

响应面法的基本思想是用形式已知的简单函数，通过一系列确定性试验，来构造隐式极限状态函数的解析表达式，再通过合理的选取试验点和迭代策略，来保证多项式函数能够在概率上收敛于真实的隐式极限状态函数。本质上来说，该方法是数学方法与统计方法相结合的产物［10］。通常，响应面函数中考查的因素间关系是未知的，进行二次回归设计可以满足一般非线性问题的基本要求。组合设计既能全面满足试验要求，又能充分利用信息［11］。

为满足以上要求，本文选择二次回归正交组合设计为试验方案，它是在自变量空间中选择几种类型的点组合成试验计划，以确定响应面函数的显示表达式。该方案的基本步骤为：

（1）定义设计变量和响应变量；

（2）确定设计变量变化范围并进行因素编码；

（3）选用相应的组合设计进行试验，获得其响应值；

（4）确定回归函数的系数。

2.2 车架响应面模型

为获得腹板处最大应力值与腹板尺寸参数间的显式函数表达式，运用二次回归正交组合设计方法，拟合其回归数学模型表达式：

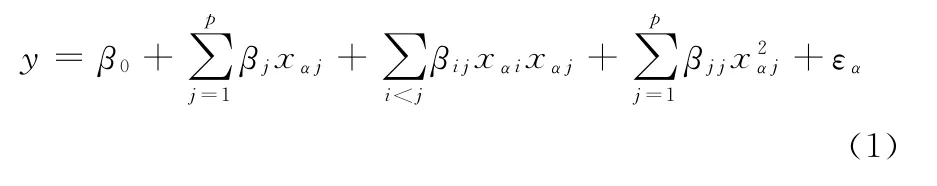
式中，β0、βj、βij、βjj、εα为待定系数；y为函数；xαi、xαj为自变量。

编制试验方案，结合有限元分析求解系数值。首先选取设计变量为腹板开孔处孔长、宽及倒圆半径，记为z01、z02、z03（图5），设计变量总数记为P。根据结构限制与设计要求，设计变量的取值范围如表2所示，对设计变量进行编码，用xj表示水平，zj表示因素，其对应关系如表3所示。其中，z2j、z1j为对应第j个因素的上下限，Δj可通过公式Δj＝（z2j－z1j）／（2r）求得，其中r为臂长，可由表查得［10］，这样就完成了设计变量的编码。对表3中3因素5水平进行试验，通过有限元软件ANSYS求解其响应值，即腹板处最大应力值。 试验号1，即孔长z1为1175.26mm，孔宽z2为193.23mm，倒圆半径z3为34.12mm时，腹板的最大应力如图6所示，最大值为173.716MPa。按照三元二次回归正交设计试验方案，并计算响应值，如表4所示。

图5 选作设计变量的腹板参数

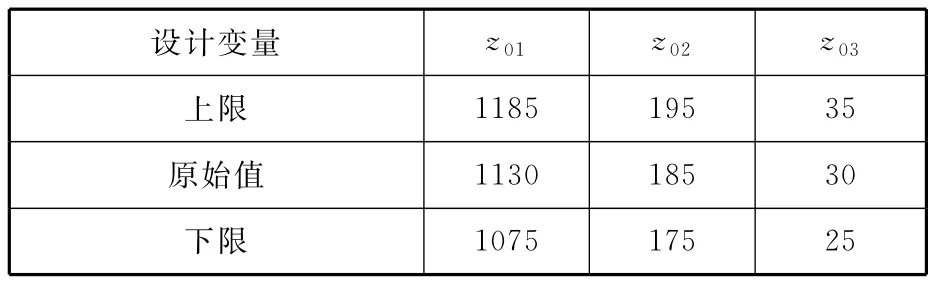
表2 设计变量取值范围mm

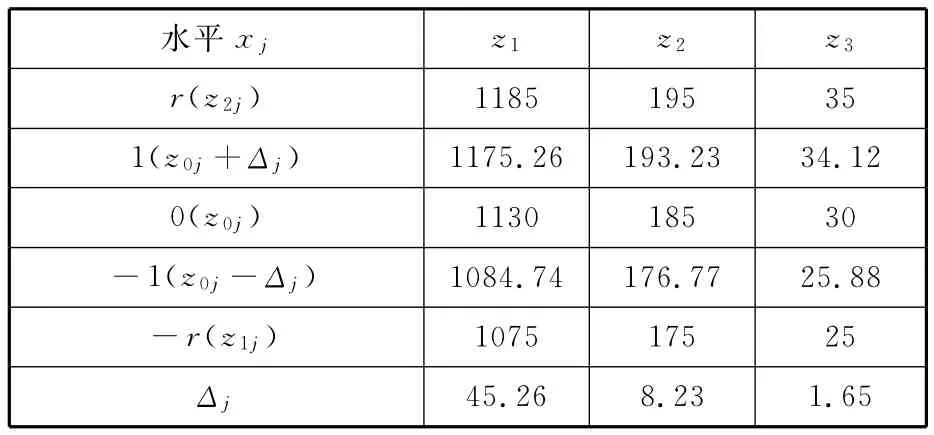
表3 设计变量编码表 mm

图6 试验号1的腹板应力云图

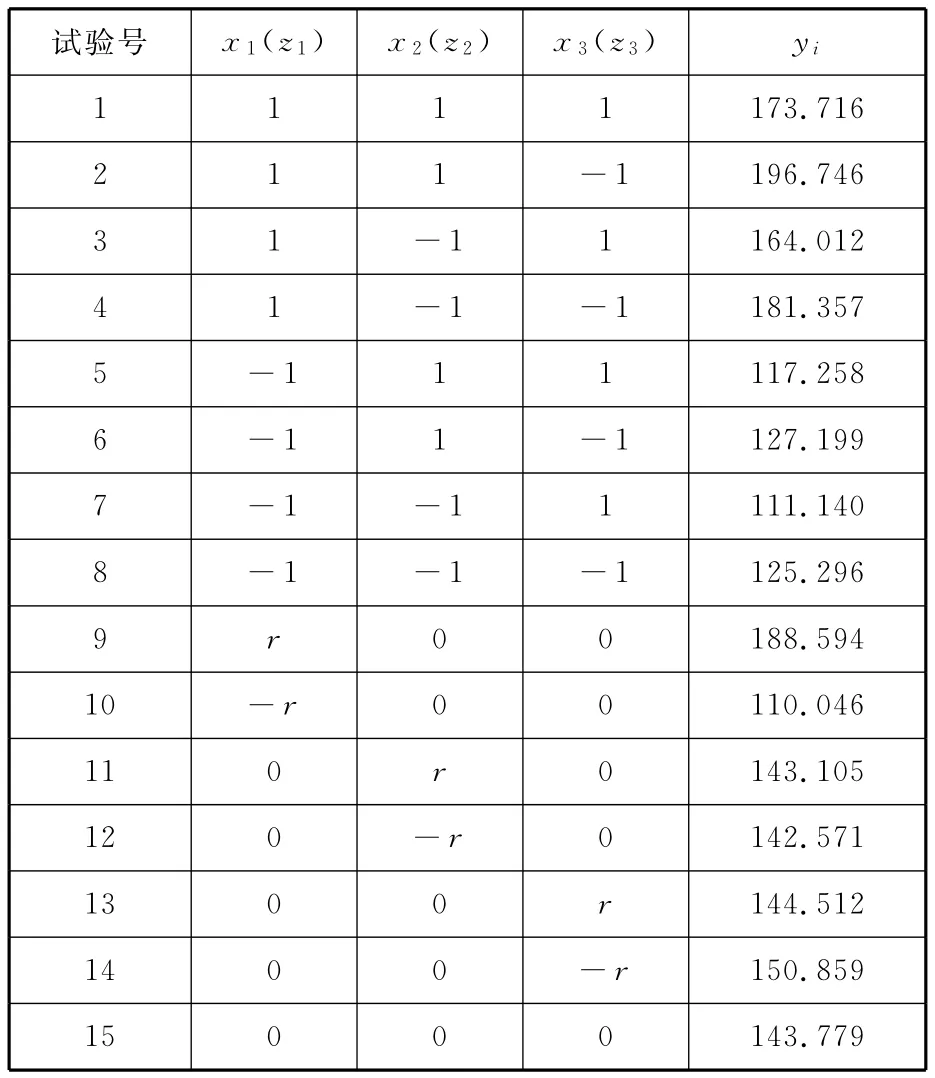
表4 车架正交组合设计试验方案

根据上述试验方案计算式（1）的各项系数，获得如下回归方程：

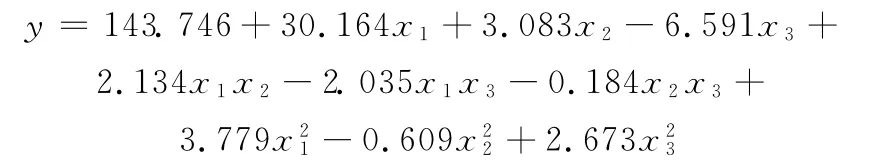
经F检验显示，回归方程达0.01显著，表明方程拟合很好，达极显著水平，可以认为是最优回归方程［7］，即车架腹板最大应力值回归函数。

3 车架结构优化

通过二次组合回归设计得出腹板最大应力值与腹板尺寸的关系式后，可调用MATLAB优化工具箱提供的fimincon函数进行非线性优化求解。

以腹板孔长、宽和倒圆半径为设计变量，腹板质量最小为优化目标，各设计变量的上下限及最大应力值小于许用应力为约束条件，建立如下优化模型：

其中，y0为许用应力，Q345的屈服极限为345MPa，取安全系数为2，许用应力值为172.5MPa。y（z1，z2，z3）函数即由前面的回归公式将设计变量z1，z2，z3替换编码x1，x2，x3得到。由于密度和厚度为固定值，将质量最小简化为横截面积S最小，其计算公式为

通过MATLAB的非线性优化函数fimincon计算上述模型的最优值和对应的设计变量取值。优化结果为：当孔长为1123mm，孔宽为195mm，孔倒圆半径为26mm时，得最小截面面积为250 540mm2，使腹板质量减小6.92%，此时腹板处最大应力为171.94MPa。

4 可靠性分析

在功能函数形式已知的情况下，可通过一次二阶矩法计算结构的可靠度。工程结构可靠度的分析具有大量的不确定性，结构本身的不确定性包括构件材料的性能、截面几何参数和计算模型的精度等［12］，本文以腹板截面几何参数zj为随机变量，根据可靠性理论知识，用随机向量表示结构中的不确定参数为功能函数，那么即为极限状态方程，可靠度指标β表示为

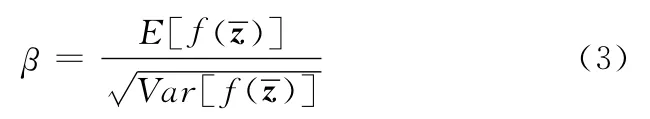
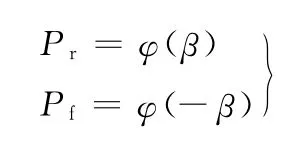
其中，Pr为可靠概率，Pf为失效概率。由可靠度指标的几何意义可知，在极限状态曲面上离原点最近的点称为验算点，其对应的最短距离即为β，那么，可靠度指标可以归结为优化约束模型［13］：

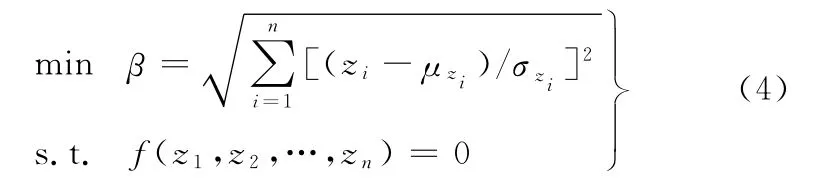
上述优化模型也可由MATLAB非线性优化函数fimincon进行编译求解。最后将优化结果如下（尺寸取整）：孔长为1132mm，孔宽为185mm，孔倒圆半径为26mm时，可靠度指标为3.5111，失效概率为2.2311×10－4，可认为结构可靠。此时腹板的截面积为260 570mm2，腹板质量减轻了3.20%，最大应力值为166.145MPa。

通过上述两种优化模型的求解可知：以许用应力为约束条件的轻量化设计使得腹板质量下降了6.92%，此时最大应力值为171.945MPa；通过可靠度分析获得的腹板参数使得腹板质量下降了3.20%，并取得最大应力值为166.145MPa（表5）。上述两种模型都是在满足结构强度要求的前提下，对部件尺寸参数的优化，不同之处在于前者是以质量最小为优化目标，并在优化过程中把参数都看作确定量；而后者以可靠度为目标，可靠性设计本身考虑随机因素的影响。由优化结果可见后者相对安全，保证了构件的可靠度，但这是以材料体积为代价的，所以在一般情况下可采用轻量化的设计减少材料费用，在需要高可靠度的情况下可采用后者来保证结构安全性。

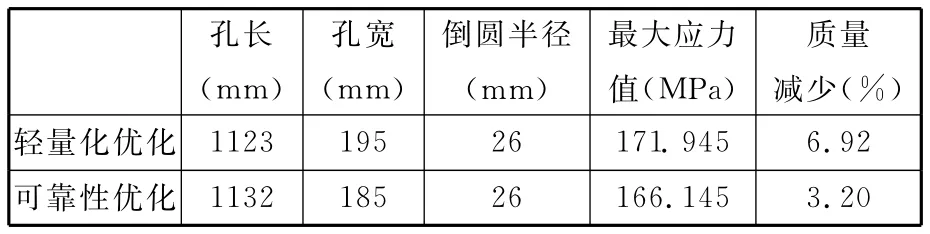
表5 两种优化方法结果对比

5 结论

（1）使用ANSYS软件建立了1／4车架结构的参数化有限元模型，与试验结果进行对比，证明了有限元模型的有效性。利用分析结果，拟定腹板结构尺寸为敏感参数作为优化的设计变量。

（2）通过二次正交组合设计的方法获得了车架腹板处最大应力值的近似表达式，经F检验该式达显著水平，可以认为是最优回归方程。

（3）利用MATLAB的优化工具箱，使用非线性优化函数fimincon对车架腹板结构分布进行了轻量化设计和可靠性分析。前者优化使得车架结构更轻，更充分地利用了材料；而后者更注重车架结构安全可靠，可为平板车车架结构的设计提供一定参考。

［1］Kaymaz I，McMahon C A.A Response Surface Method Based on Weighted Regression for Structural Reliability Analysis［J］.Proabilistic Engineering Mechanics，2005，20：11－17.

［2］Wong S M，Hobbs R E，Onof C.An Adaptive Response Surface Method for Reliability Analysis of Structures with Multiple Loading Sequences［J］.Structural Safety，2005，27：287－308.

［3］Knill D L，Giunta A A，Baker C A，et al.Response Surface Models Combining Linear and Euler Aerodynamics for Supersonic Transport Design［J］.Journal of Aircraft，1999，36（1）：75－86.

［4］赵洁，吕震宙.机械可靠性分析的响应面法研究［D］.西安：西北工业大学，2006.

［5］陈梁胜，归正.组合挂车液压悬架动载荷分析［D］.上海：同济大学，2007.

［6］航空工业部科学技术委员会.应力集中系数手册［M］.北京：高等教育出版社，1990.

［7］郑建校，张义民，原思聪.具有局部应力集中的机械零件结构可靠性分析［J］.机械设计与制造，2011（7）：260－262.Zheng Jianxiao，Zhang Yimin，Yuan Sicong.Structure Reliability Analysis for Mechanical Components with Local Stress Concentrations Machinery［J］.Design ＆ Manufacture，2011（7）：260－262.

［8］郁大照，陈跃良，胡家林，等.降低含多孔带板应力集中的有限元研究［J］.海军航空工程学院学报，2005，20（5）：543－546.Yu Dazhao，Chen Yueliang，Hu Jialin，et al.Finite Element Study on Minimization of Stress Concentration Factors of Finite Plate with Multi－holes［J］.Journal of Naval Aeronautical Engineer Institute，2005，20（5）：543－546.

［9］罗林，向宇，王启智.拉伸偏心椭圆孔板的应力集中系数表达式［J］.应用数学和力学，2012，33（1）：113－124.Luo Lin，Xiang Yu，Wang Qizhi.Stress Conentration Factor Expression for a Tension Strip with an Elliptical Hole［J］.Applied Mathematics and Mechanics，2012，33（1）：113－124.

［10］贾东升，李国平，白晓辉.基于响应面法的液力耦合器叶轮结构优化设计［J］.煤矿机械，2010，31（12）：3－5.Jia Dongsheng，Li Guoping，Bai Xiaohui.Structural Optimization Design of Impeller of Hydrodynamic Coupling Based on Method of Response Surface［J］.Coal Mine Machinery，2010，31（12）：3－5.

［11］白厚义.回归设计及多元统计分析［M］.南宁：广西科学技术出版社，2003.

［12］高雪梅.工程结构可靠度分析的一次二阶矩法探讨［J］.山西建筑，2009，35（20）：57－58.Gao Xuemei.Discussion on the First－order Second－moment Method of Project Structural Reliability Analysis［J］.Shanxi Architecture，2009，35（20）：57－58.

［13］冷伍明.基础工程可靠度分析与设计理论［M］.长沙：中南大学出版社，2000.