基于数字信号处理的串联重复序列识别方法
2013-09-06赵阳
赵 阳
(太原理工大学,山西 太原 030024)
0 引言
随着许多生物基因组测序工作的完成,大量的重复序列被发现。重复基因序列在生物进化过程中起着非常重要的作用,这些重复序列在病毒和原核生物中很少出现,在真核生物中则大量存在。目前科学证实,人类基因组中大约含有50%以上的重复基因序列[1]。这些串联重复序列可能会与一些转录因子结合位点相互作用改变染色体的结构或者作为蛋白质结合位点与其他蛋白质相结合。由于串联重复序列的多态性,个体间串联重复序列中重复拷贝的个数可能不同,因此一些串联重复序列可以用来研究基因标识、基因图谱、个体识别等[2]。生物学家将重复序列作为研究非编码区的突破口,掌握基因组非编码区规律的重要途径。
2009年HongXia Zhou等人[3]提出了一种基于参数谱估计的串联重复序列识别方法,PSE(Parametric Spectral Estimation)识别法,作者采用了现代频谱估计中的自回归模型(AR Auto-Regressive)作为功率谱估计的模型。通过对该方法的进一步分析,发现该方法在求解基因串联重复序列时还存在不足之处。首先,基因序列的频谱图会出现谱峰分裂现象,不利于观察串联重复序列的重复周期。其次,识别速度有待提高,PSE识别法中采用二进制表示法将基因序列映射成数字序列,导致计算量增大,识别速度不高。最后,模型阶次的确定准则有待改进,阶次的准确与否直接关系到谱估计的分辨率。PSE识别法中根据每一种定阶准则分别求出基因序列的阶次,并根据实验估算出适合该模型的阶次,没有明确指出具体应该如何为模型确定阶次,导致容易出现估计误差。
通过对参数谱估计识别法进行深入研究并结合串联重复序列识别的理论知识,针对该方法存在的不足,本文提出了基于自回归模型的串联重复序列识别方法,对以上不足进行了改进。
1 基于自回归模型的串联重复序列识别
基于参数估计的功率谱估计是现代功率谱估计的重要内容,其目的就是为了改善功率谱估计的频率分辨率。它主要包括自回归模型(AR Auto-Regressive)、滑动平均模型(MA Moving Average)以及自回归滑动平均模型(ARMA Auto-Regressive Moving Average)[4]。
由于AR模型的参数估计只需要解一组线性方程,而ARMA以及MA模型的参数估计通常需要解一组非线性方程,因此求解AR模型参数估计的过程会相对容易一些。基于AR模型的功率谱估计是最常用的一种参数估计频谱分析方法,本文将采用AR模型识别基因序列中的串联重复序列。其功率谱可表示为:

1.1 基因序列的数字映射
基因序列是由四种碱基(A、T、G、C)组成的字符串序列。为了在DNA序列分析中使用数字信号处理的方法,首先需要将DNA序列中的四个碱基分别映射成数字。本文根据各个碱基的EIIP[5]值将DNA序列映射成为一条数字序列。碱基的EIIP是碱基的物理属性,表示其价电子的平均能量,可唯一表示一种碱基。该映射法可将一条基因序列惟一的映射为一条数字序列,相比二进制映射法,其计算量减少了3/4。各碱基的EIIP值如表1所示。

表1 各碱基的EIIP值
1.2 基因序列的去直流化
在求数字基因序列的谱估计时,为了避免基因信号中直
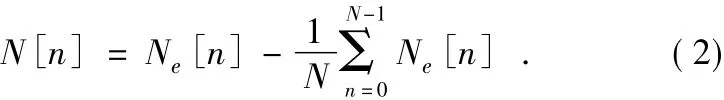
其中Ne[n]为原数字序列,N[n]为去直流化的基因数字序列,并最终采用N[n]进行阶次估计及参数估计。
1.3 自回归模型阶次确定
模型阶数p是一个非常重要的参数,当阶数选择过小时,会导致相应的AR模型的极值点不够精确,表现为谱峰较少,频谱较为平滑,频谱分辨率下降;而当阶数选择过大时,谱估计值的分辨率虽然会有所提高,但是会产生虚假的谱峰,导致其统计特性的不稳定。因此我们需要为模型确定一个合适的阶次,既要保证谱估计的分辨率较高,又不至于出现虚假谱峰。下面是几种阶数估计准则。

(1)最终预测误差准则(FPE)流信号的干扰,这里需要对基因数字信号进行处理,将每一个数字信号分别减去整个数字信号序列的平均值得到一个新的数字序列:
(2)Akaike信息准则(AIC)


上述三式中其中L为数据长度,p为模型阶数,ρp表示p阶AR模型的预测误差功率估计值。
根据已有理论可知,各准则函数取得最小值时的阶次p即为AR模型阶次。每一种定阶准则都有其优缺点,并且对于同一输入采用不同的准则得到的阶数可能不同。为了减小因为阶次选择不准确导致的谱估计误差,本文将三种准则所确定阶次的平均值作为模型的阶次,经过反复试验发现,通过该方法确定的阶次较为准确,得到的谱估计结果能够满足串联重复序列识别所需要的分辨率。
1.4 AR模型的参数估计
由(1)式可知,只要得到该模型的参数估计{a(1),a(2),LL,a(p)}及噪声方差σ2就可以得到该模型的功率谱密度。常用的模型参数估计方法主要有尤克-沃勒(Yule-Walker)算法,Burg算法,协方差算法以及改进的协方差算法。本文将采用改进的协方差算法作为AR模型参数估计的方法。改进的协方差方法克服了Burg算法的缺点,采用该方法能够有效地避免谱线分裂现象的出现[6]。
在得到的功率谱密度图中横坐标表示频率,纵坐标表示功率谱密度值。当一个基因序列中包含周期为n的串联重复序列拷贝时,在功率谱密度图中对应频率为ω=2π/n处将会出现一个显著的波峰。在得到基因数字序列的谱估计之后根据信噪比的设置从功率谱密度图中选择出对研究有意义的波峰,此时便可得到串联重复序列拷贝在基因序列中出现的频率,进而得到串联重复序列拷贝的周期即拷贝
(3)贝叶斯信息准则(BIC)长度。
在得到的功率谱密度图中能够很好地显示基因序列中的频率信息,即图中波峰出现的地方对应的频率就是串联重复序列拷贝在基因序列中出现的频率。但是由于在功率谱密度图中可能会出现若干个波峰,并且有些波峰并不能被认为是对识别串联重复序列有意义的信息,因此需要有针对性地选择一些对识别串联重复序列有用的波峰。本文采用信噪比来确定每一个波峰的重要性,即当S(k)/Sm>S/N成立时便认为功率谱密度图中的波峰是有意义的。研究表明,当信噪比设置为4时,能更好地识别串联重复序列的位置信息,因此这里将信噪比设置为4。根据信噪比确定出在功率谱密度图中有意义的波峰,则波峰对应的频率即为串联重复序列拷贝在基因序列中出现的频率,求其倒数便可得到串联重复序列拷贝的周期。
1.5 串联重复序列定位
在分析过基因序列的功率谱密度图之后,得到了序列中存在的串联重复序列拷贝的长度,这里将采用短时傅里叶变换对序列进行分析,便可得到串联重复序列在基因序列中出现的位置[7]。序列Ne[n]的短时傅里叶变换:

其中k=0,1,L,M-1。在求基因序列的短时傅里叶变换时需要根据信号的特点选择适合的窗函数以及窗口大小。适合的窗函数以及窗口大小能够使得频谱更加精确,分辨率更高。
2 实验及结果分析
为了验证本文方法的正确性及有效性,本文从美国国家生物技术中心(NCBI)维护的基因数据库GenBank[8]中提取了若干条基因序列进行分析。本文将以序列Y-27H39为例进行详细实验过程分析。
2.1 实验过程
首先将序列Y-27H39根据各碱基的EIIP值映射为数字序列。然后采用基于AR模型的谱估计法对数字序列进行谱估计。观察序列中串联重复序列拷贝出现的频率。
在求数字序列的谱估计时,需要先确定该数字序列的阶次。如图1所示分别为采用FPE、AIC、BIC三种定阶准则估计的阶次结果。从图中可以观察到由三种定阶准则确定的阶次分别为:22,22,9。根据上文中关于模型阶次的分析,这里将采用的阶次为18。
其次,结合已确定的阶次利用参数谱估计方法进行基因序列的谱估计。为了对比方便,我们分别采用已有的PSE识别法以及新提出的方法分别求出了序列Y-27H39的谱估计,如图2及图3所示。从二者的对比可以看出,本文提出的方法避免了PSE识别法中存在的谱峰分裂现象。
最后通过对该序列求短时傅里叶变换便可得到该序列中串联重复序列出现的位置,如图4所示,矩形中标注的部分便是序列Y-27H39中串联重复序列出现的位置。
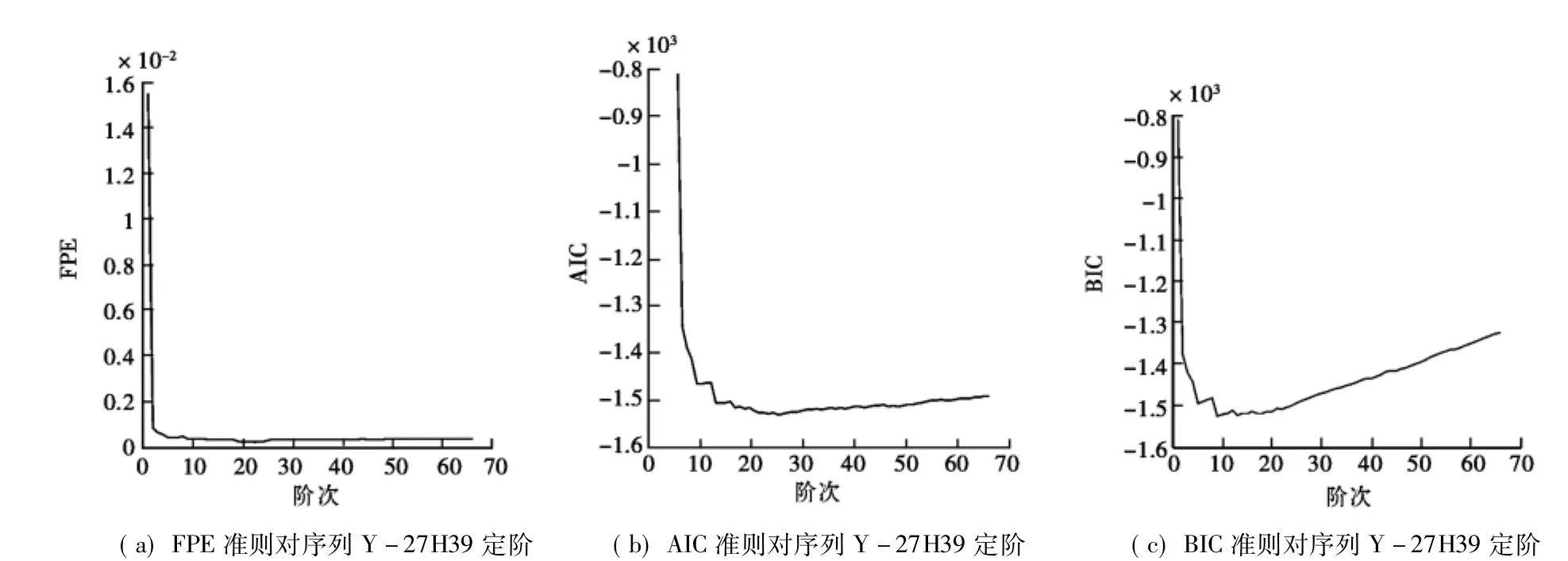
图1 采用FPE、AIC以及BIC准则分别对序列Y-27H39定阶

图2 PSE识别法得到的

图3 序列Y-27H39的谱估计
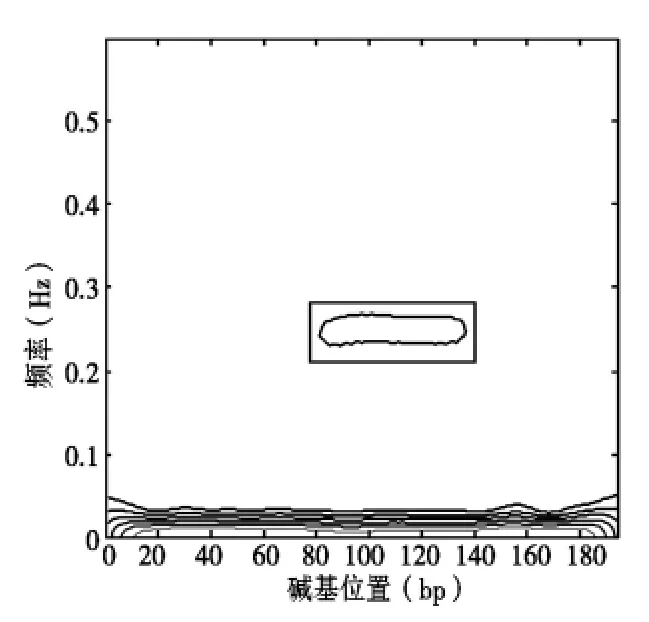
图4 序列Y-27H39的短时傅里叶变换
但是PSE识别方法采用了二进制表示法进行基因序列的数字映射,在进行谱估计时将一条基因序列映射成为四条数字序列,即针对每类碱基各得到一条数字序列,需要分别对得到的四条序列求四次谱估计才可以得到最终的谱估计,计算量较大。本文提出的方法可唯一地将一条基因序列映射成一条数字序列,并针对该序列进行谱估计,计算量相对前者减少了75%,由于基因序列数据量较大,因此计算量是进行基因序列分析必须考虑的问题之一。另外,从图2及图3的对比可以看出,本文提出的方法解决了PSE识别法中存在的谱峰分裂现象,使得得出的串联重复序列出现频率更加精确,便于进一步进行串联重复序列位置分析。
2.2 实验结果分析
从图2中的波峰处可以看到谱峰出现了分裂现象,但是仍能模糊地判断出此处波峰对应的频率大约为F=0.25 Hz,这是因为该序列是一个短基因序列,只有194个碱基。当序列长度较长或者序列中包含的串联重复拷贝较多时就很难准确地断定波峰处对应的频率究竟应该是多少,这样就对进一步识别串联重复序列出现的位置带来了困难。出现谱峰分裂现象的主要原因是PSE识别法中采用的模型参数估计方法不当。PSE识别法中采用了Burg算法作为参数估计的方法,不能保证对所有的基因序列都能得到其准确的功率谱估计。
观察图3可以发现并没有出现谱峰分裂现象,从图中波峰位置可以清楚地判断该序列中串联重复序列出现的频率为0.25 Hz,进而可以判断该序列中串联重复序列出现的周期为4,即串联重复拷贝长度为4 bp。
表2中列出了采用本文提出的识别方法对序列Y-27H39进行分析,得到的串联重复序列位置,并与PSE识别法以及GenBank中标注的位置进行了对比。从表2中可以看出,两种方法均能较准确地定位出串联重复序列的位置。
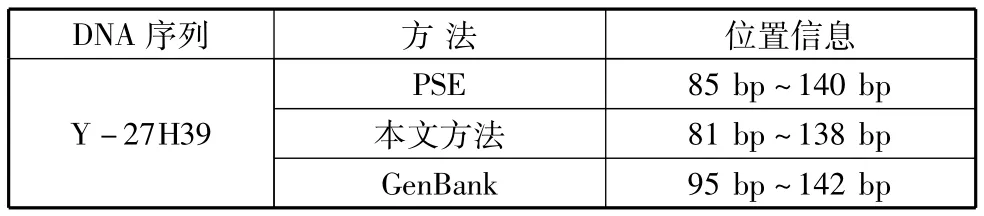
表2 定位精度比较
2 结论
基于参数谱估计对已有的PSE识别方法进行了改进,采用碱基的EIIP作为序列数字映射的依据,大大减小了谱估计的计算量;并对参数估计方法进行了改进,采用改进的协方差方法作为参数估计方法,有效避免了可能会出现的谱峰分裂现象。今后将对识别的精度作进一步的研究。
[1]Lander E S,Linton L M,Birren B,et al.Initial Sequencing and Analysis of the Human Genome[J].Nature,2001,409:860-921.
[2]Naruse K,Tanaka M,Mita K,et al.A Medaka Gene Map:the Trace of Ancestral Vertebrate Proto-chromosomes Revealed by Comparative Gene Mapping[J].Genome Research,2004,14(5):820-828.
[3]Zhou H X,Du L P,Yan H.Detection of Tandem Repeats in DNA Sequences Based on Parametric Spectral Estimation[J].IEEE Transactions on Information Technology in Biomedicine,2009,13(5):747-755.
[4]张善文,雷英杰,冯有前.Matlab在时间序列分析中的应用[M].西安:西安电子科技大学出版社,2007:130-139.
[5]Irena Cosic.Macromolecular Bioactivity:Is It Resonant Interaction Between Macromolecules–Theory and Applications[J].IEEE Transactions on Biomedical Engineering,1994,41(12):1101-1114.
[6]Akhtar M,Ambikairajah E,Epps J.Comprehensive Autoregressive Modeling for Classification of Genomic Sequence[C].Proceedings of the IEEE 6th International Conference on Information,Communications& Signal Processing,Singapore,2007:1-5.
[7]胡广书.现代信号处理教程[M].北京:清华大学出版社,2006:52-61.
[8]GenBank[OL]http://www.ncbi.nlm.nih.gov/genbank/2011.
