基于Hopfield神经网络的中考达线等级预测模型

2013-09-06李静

山西电子技术 2013年1期

李静

（忻州师范学院计算机科学与技术系，山西忻州 034000）

中考是目前我国青少年成长的必经之路，中考成绩的高低不仅关系到学生自身的成长，关系到家庭、学校的未来发展，对国民素质的整体提高也有着很大的影响。因此，准确预测中考成绩具有重要意义。而影响中考成绩的因素是多方面的，除了学习成绩，学生的身体素质、心理素质等不可预知的因素也发挥着一定作用。这样，如何有效预测中考成绩，以便于学生、家长、学校在考前做出合理的规划，已成为急待解决的问题。

1 Hopfield神经网络

1.1 网络的结构［1，2］

Hopfield神经网络是典型的反馈型网络，具有单层、全互连结构。根据网络激励函数的不同，又分为离散型和连续型两种，本文用离散型Hopfield神经网络（DHNN）来建立中考成绩预测模型。

在DHNN中，采用二值神经元，神经元的输出只取离散值1和-1。设网络中有n个神经元，其中任意神经元i与j间的互连权值为ωij，神经元i在t时刻的输入用ui（t）表示，输出用vi（t）表示，则有:

式（1）中，bi表示神经元i的偏差，即其他外部输入。

若激励函数取符号函数Sgn（t），有:

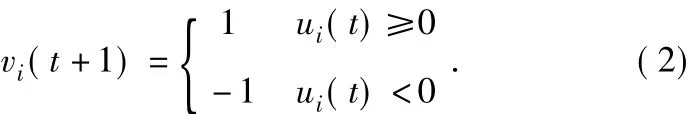
在某一时刻，网络通过对输入值与连接权值的乘积求累加和，并经过非线性激励函数处理后产生输出信息。取激励函数为简单的符号函数，若输出大于0，则神经元的输出取值为1;小于0，则神经元的输出取值为-1。

1.2 网络的联想记忆功能［3］

DHNN的工作过程是神经元状态的演化过程，即给定网络一组初始值时，网络自动按照“能量函数”减小的方向进行演化，最终达到稳定的平衡状态。DHNN模拟了生物神经网络的联想记忆功能。在存储记忆阶段，通过设计或训练网络的权值，在系统的平衡状态存储记忆模式，若将网络最终演化的平衡状态看作网络的记忆，则从初态向这个平衡态流动的过程，就是寻找该记忆的过程。在联想回忆阶段，首先给定输入模式，网络按动力学方式运行达到稳定状态，即收敛于若干个平衡点，最后回忆起已记忆的模式。

在中考成绩预测模型的设计过程中，将达线等级对应的各最佳影响因素值设置为DHNN的平衡点，对网络进行训练，训练出的记忆模式与标准的中考达线等级相对应，这是网络的存储记忆过程;当有待预测的中考成绩影响因素输入时，DHNN即利用其联系回忆的能力逐渐趋近于网络的某个平衡点，当状态不再改变时，即网络联想回忆出了离它“最近”的一种记忆模式，此时记忆模式中存储的便是待预测的中考成绩达线等级，最终实现用学生的平时成绩预测其中考达线等级的目的。

2 基于DNHH中考成绩预测模型

2.1 建立中考成绩预测指标体系

影响学生中考成绩的因素很多，本文中以学习成绩、身体素质和心理素质作为预测指标。其中，学习成绩以学生的七门中考科目来衡量，分别是语文、数学、英语、物理、化学、思想品德和历史，各门课程的成绩取中考前7次月考的平均值;身体素质的评价主要以学生平时的体育成绩为依据;学生心理素质的考量涉及到诸多不可预知的因素，文中取值主要来自学生心理课成绩及班主任老师对该生的综合评价。对中考达线等级的评价分为三等，一等为达重点中学线，用Ⅰ来表示;二等为达普通中学线，用Ⅱ表示;三等为不达线，用Ⅲ表示。

2.2 数据准备

本文以忻州师范学院附属中学106班的学生作为实验样本，经预处理后，选取容量为60的学生成绩进行网络训练，部分样本数据如表1所示。

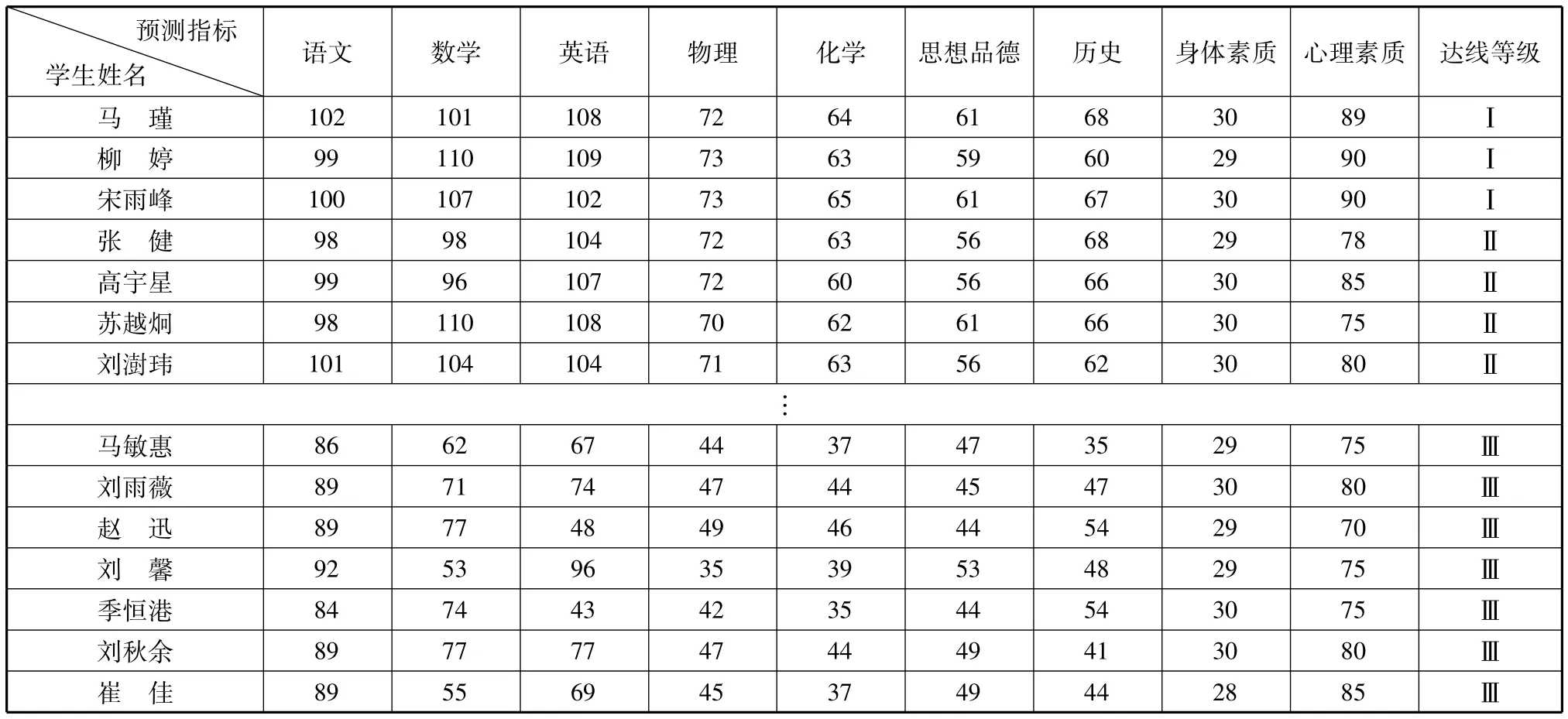
表1 60名学生的中考成绩预测指标及实际达线等级

2.3 建立中考成绩预测模型

计算样本中达线等级对应的各影响因素的平均值作为预测指标的最佳值，即DHNN的平衡点，结果如表2所示。

表2 达线等级对应的预测指标最佳值

以中考达线等级（3个）为横轴，各项预测指标（9个）为纵轴，构成3*9，共27个神经元的网络。由于DHNN神经元的状态只有1和-1两种情况，所以将预测指标映射为神经元状态时，需要将其进行编码。编码规则为:当最接近且大于或等于某个等级的最佳指标值时，对应的神经元状态设为“1”，其余的设为“-1”。用3个9*3的矩阵 a1，a2，a3分别表示3个达线等级对应预测指标的最佳值，矩阵a1如下。

a1=［1-1-1;1-1-1;1-1-1;1-1-1;1-1-1;1-1-1;1-1-1;1-1-1;1-1-1;］

如前所述计算方法，收集待预测的10个学生成绩如表3所列。

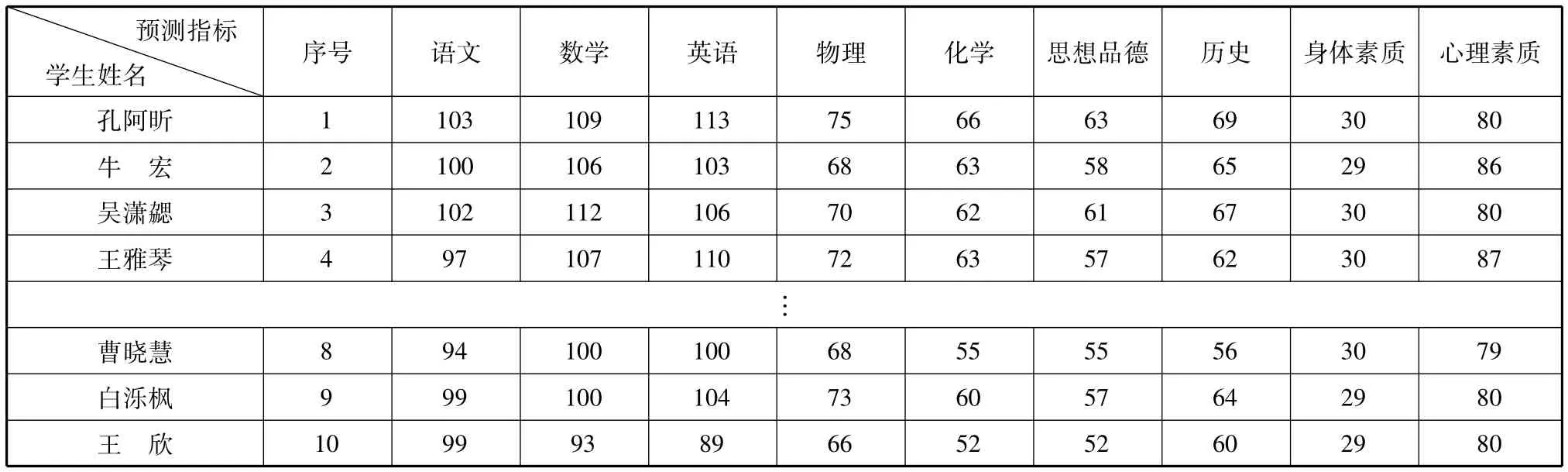
表3 待预测的部分学生成绩

按照编码规则，将各项待预测指标与最佳值进行比较，生成编码矩阵，此处只列出学生孔阿昕的编码矩阵b1如下。

b1=［1-1-1;1-1-1;1-1-1;1-1-1;1-1-1;1-1-1;1-1-1;1-1-1;-1-1 1］

3 预测模型的MATLAB实现［4］

3.1 创建Hopfield神经网络［5］

本文采用MATLAB7.0神经网络工具箱中的net=newhop（T）函数创建离散型Hopfield神经网络，其中T为训练样本，在本文中，T是由3个9*3的矩阵构成;net为生成的神经网络，具有在T中向量上稳定的点;网络的传递函数采用对称饱和型函数satlins（）;网络的权值由newhop函数默认的正交化法自动修正。