基于实体变形的六面体网格生成方法研究

王 帅

（北京航空航天大学 机械工程及自动化学院，北京 100191）

0 引言

常用的六面体网格生成方法有映射法［1］、扫掠法［2］、四面体转换法［3］、基于栅格法［4］、波前推进法［5］等。对于结构复杂的模型，单独使用上述几种方法都无法获得整体质量较好的六面体网格。近年来基于实体变形技术的六面体网格生成方法成为研究热点，但这种方法需要先对多方体模型进行网格划分，再将整套网格映射回原始模型，如此一来需要生成两套网格数据，降低了网格的生成效率。

针对这一问题，本文提出一种利用节点填充的方式直接在原始模型中生成结构化六面体网格的方法：利用实体变形技术得到多方体模型后，不对变形多方体做实际剖分，仅通过线性规划得到各顶点的网格信息，利用顶点信息，直接在原始模型中经过边节点填充、面节点填充、体节点填充生成结构化六面体网格。

1 基于实体变形的网格生成技术

Y．Su［6］利用实体变形技术将原始模型变换为各边与坐标系平行的识别模型（多方体模型，polycube），用栅格法对识别模型划分六面体网格，然后将识别模型网格映射回原始模型，过程如图1所示。这种方法可以生成质量较高的结构化网格，避免了体分解，对拓扑结构为类多方体的复杂结构有良好的剖分效果。但这种方法需要先对多方体模型进行网格划分，再将整套网格映射回原始模型，如此一来需要生成两套网格数据，降低了网格的生成效率。

2 节点填充法

对于结构复杂的模型，很难得到原始模型顶点的网格坐标；经过实体变形后的多方体模型，利用基于线性规划的子映射法［7］，可以较容易求得多方体模型各顶点的网格坐标（i，j，k）；映射回原始模型，即可得到原始模型各顶点的网格信息，即实际坐标值与网格坐标值的对应关系。

图1 基于实体变形的网格生成技术

本文利用模型顶点的网格坐标信息，通过边节点填充、面节点填充、体节点填充的方式，直接在原始模型中生成各网格节点，过程如图2所示。具体步骤如下：

（1）边节点填充：在原始模型的每条边上，利用顶点的网格坐标值得到该边的节点个数，在该边按等弧长创建节点，完成边节点填充。

（2）面节点填充：在原始模型的每张面上，得到面内未知节点的网格坐标值，利用8节点等参元模型对所有面内未知节点构建线性方程组，求解方程组即可得到面内各节点的实际坐标值，完成面节点填充。

（3）体节点填充：根据所有已知的面节点，得到体内未知节点的网格坐标值，利用20节点等参元模型对所有体内未知节点构建线性方程组，求解方程组即可得到体内节点的实际坐标值，完成体节点填充。

图2 节点填充法生成六面体网格的过程

2．1 数据结构模型

2．1．1 二维节点数据结构

在二维面节点填充算法实现过程中，每个二维节点包含的数据为 P（i，j）＝（x，y，flag，edgeTag）。其中，（i，j）为二维节点的网格坐标，x，y为二维节点的实际坐标，flag为该节点与形成该面的多边形的位置关系（－1：该节点不在多边形内；0：该节点为多边形边界点；1：该节点在多边形内），edgeTag为该节点所属边的编号。

图3为二维网格节点示意图。

图3 二维网格节点示意图

在填充边节点时，将各节点所在边的编号存入P（i，j）→edgeTag中（记为edgeTag（i，j），下同），并将该节点的flag值改为0（flag（i，j）＝0），表示该节点为边界节点。判断面内节点，将其flag值改为1。

2．1．2 三维节点数据结构

与二维节点类似，每个三维节点包含的数据为P（i，j，k）＝（x，y，z，flag，faceTag）。其中，（i，j，k）为三维节点的网格坐标，x，y，z为三维节点的实际坐标，flag为该节点与模型的位置关系（－1：该节点在模型体外，0：该节点为模型面上的点，1：该节点为体内点），faceTag为该节点所属面的面编号（若该节点非模型面上点，其值为－1）。

在填充面节点时，将各节点所在面的编号存入P（i，j，k）→faceTag中（记为faceTag（i，j，k），下同），并将该节点的flag值改为0（flag（i，j，k）＝0），表示该节点为面节点。判断体内节点，将其flag值改为1。

图4为三维网格节点示意图。

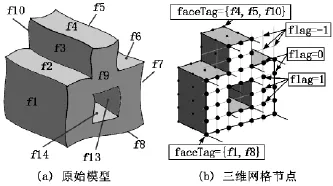
图4 三维网格节点示意图

2．2 基于等参元的线性方程组

在获得所有边界节点的实际坐标以及内部节点的网格坐标后，可以利用等参元模型对每一个内部节点列出实际坐标方程，组成线性方程组，求解此方程组即可得到所有内部点的实际坐标值。

对于二维面网格，本文利用如图5所示的8节点等参元模型构建坐标方程。为表示中间插值点的实际坐标，可利用8个节点和其对应的二次形函数组成8节点的等参元，推导出相应的坐标方程为：

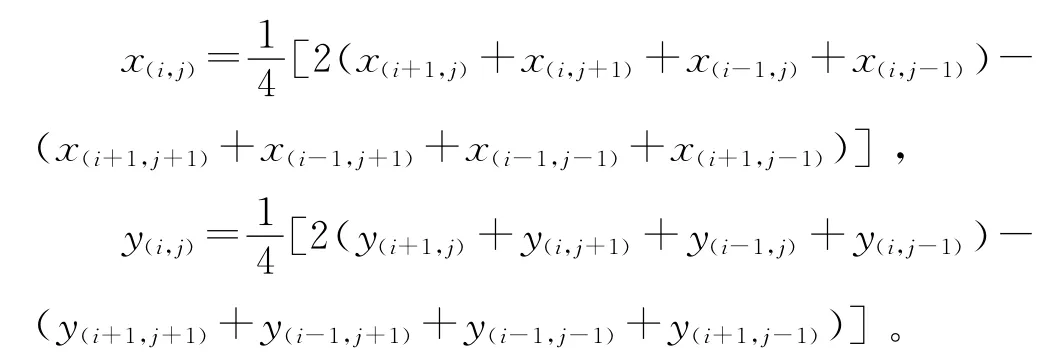
对于结构化网格，当该面所有边界节点的坐标值已知时，对平面内每一个面内待求节点列出以上坐标方程，可以得到两组线性方程组，求解线性方程组即可得到面内各个网格节点的实际坐标（x（i，j），y（i，j））。对于空间参数化曲面，可先在参数平面内利用该方法求得各节点的参数坐标，再通过参数转换得到相应的实际坐标值。

对于三维体节点，本文利用如图6所示的20节点等参元模型，得到每一个体内节点坐标方程为：

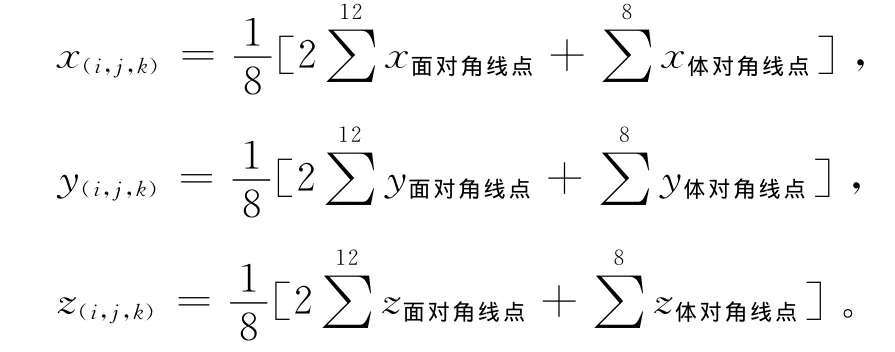
图5 8节点等参元模型

对于结构化网格，当该实体所有面节点已知时，对每一个体内待求节点列出上述的坐标方程，可以得到三组线性方程组，求解线性方程组即可得到体内各个网格节点的实际坐标（x（i，j），y（i，j），z（i，j））。

图6 20节点等参元模型

3 实例验证

根据以上方法，本文以UG NX 3．0为开发平台，利用UG／Open API开发了六面体网格自动剖分模块，对涡轮叶片实体模型的部分结构进行了网格自动剖分，剖分结果如图7所示。

4 结论

本文提出一种基于多方体变形技术的结构化六面体网格生成方法：利用实体变形技术得到多方体模型后，不对变形多方体做实际剖分，仅通过线性规划得到各顶点的网格信息，利用顶点信息，直接在原始模型中经过节点填充生成结构化六面体网格。该方法在保证较高网格质量的前提下，提高了网格生成效率。利用本文方法开发了六面体网格自动生成程序，可以得到整体质量较好的六面体网格。

图7 涡轮叶片肋区网格划分结果

［1］ 王东风，翟建军，陈文亮．基于映射法的六面体网格生成算法［J］．中国制造业信息化，2009，3（5）：25－27．

［2］ 翟建军，乔新宇，丁秋林．基于扫掠法的六面体网格生成算法及实现［J］．南京航空航天大学学报，2007，39（1）：71－74．

［3］ Gregson J，Sheffer A，Zhang E．All－hex mesh generation via volumetric polycube deformation［G］／／Eurographics Symposium on Geometry Processing 2011． USA：Blackwell Publishing，2011：1407－1416．

［4］ 黄丽丽，赵国群，马新武，等．栅格法三维六面体网格自动生成算法与优化［J］．塑性工程学报，2009，16（3）：187－191．

［5］ 俞建威，沈军，卢百平，等．一种新的六面体有限元网格算法［J］．计算机工程与设计，2003，24（9）：22－25．

［6］ Su Y，Lee Ｋ Ｈ ，Kumar ， u．Automatic hexahedral mesh generation using a new grid－based method with geometry and mesh transformation ［J］． Computer Methods in Applied Mechanics and Engineering，2005，194：4071－4096．

［7］ Ruiz－Girones E，Sarrate J．Generation of structured hexahedral meshes in volumes with holes［J］．Finite Elements in Analysis and Design，2010，46：792－804．