结合APO算法的高光谱图像波段选择
2013-09-02王立国魏芳洁
王立国,魏芳洁
(哈尔滨工程大学信息与通信工程学院,150001哈尔滨)
高光谱图像具有波段数多、数据量庞大、数据不确定和小样本分类等特点,而且其波段间相关性强、数据冗余度高,这直接影响了高光谱图像分类的精度和速度[1].因此,在保证地物分类识别率的情况下,减少数据量、节省资源的降维处理是非常有必要的.对高光谱图像进行降维主要有两种途径:特征提取和波段选择.特征提取是将原始高维数据空间进行变换,再取子空间,该方法通常算法复杂、计算量较大,且不利于图像的解译[2].相比之下,波段选择是从高光谱图像所有波段中选出一些最有效的波段以达到降维的目的,不仅有效地去除了冗余特征,避免了“维数祸根”,而且在样本数较少的情况下改善了分类器的性能.
高光谱图像波段选择常常是一个NP难问题[3].一般地,为了获得最优波段子集,即波段子集有较好的性能,必须进行穷举搜索,但这样就会消耗大量的搜索、运算时间,因此不可能得到广泛应用.后来出现的顺序前进法、顺序后退法以及改进的广义顺序前进法、广义顺序后退法等启发式搜索策略,实际上都属于贪心类算法,其搜索计算量较小,在原始数据波段间相关性较小的情况下,能够获得较好的效果.但其存在明显的缺点,比如:某一波段一旦被加入或剔除,则该波段就不能再被剔除或加入,这样容易陷入局部最优.为了克服这些缺陷,后来又出现增减r算法,但其中l和r很难确定.因此,寻找一种计算耗时少、收敛性能好的波段选择方法是亟待解决的问题.智能寻优算法是利用智能寻优搜索策略结合适应度函数来获得次优或近似最优波段子集,并且以降低搜索、运算时间为代价.近些年来,出现了许多将智能寻优算法应用于高光谱图像的波段选择中,并取得了一定的效果.比如,赵冬和赵光恒[4]利用遗传算法进行高光谱图像波段选择;周爽[5]利用蚁群算法进行高光谱图像降维处理;黄睿[6]利用粒子群算法进行高光谱遥感数据特征约简,等等.这些寻优算法中,遗传算法是一种概率搜索寻优算法,可以较好地解决波段选择过程中波段组合数目多、难以遍历的问题,但其收敛速度问题目前仍无法得到满意的解决,即在有限的时间内无法有效收敛.蚁群算法是一种群智能的搜索算法,可以搜索到性能较好的波段组合,但其一般需要较长的搜索时间,而且容易出现停滞现象,产生早熟[7].粒子群算法是一种基于种群迭代的优化算法,其虽然收敛速度较快,但收敛精度不高,而且容易早熟[8].而拟态物理学优化算法是一种新的群体随机搜索算法,受牛顿第二力学定律的启发,通过个体间的虚拟作用力来改变个体的运动速度和位置,使其向较优解的方向移动,最后收敛于全局最优解的附近.并且其具有较好的全局搜索能力,不易陷入局部最优,且具有稳定和快速收敛的特点以及较好的鲁棒性[9].拟态物理学优化算法已经在单、多目标优化问题中得到很好的应用.因此本文提出了结合拟态物理学优化(APO)算法的高光谱图像波段选择,并通过实验验证该算法的有效性.
1 拟态物理学优化算法
拟态物理学(physicomimetics or artificial physics,AP)最早是由Spear等[10]提出的,因受物理力学定律的启发而称其为“拟态”,该算法本质上是模拟了牛顿第二力学定律(F=ma),主要用于解决多机器人系统的分布式控制.王艳和曾建潮[11-12]研究了拟态物理学,并首次将其成功应用于解决优化问题,提出了拟态物理学优化算法(physicomimetics or artificial physics optimization,APO).该算法是一种群体随机搜索算法,其每个个体代表解空间中的1个可行解.每个个体依据自己的惯性以及所受其他个体的作用力合力来调整自己的速度和位置,最后整个群体得到的最优位置就是目前得到的全局最优解,个体的好坏由优化问题的适应度来评价.每个个体根据全局最优、最差适应度和自身适应度不断更新其质量,通过质量的变化影响虚拟力的变化,来更新个体的速度和位置.
APO算法中,设群体规模为n,则第i(i=1,2,…,n)个个体的质量表示为mi,在第k维个体i的速度表示为vi,k,在第k维个体i的位置表示为xi,k.个体的质量不是一个常量,而是一个用户定义的关于其适应度值的函数.个体的适应度值越好,其质量就越大;个体的适应度值越差,其质量就越小.在求解最大化问题时,个体的适应度值越大,表明该个体的适应度值越好,则其质量就越大;在求解最小化问题时,个体的适应度值越小,表明个体的适应度值越好,则其质量就越大.个体i的质量计算如下:
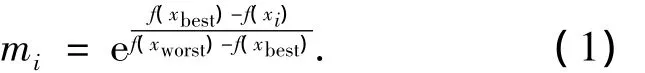
其中:xbest为当前种群中的最优个体;xworst为当前种群中的最差个体;f(xbest)为最优个体的适应度值;f(xworst)为最差个体的适应度值;f(xi)为个体xi的适应度值.从公式可看出,个体质量在(0,1]内变化,个体的适应度值越接近最优解,个体的质量越大,反之,个体的适应度值越接近最差解,个体的质量越小.因此,个体质量的大小是该个体在整个种群中优劣的一个评价.
在第k维上,个体i受个体j的虚拟作用力为Fij,k,其计算如下:
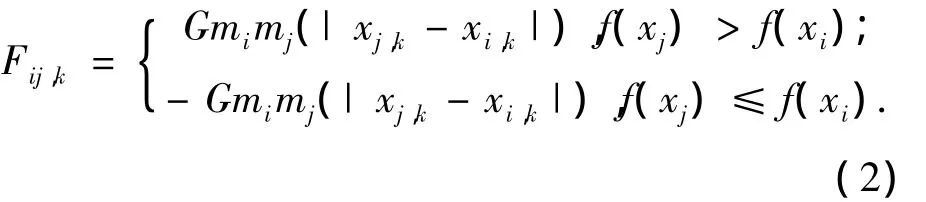
其中∀i≠j&i≠best;G为引力常量;|xj,k-xi,k|为个体j到个体i在第k维上的绝对距离.适应度值好的个体吸引适度值差的个体,适应度值差的个体排斥适应度值好的个体,作用力的方向和大小由式(2)给出.且其他个体不作用于全局最优个体.
在第k维上,个体i(除最优个体外)受到群体中其他所有个体的作用力合力为Fi,k,其计算公式下:
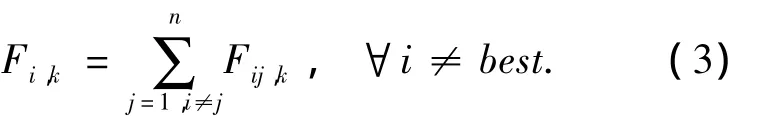
除最优个体外,每个个体在作用力合力的作用下进行运动.在t+1时刻,个体i每一维的速度和位置的更新方程如式(4)和式(5):
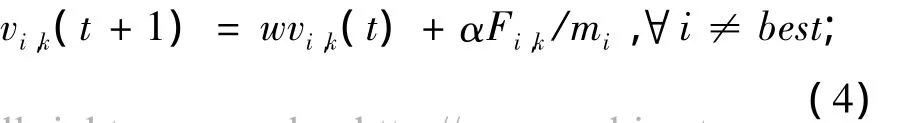
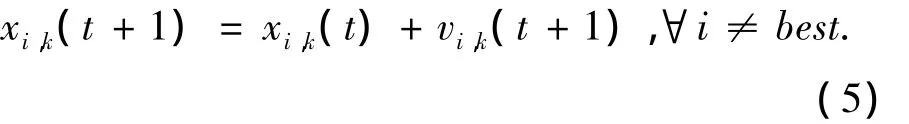
其中w为惯性权重,α~N(0,1)的随机数.任意个体i的运动速度满足Vi=[-Vmax,Vmax],任意个体i的运动空间满足Xi=[Xmin,Xmax].
由式(4)~(5)可以看出,对全局最优个体的速度和位置不进行更新,而直接被保留进入下一次的迭代.
目前,关于APO算法的应用较少,但由于其具有较好的全局搜索能力,不易陷入局部最优,且具有稳定和快速收敛的特点以及较好的鲁棒性优点,将在组合优化问题中有很好的应用前景.
2 结合APO算法的波段选择
结合APO算法的上述优点,本文将该算法应用于高光谱图像的波段选择,其主要包括3个部分:种群初始化,计算个体所受合力以及个体运动更新.
2.1 初始化种群
1)运动空间的设置.根据APO算法中种群个体的特点,首先对高光谱图像按照波段间的相关系数矩阵进行子空间划分[13],设子空间的个数为s,其对应APO算法中个体的维数l,即在每个子空间内选择一个波段(l=s).当然,根据实际目标探测和分类的需要以及计算机快速处理的能力,可以在子空间j(j=1,2,…,s)中同时选择多个波段作为个体在此子空间中的维数lj,个体在所有子空间中维数之和即为个体的总维数,即其中在每个子空间中该选择几个波段,可根据子空间中波段的数目,按一定的比例取值.每个个体代表一个高光谱图像的波段组合,即组合优化问题的一个可行解.这样也使得选择的波段组合相关性小,降低了信息的冗余度.
2)初始化.设置算法中的控制参数以及产生初始种群、初始速度.
控制参数:种群规模为n,每个个体的维数为l,终止迭代次数tmax,引力常量G,惯性权重w=wmax-(wmax-wmin)/tmax×t,初始状态下,个体所受其他个体的虚拟作用力和合力均为零.
初始种群:在确定每个子空间波段序号上、下界的情况下,依次在每个子空间的波段区间范围内,即运动的空间内,随机产生一个n×lj矩阵,且保证矩阵同一行中的元素各不相同(即同一波段组合中选择不同的波段),最后将产生的s个矩阵以列优先的顺序合并为一个n×l矩阵,矩阵中每个元素代表被选中的波段序号,每一行代表一个波段组合,即拟态物理学优化算法中的一个个体,这样产生了n个初始种群个体,本文算法中省去了编、解码的复杂过程,更方便于波段的选择,提高了搜索效率.
初始速度:首先,根据每个子空间中的波段数目,确定个体速度分量在各个子空间中的最大值,则任意个体在第j个子空间中的最大速度计算公式下:
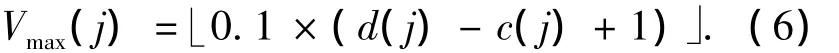
其中c(j)和d(j)表示第j个子空间波段序号的下界和上界.然后,根据个体在该子空间的维数lj,且在最大速度的约束范围Vj=[-Vmax(j),Vmax(j)]内,随机产生速度分量子块vn×lj,以此类推,产生s个速度分量子块.最后,将s个速度分量子块依次按列优先的顺序组成初始速度矩阵Vn×l.其中,初始速度矩阵的每一行依次代表各个个体在每一维上的初始速度.
3)适应度函数.为了使选择的波段组合性能更优,本文采用类间可分性和波段组合的信息量两个性能指标的权重组合作为适应度函数.由于Jeffries-Matusita距离[14]同时兼顾一次统计变量和二次统计变量,在测度高光谱多维空间中两类统计距离时,该距离是最佳测度.因此,本文采用Jeffries-Matusita距离作为适应度函数中的类间可分性函数,其计算如公式为
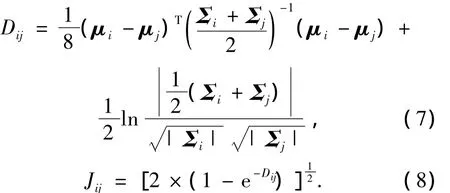
其中:μi、μj分别为第i类和第j类在波段组合上的度量均值矢量;Σi、Σj分别为第i类和第j类在波段组合上的协方差矩阵;T为转置符.
适应度函数中的信息量函数采用最佳索引因子(BOIF)[15],其计算公式下:
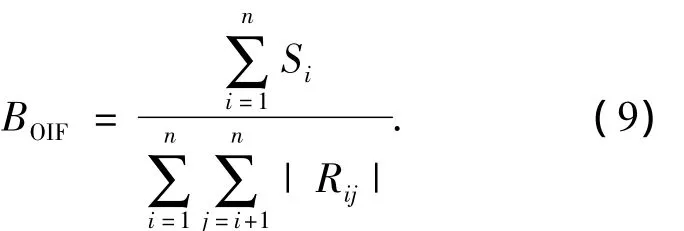
其中:Si为波段i的标准差,且
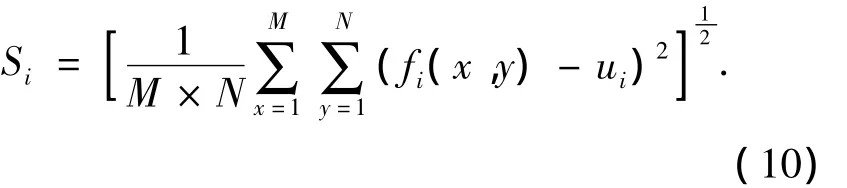
式中:M为图像的行像素个数;N为图像的列像素个数;fi是第i波段;ui是第i波段的像素平均值.Rij为波段i和波段j的相关系数,且
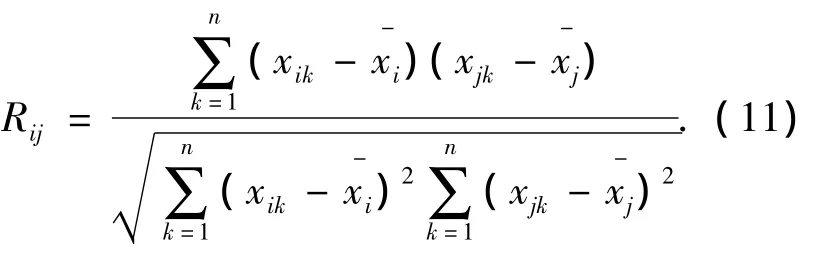
本文采用类间可分性和波段组合的信息量两个性能指标的权重组合作为适应度函数,其计算如式(12),并依据该公式计算初始种群个体的适应度值.
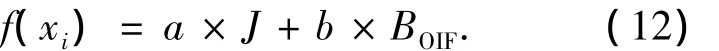
其中a和b为权重系数.
2.2 计算个体所受合力
1)个体质量.在本文的算法中,个体质量与个体的适应度值成正比例关系,即个体适应度值越大,个体的质量就越大;反之亦然.
2)个体所受其他个体的虚拟作用力.个体所受其他个体的虚拟作用力与个体的质量和个体间的距离相关,依据式(2)计算各个个体受其他个体虚拟作用力,适应度值较优的个体对适应度值较差的个体有引力作用,适应度值较差的个体对适应度值较优的个体有斥力作用,且最优个体不受其他个体的作用力,即最优个体不受其他个体引、斥力的作用.依据式(3)计算各个个体受其他个体虚拟作用力合力,这样使得次优的个体逐渐向最优的个体靠拢,最终收敛于最优解.
2.3 个体运动更新
每个个体在其所受合力的作用下进行速度和位置的更新,在算法中引入一个服从正态分布的随机变量α,即α ~ N(0,1),使得个体将以不为零的概率访问高光谱图像子空间中的各个波段,大大提高了算法解的多样性.除了最优个体外,在第t+1次迭代中,其他任意个体按式(4)和式(5)更新每一维的速度和位置,并且保证速度和位置在约束范围之内,对超出约束范围的速度和位置做如式(13)和式(14)的处理.
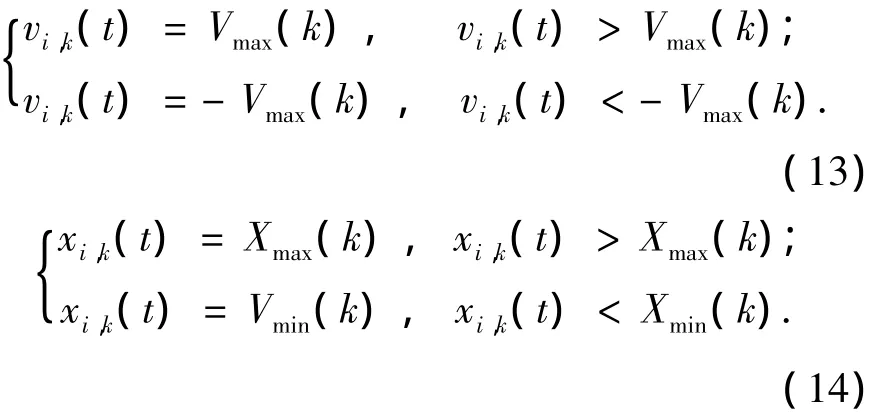
2.4 结合APO算法的高光谱图像波段选择流程
第一步:初始化种群.首先对所处理的高光谱数据进行子空间划分,然后按照2.1节讲述的方法产生初始波段组合种群和初始速度,计算各个个体的适应度值,找到初始种群最优适应度值和最差适应度值,记进化代数t=0.
第二步:计算各个个体所受合力.
1)计算个体的质量:首先根据式(7)~(12)计算个体的适应度值,即波段的组合的适应度值,然后根据式(1)计算个体的质量;
2)根据式(2)计算各个个体所受其他个体的虚拟作用力;
3)根据式(3)计算个体所受其他个体作用力合力.
第三步:计算各个个体的运动.
根据式(4)和式(5)更新个体的运动速度和位置,且使更新后的个体运动满足式(13)和式(14)所示的速度和位置的约束条件.
第四步:计算个体的适应度值.
计算更新后的个体适应度值,更新最优适应度值和最差适应度值.
第五步:判断算法结束条件.
本文设计的算法结束条件是最大迭代次数,若满足,则停止循环,并输出最优解;若不满足,进行迭代次数t=t+1,返回第二步继续执行,直至达到最大迭代次数为止.
本文算法的流程如图1所示.
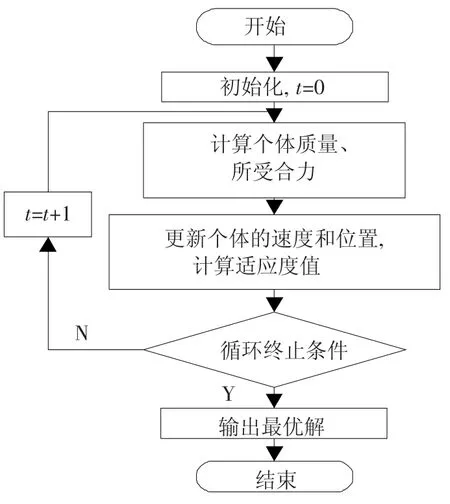
图1 波段选择流程
3 波段选择的结果与评估
本文的硬件环境是:CPU为 Intel Core i3,2.40 GHz,内存 2 GB的 PC机;软件环境是:Window XP操作系统,利用Matlab 2008a对波段选择算法进行仿真实验;实验数据:本实验所采用的高光谱AVIRIS数据为1992年6月美国西北部印第安纳州农林混合试验场的高光谱图像,其光谱范围为0.41~2.45 μm,空间分辨率为25 m,光谱分辨率为 10 nm,图像的大小为 144×144 pixel,在原始220个波段的图像中,去除水汽吸收和低信噪比的波段,参与处理的图像波段数为200.实验中选择的地物类别以及训练样本数和测试样本数如表1所示.
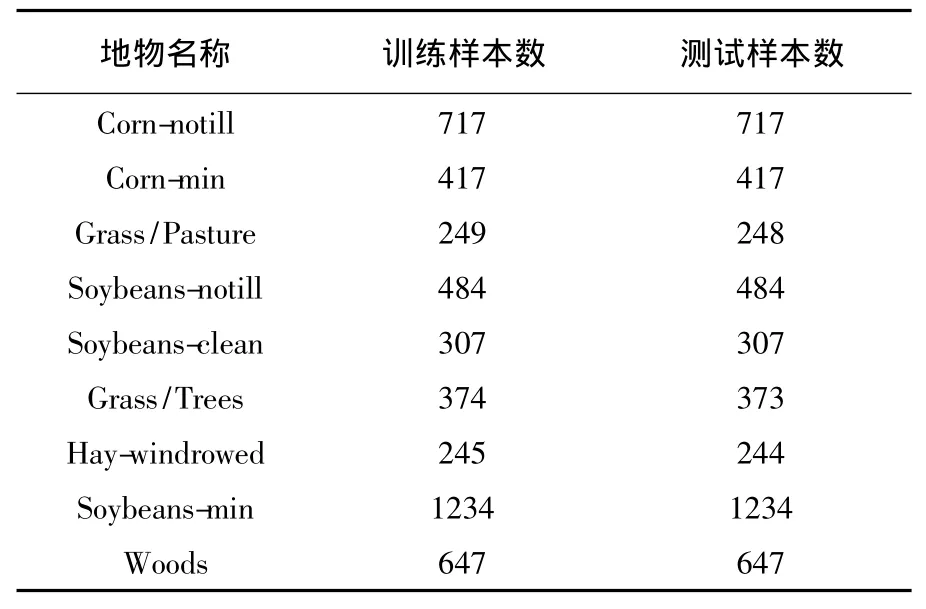
表1 实验数据
本文算法中参数设置[12,16]为:wmin=0.4,wmax=0.9,tmax=200,n=30,l=s=5,G=1,a=40,b=1e-5.为证明本文算法是一种有效的波段选择方法,用基于蚁群、遗传和粒子群算法的波段选择与本文提出算法从精解效率和搜索效率两个方面进行对比.精解效率是从每种算法输出最优波段组合的相关性、信息量和总体分类精度3个方面进行评判.相关性越小越好,信息量越大越好,分类精度越高越好.本文用最大似然分类法对输出的最优波段组合图像进行分类,求出其总体分类精度,其计算公式如下:
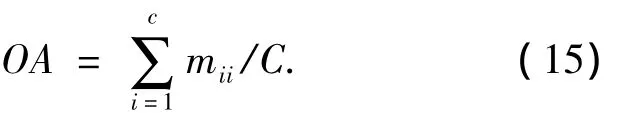
其中:c为类别数;C为c类测试样本总数;mii为第i类正确分类个数.
相关性采用波段组合波段间的平均相关性,其计算公式为
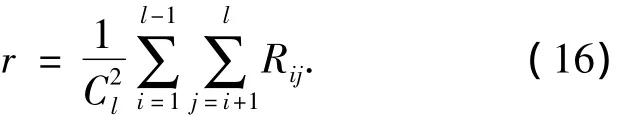
信息量采用最佳索引因子(OIF).实验中,各对比算法均结合了子空间划分进行波段子集的选择,且对比算法中参数的设置参考文献[17-19].实验对比结果如表2~4,其中表2为表1中前3种地物类别情况下得到的结果,表3为表1中前5种地物类别情况下得到的结果,表4为表1中9种地物类别情况下得到的结果.

表2 3种地物类别下的不同算法比较

表3 5种地物类别下的不同算法比较

表4 9种地物类别下的不同算法比较
由表2~表4可以看出:本文提出算法搜索到较优解的时间效率都优于其他算法,尤其本文算法的收敛速度远远快于蚁群算法,而且随着地物类别数的增加,本文算法的搜索效率的优越性更加明显;本文算法选择的波段子集在精解效率(即平均相关性、信息量和总体分类精度)方面也优于蚁群算法.本文算法和遗传算法相比,尽管遗传算法执行了更多的迭代次数,但是其收敛到最优解性能远次于本文算法搜索到最优解的性能,这是由遗传算法有较强的全局寻优能力、而局部寻优能力比较差的特点所造成的.本文算法与粒子群算法相比,除了在信息量方面低于粒子群算法,在其他方面,本文算法都优于粒子群算法.再者,本文算法收敛到最优解的性能较优,另一主要原因是本文算法中将类间可分性和波段组合的信息量两个性能指标以一定的权重组合方式作为适应度函数进行寻优.
为了更清晰、直观地反映本文算法的有效性,将本文算法最优解与其他算法的最优解分类结果比较如图2~图4所示.
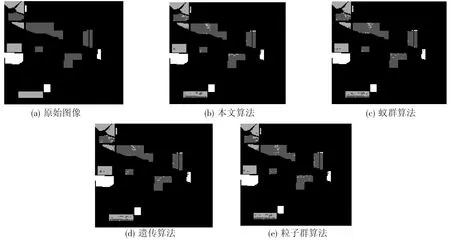
图23 种地物类别情况下不同算法最优解的分类
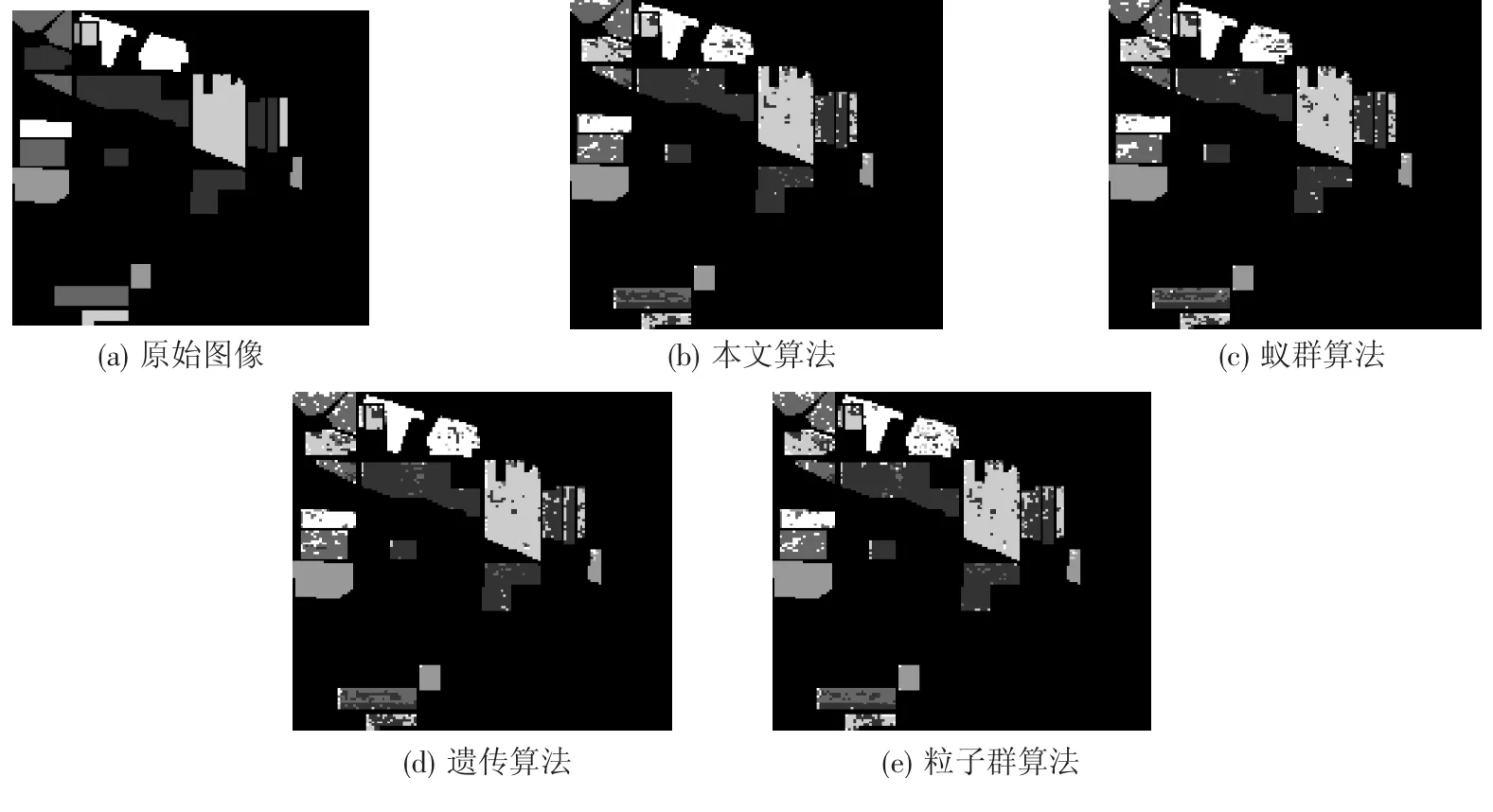
图35 种地物类别情况下不同算法最优解的分类
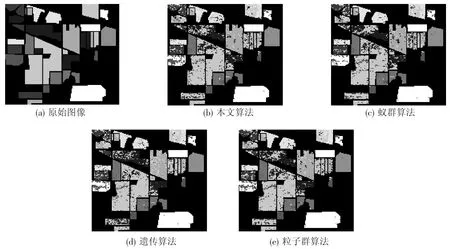
图49 种地物类别情况下不同算法最优解的分类
4 结论
利用高光谱图像波段选择来去除冗余信息是高光谱图像分类、识别的关键步骤,近些年来,提出了许多方法进行高光谱图像波段选择,但同时兼顾搜索效率和精解效率仍是目前高光谱图像波段选择中常常遇到的困难.在本文的算法中,采用了类间可分性和波段组合的信息量两个主要性能指标的权重组合作为了适应度函数,此外,在波段选择之前对高光谱图像进行了子空间划分,使得最优解中的波段间相关性较小,冗余度低.本文算法与基于蚁群、遗传和粒子群算法的波段选择方法相比,本文方法是一种搜索效率和精解效率都比较好的波段选择方法,实验也证明了该算法的有效性.
值得注意的是,本文提出算法中引力参量G需要进行设置,而且其不同的取值对较优波段组合的选择有一定的影响,但又很难确定其最佳值.虽然本文根据具体实验数据进行反复测试和观察,进而取得一个较优值,但一种更好的引力参数确定方法有待进一步研究.
[1]丁胜,袁修孝,陈黎.粒子群优化算法用于高光谱遥感影像分类的自动波段选择[J].测绘学报,2010,39(3):257.
[2]吴昊,李士进,林林,等.多策略结合的高光谱图像波段选择新方法[J].计算机科学与探索,2010,4(5):464-472.
[3]王力军,欧吉顺,周楚新.一种改进的基于禁忌搜索的特征选择算法[J].中国制造业信息化,2011,40(5):63.
[4]赵冬,赵光恒.基于改进遗传算法的高光谱图像波段选择[J].中国科学院研究生院学报,2009,26(6):795-802.
[5]周爽.蚁群算法在高光谱图像降维和分类中的应用研究[D].哈尔滨:哈尔滨工业大学,2010:42-49.
[6]黄睿.高光谱遥感数据特征约简技术的研究[D].西安:西北工业大学,2005:79-89.
[7]刘颖,谷延锋,张晔,等.一种高光谱图像波段选择的快速混合搜索算法[J].光学技术,2007,33(2):258-261,265.
[8]倪霖,郑洪英.基于免疫粒子群算法的特征选择[J].计算机应用,2007,27(12):2922-2924.
[9]王艳,曾建潮.解决多目标优化问题的拟态物理学优化算法[J].计算机工程,2010,36(20):188.
[10]SPEARS W M,SPEARS D F,HEIL R,et al.An overview of physicomimetics.Lecture Notes in Computer Science-State of the Art Series,2005,3324:84-97.
[11]王艳.多目标拟态物理学优化算法及其应用研究[D].兰州:兰州理工大学,2011:23-30.
[12]MO Simin,ZENG Jianchao.Performance analysis of the artificial physics optimization algorithm with simple neighborhood topologies[C]//Computational Intelligence and Security.Beijing:[s.n.],2009:155-160.
[13]JIAX,RICHARDSJA.Segmented principal components transformation for efficient hyperspectral remote sensing image display and classification[J].IEEE Trans.Geosci.and Remote Sensing,1999,37:538-542.
[14]WACKER A G.The minimum distance approach to classification[D].West Lafayette:Purdue University,1971.
[15]CHAVEZ P S,BERLIN G L,SOWERS L B.Statistical method for selecting landsat MSS ratios[J].Journal of Applied Photographic Engineering,1982,8:23-30.
[16]XIELiping,TANYing,ZENGJianchao.The convergence analysis and parameter selection of artificial physics optimization algorithm[C]//Modelling,Identification and Control.Okayama:[s.n.],2010:562-567.
[17]马江涛.基于遗传与蚁群的混合算法路径优化研究[D].湖北:湖北工业大学,2011:16-17.
[18]武交峰.应用遗传算法提高蚁群算法性能的研究[D].太原:太原理工大学,2004:37-53.
[19]毕晓君.信息智能处理技术[M].北京:电子工业出版社,2010:197-199,257-265.
