带时延估计的时间差分PLS软测量建模方法

阮宏镁，田学民，王平

（中国石油大学（华东）信息与控制工程学院，山东 青岛266580）

实际工业过程中存在一些与产品质量密切相关，需要加以严格监控的重要过程参数。由于技术或经济的原因这些参数尚难以用传感器直接测量，目前主要通过化验室离线采样化验分析得到，导致测量滞后大，从而无法实时监控产品的质量，对此，软测量技术［1］是解决该问题的有效途径。

基于数据驱动［2］的软测量建模方法，是一种基于过程历史数据的经验方法，不需要了解过程内部复杂的机理，因而得到了广泛的应用。其中主成分分析 PCA （Principle Component Analysis）［3］、偏最小二乘 PLS （Partial Least Squares）［4］等建模方法，算法结构简单，解决了共线性问题，同时降低了输入空间的维数，然而这些方法只能有效地处理数据间的线性关系，不能反映出变量间的非线性关系。因此，人们提出了核偏最小二乘KPLS（Kernel PLS）［5－6］、人工神经网络 ANN （Artificial Neural Networks）［7］、支持向量基 SVM （Support Vector Machines）［8－9］等非线性建模方法。这些方法在一定程度上克服了线性建模方法的不足，但另一方面又失去了线性建模方法的良好特性，存在模型结构和模型参数难以确定，计算求解繁琐等问题。由于模型对非线性的逼近精度很大程度上取决于模型的复杂程度，模型对过程非线性的逼近能力和模型复杂程度间存在着矛盾。

实际工业过程软测量模型的建立不仅受到过程非线性的影响，过程时延也给软测量模型的建立带来很大困难。时间滞后在系统中普遍存在，如储蓄单元引起的容积时延、信号传输带来的纯时延等，使软测量模型的精度受到很大影响，因而要建立高精度的软测量模型，准确估计过程时延是十分必要的。过程时延通常是在对工艺机理进行深入分析的情况下，依据先验知识来确定的，然而对于较复杂的生产过程来说，该方法存在着较大的随机性。另外，相关分析法［10］根据输入输出变量间的相关程度可较好地估计时延，然而该方法独立地分析各输入变量与输出变量的关系，易陷入局部最优，且相关分析法只能分析变量间的线性相关程度，因而不适用于非线性系统的时延估计。

针对以上两个典型问题，笔者提出一种带时延估计的时间差分PLS软测量建模方法。时间差分PLS模型用当前时刻输入输出变量与之前某一时刻输入输出变量的差值作为新的建模样本，然后基于PLS建立软测量模型，不仅充分保留了线性PLS模型的良好特性，并且提高了模型对过程非线性逼近的精度。另外，将时延估计问题转化为多维非线性优化问题，由具有全局搜索能力的差分进化算法求解，从而得到全局最优解。最后，采用工业常压塔的实际生产数据建立软测量模型对本文方法进行验证。

1 带时延估计的时间差分PLS建模方法

1.1 时间差分PLS模型

PLS［11］可用外部关系和内部关系来描述，外部关系分别对输入变量矩阵X与输出变量矩阵Y进行分解，内部关系则是描述输入变量矩阵X与输出变量矩阵Y之间的关系。对于输入变量X，输出变量Y，采用PLS方法进行分解，如下式所示：

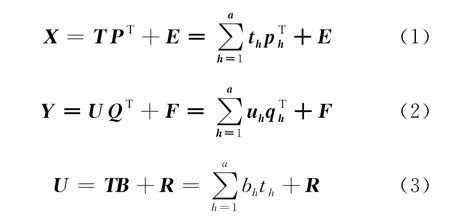
式中：T——X中提取的主元矩阵；U——Y中提取的主元矩阵；P——X的负荷矩阵；Q——Y 的负荷矩阵；B——系数矩阵；E——X 的残差矩阵；F——Y的残差矩阵；R——U的残差矩阵。

PLS模型结构简单、物理意义明确，可有效地克服共线性问题，且使模型包含最少的独立变量数。但是PLS本质上是一种线性回归方法，处理非线性过程的建模问题时模型精度不够，因而笔者引入时间差分模型。

传统的软测量模型直接寻找辅助变量X（t）与主导变量y（t）之间的函数关系。时间差分模型［12－13］则首先计算差分量 ΔX（t），Δy（t），即计算辅助变量X（t），主导变量y（t）当前时刻的值X（t），y（t）与i时刻之前的值X（t－i），y（t－i）的差值。

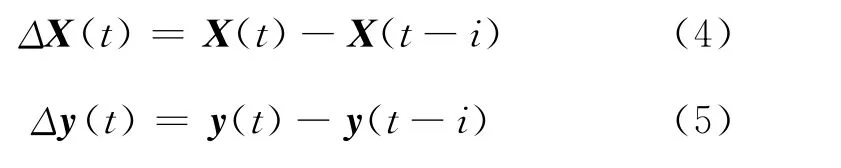
然后再建立ΔX（t），Δy（t）之间的模型，预测时先计算新数据X（t′）的差分量，再代入已建立的模型中得到模型的预测值y（t′）的差分量 Δy（t′），X（t′）的差分量计算如下：

模型的预测值y（t′）计算如下，其中y（t′－i）是已知的。

假设非线性过程模型如下：

在任意点x0＝ ［x10，x20，…，xm0］处进行泰勒展开，略去高次项得：

进一步可表达为

由式（10）可知时间差分模型建立Δx，Δy间的线性回归模型，即非线性模型（8）的梯度模型，这在一定程度上提高了模型对非线性过程的逼近能力，从而提高了建模精度。

1.2 基于DE的时延估计

非线性时延过程可表示为如下形式：

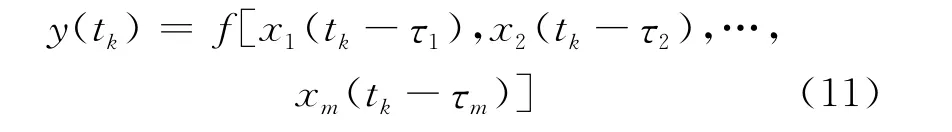
式中：y（tk）——tk时刻过程的输出值；xi——过程的输入值，i＝1，…，m；τi——第i个输入变量与输出变量之间的时延值，i＝1，…，m。

对该过程建立软测量模型，假设建立基于PLS的软测量模型，模型如下：

式中：yPLS（tk）——PLS模型输出值；xi——PLS模型输入值，i＝1，…，m；τ′i——第i个输入变量与输出变量之间的时延估计值，i＝1，…，m。

从而非线性过程的时延估计问题可表示为如下的非线性优化问题：

其中约束条件根据过程先验知识确定，各输入变量的时延值τi取值范围 在 ［τinf，τsup］，τinf，τsup为时延值的上下限，且τi是输入变量采样时间TX的整数倍，过程输出变量的采样时刻tk是输出变量采样时间TY的整数倍。

显然，上述优化问题是一个复杂的多维非线性约束优化问题，因而考虑用差分进化算法DE（Differential Evolution）求解该优化问题。在上述约束条件限制的范围内，搜索最优决策变量τi，使目标函数J，即实际输出值与软测量模型预测输出值间的误差平方和SSE最小。

DE算法是一种基于群体智能理论的优化算法，采用实数编码，通过种群内个体间的合作和竞争产生的群智能指导优化搜索，具有容易理解、易于实现、搜索能力强等优点［14］。

对于式（13）所示的约束优化问题，DE寻优的实现步骤如下：

2）假设当前种群为第k代，对于该种群每一个体Xik（1≤i≤N ），由变异、交叉、选择，产生下一代个体 Xik＋1（1≤i≤N ）。在进行变异操作后，产生的新一代种群中一些个体的某些维的值会不满足约束条件，将这些不满足条件的值由随机初始化产生的新值取代。

3）若算法满足终止条件J≤e或k≥NG则算法结束，终止进化，否则返回步骤2）。e为模型允许的最大误差，NG为最大进化代数。

1.3 算法实现步骤

带时延估计的时间差分PLS算法步骤如图1所示。

图1 算法实现步骤

1）初始化DE参数，最大进化代数NG，模型允许的最大误差e。

2）由DE算法进行全局搜索，寻找最优的时延参数值τ，根据得到的时延值选取对应的输入输出数据X（t－τ），y（t）。

3）根据式（4），（5）计算时间差分量 Δy（t），ΔX（t－τ）。

4）建立ΔX（t－τ），Δy（t）之间的PLS模型，求得模型估计值ypis（tk）。

2 仿真研究

常压塔是石油化工生产过程中的重要装置，其侧线产品的质量指标是备受关注的重要过程参数，往往通过化验分析得到，一般是每隔8h或4h采样一次，无法保证产品质量和生产操作的连续稳定。因此，通过建立侧线产品质量指标的软测量模型实现产品质量的实时监测与控制。

本文建立常二线干点的软测量模型，根据常压塔装置的机理、工艺流程和专家经验，结合相关分析法选择塔顶压力、塔顶温度、侧线抽出量和抽出温度等14个密切相关的过程变量作为常二线干点软测量模型的辅助变量。生产数据从某石化公司获得，经过数据处理之后得到158组数据，辅助变量由DCS获取，每30s采样一次，主导变量由实验室分析得到，每天8点、12点各采样一次。

取其中前120组作为训练样本集，建立软测量模型，剩余38组作为测试样本集，评价模型泛化能力。需要优化的变量为各辅助变量相对主导变量的时延τ，搜索范围都设为［0，120min］且取采样时间TX＝30s的整数倍，显然问题维数n，即辅助变量个数为14个，设置最大进化代数NG＝200，种群规模N＝140，变异概率F＝0.1，交叉概率CR＝0.3。

为了验证文中所提方法的有效性，分别由相关分析估计时延建立时间差分PLS模型，由DE估计时延建立PLS模型，与本文由DE估计时延建立时间差分模型做比较，选取的标准是使测试数据的均方误差MSE达到最小。表1给出了3种软测量模型的结果，比较表1第1行和第2行可以看出，均建立时间差分模型，DE估计时延建立模型的预测误差明显小于由相关分析法估计时延建立模型的预测误差。比较表1第1行和第3行可以看出，均采用DE估计时延，时间差分模型的预测误差明显小于PLS模型的预测误差，由以上分析可见带时延估计的时间差分PLS模型可显著提高模型精度和泛化能力。

表1 3种软测量模型结果比较

为了更直观地比较3种软测量模型的预测效果，图2～图4给出3种软测量模型的测试结果。由DE算法估计时延建立PLS模型得到结果如图2所示；由相关分析估计时延建立时间差分PLS模型得到结果如图3所示；本文提到的由DE算法估计时延建立时间差分PLS模型得到结果如图4所示，分别比较图2和图4，图3和图4，可以看出笔者所提方法建立软测量模型所得预测曲线可以更好地逼近工业实际曲线。

图2 DE估计时延的PLS建模结果

图3 相关分析估计时延的时间差分建模结果

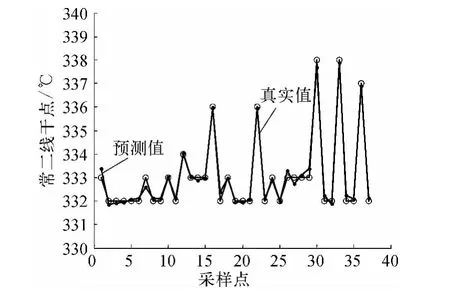
图4 DE估计时延的时间差分建模结果

3 结束语

笔者结合时间差分PLS建模方法与基于DE的时延估计方法分别解决实际工业过程中的非线性和时延估计等问题。时间差分PLS模型建立非线性过程的梯度模型，増强了PLS逼近非线性过程的能力，同时保持了PLS建模方法的优点。采用DE算法估计时延，进一步提高了软测量模型精度。对常压塔二线干点数据进行仿真应用取得了很好的效果，模型的精度和泛化能力得到提高，表明本文方法的有效性。

［1］俞金寿，刘爱伦，张克进.软测量技术及其在石油化工中的应用［M］.北京：化学工业出版社，2000.

［2］KADLEC P，GABRYS B，STRANDT S.Data－driven Soft Sensors in the Process Industry ［J］.Computers and Chemical Engineering，2009，33（04）：795－814.

［3］LIN B，RECKE B，KNUDSEN J K H，et al.A Systematic Approach for Soft Sensor Development［J］.Computers and Chemical Engineering，2007，31（05）：419－425.

［4］KANO M，MIYAZAKI K，HASEBE S，et al.Inferential Control System of Distillation Compositions Using Dynamic Partial Least Squares Regression ［J］.Journal of Process Control，2000，10（02）：157－166.

［5］ROSIPAL R.Kernel Partial Least Squares for Nonlinear Regression and Discrimination［J］.Neural Network World，2003，13（03）：291－300.

［6］ROSIPAL R，TREJO L J.Kernel Partial Least Squares Regression in Reproducing Kernel Hilbert Space ［J］.Journal of Machine Learning Research，2002（02）：97－123.

［7］ROGINA A，ŠIŠKO I，MOHLER I，et al.Soft Sensor for Continuous Product Quality Estimation（in Crude Distillation Unit）［J］.Chemical Engineering Research and Design，2011，89（10）：2070－2077.

［8］YAN Weiwu，SHAO Huihe，WANG Xiaofan.Soft Sensing Modeling Based on Support Vector Machine and Bayesian Model Selection［J］.Computers and Chemical Engineering，2004，28（08）：1489－1498.

［9］林碧华，顾幸生.基于差分进化算法－最小二乘支持向量机的软测量建模［J］.化工学报，2008，59（07）：1681－1685.

［10］傅永峰.软测量建模方法研究及其工业应用［D］.杭州：浙江大学，2007.

［11］李浩，杨敏，石向荣，等.基于主曲线的软测量方法及其在精馏塔上的应用［J］.化工学报，2012，63（08）：2492－2499.

［12］KANEKO H，FUNATSU K.Maintenance－free Soft Sensor Models with Time Difference of Process Variables ［J］.Chemometrics and Intelligent Laboratory Systems，2011，107（02）：312－317.

［13］KANEKO H，FUNATSU K.A Soft Sensor Method Based on Values Predicted from Multiple Intervals of Time Difference for Improvement and Estimation of Prediction Accuracy ［J］.Chemometrics and Intelligent Laboratory Systems，2011，109（02）：197－206.

［14］王钧炎，黄德先.基于混合差分进化算法的软测量时延参数估计［J］.化工学报，2008，59（08）：2058－2064.