基于Dahlin算法的变风量空调自校正PID控制
2013-08-31孟祥懿付东翔王亚刚
孟祥懿,付东翔,王亚刚
(上海理工大学 光电信息与计算机工程学院,上海200093)
变风量空调系统是为满足节能的要求而出现的,由于外界气候和空调区域内人员的活动变化很大,对系统形成了很大的干扰,难以实现稳定控制,系统表现出含有纯滞后环节,容易引起系统超调,甚至振荡。但这些过程对系统的稳定性和有较小超调的要求恰恰是主要的参数要求。PID控制根据不同被控对象适当整定PID 3个参数,可以获得比较满意的控制效果,但这些整定无法解决稳定性和精确性的矛盾。Clarke[1]等人提出了广义预测控制算法,该算法基于参数模型引入了不相等的预测和控制水平,能使具有大滞后的系统具有更好的控制性能。特点是预先估计出过程在基本扰动下的动态特性,然后由预估器进行补偿,力图使被延迟了的被调量超前反映到控制量,使控制提前动作,从而明显地减小超调量并加速调节过程。由于系统中含有纯滞后环节,使控制器设计变得复杂,对控制系统稳定性极其不利[2-4]。
笔者以空调系统为控制对象,基于Dahlin算法设计了自校正PID控制器,利用带遗忘因子的最小二乘法,实时进行控制对象的传递函数的参数估计,建立了系统PID参数之间的关系式,并通过改进的整定方法,实现变风量空调系统的末端控制[5]。算法仿真运算及实验表明,与传统PID及模型预测控制方法相比,该方法控制精度高于传统PID,同时计算复杂度低于通常模型预测控制自校正算法[6]。
1 自校正控制原理
自校正控制是在某种确定的调解器结构条件下,使控制系统达到最佳的控制性能,具有以下特点:利用辨识方法,确定被控对象的数学模型,根据辨识结果,决定自适应控制对策,调整调节器的参数,使控制回路性能达到最优。如果系统的模型和噪声模型未知或者模型的参数是时变的,那么就需要把辨识算法和控制算法有机结合起来,即构成参数自适应控制算法,如图1所示。

图1 自校正PID控制系统结构
需要进行的工作:1)选择调节器的结构,本文采用PID进行调节;2)选择描述被控对象的模型,模型参数记作θ;3)基于被控对象的输入输出数据,在线辨识模型的参数θ;4)设计调节器的参数β,通常是被控对象模型参数θ ^的函数,记作β ^=β(θ ^)。
2 空调系统模型与辨识
2.1 被控对象模型
2.1.1 末端风阀
在空调系统中,风阀是系统必不可少的组成部分,变风量空调系统,通过调节末端风阀开度来调节进入房间的风量,末端风阀采用的是电动调节阀,其动态特性取决于电动执行机构开关的时间,末端风阀控制信号与风阀开度的关系为

式中:C——归一化的风阀行程(风阀相对开度);Ci——控制信号,-0.5~+0.5(-为关闭方向,+为开正方向)。末端风阀在最大控制信号+0.5作用下,从0至1需要60s,故τ0.5=30s,考虑到变风量末端的额定风量为0.8m/s,再乘以一个放大倍数K,得到末端风阀的传递函数为

2.1.2 空调房间模型
建立实验平台空调系统数学模型过程中,为利于解决问题做一些必要的简化,并做一假设:室内各处温度趋于平均,根据热力学第一定律,由空调房间储能的变化率=单位时间内进入房间的能量-单位时间内房间排出的能量,得到数学模型:

式中:L——送风量,m3/h;Qx——空调房间热负荷,W;ρ——空气密度,kg/m3;c——空气的比热容,kJ/(kg·℃);tn,ts——室内空气温度和送风温度,℃。
取某一时刻,Qx=Q0,L=L0,tn=tn0,ts=ts0,由于房间是恒温室,因此Q0-L0ρc(tn0-ts0)=0。对式(3)在工作点按泰勒级数展开,进行适当处理得,CpdΔtn/dt-L0ρcΔtn=ΔQ-ρc(tn0-ts0)×ΔL+ρc L0Δts进行拉普拉斯变换,得:

从以上分析可以看出空调房间的模型可以视为一阶惯性环节,但由于空调系统通常都有一定的延迟,因此要考虑滞后时间τ2,式(4)调整为G2(s)=K2ex p(-τ2)/(T2s+1)。
为了使用上位机对空调系统进行在线辨识,需要对空调系统数学模型的传递函数表达式进行离散化,得:G(z-1)=Z[G1(s)G2(s)(1-eTs)/s],可以化为:

式中:e(k)——零均值白噪声干扰;d——输出延迟。
2.2 模型辨识算法
本文仿真的实时参数估计采用遗忘因子递推最小二乘法[7],更能适应参数突变但不频繁,参数缓慢变化的情况,被控对象为单输入单输出系统。
由式(5)CAR模型得到:

参数向量为

数据信息向量为
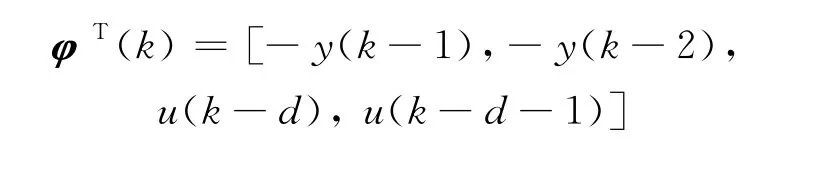
2.3 增量式PID控制算法
本文采用增量式 PID控制算法,Δu(k)=kP(e(k)-e(k-1))+kIe(k)+kD(e(k)-2e(k-1)+e(k-2)),kP,kI,kD为PID调节参数,也可表示为Δu(k)=g0e(k)+g1e(k-1)+g2e(k-2),其中gi(i=0,1,2)为可调参数,得PID控制器离散时间传递函数为

3 改进的整定方法
Dahlin提出的将系统校正成一阶惯性纯滞后系统的设计方法,解决了具有纯滞后特性的被控对象对稳定性、超调量的要求较高这一问题[8]。Dahlin控制器具有很多优点,但在实际工程中的使用并不是很多,主要原因是Dahlin控制器会产生振铃现象,消除该现象的传统方法有修改控制器或修改闭环期望传递函数的设计方法[9]。笔者给出一种更好的能够避免产生振铃现象的设计方法,即简化了的Dahlin自校正PID控制器,Dahlin控制系统如图2所示。

图2 Dahlin控制系统示意
从图2可以看出,D(z-1)是数字调节器,HG(s)是被控过程的脉冲传递函数,系统的闭环传递函数为

得Dahlin控制器为

根据Dahlin算法,期望的闭环响应可以是一阶惯性加纯滞后的形式:

Z变换得:

式中:λ——闭环系统的等效时间常数;τ——纯滞后时间,τ=NT,N 为正整数;T——采样周期;a=e-T/λ。
由式(5)可知:

把式(8),(9)带入式(7)得:

为了使D(z-1)能用来调节PID参数、防止振铃现象出现,并与式(6)形式符合,做以下改进:式(10)中,如果b0+b1z-1=0的根位于单位圆外或者位于左半单位圆内靠近-1,则控制器的输出将发散或者发生振铃现象,为避免该现象发生,在不影响控制器增益的情况下,作如下简化,令z-1=1,得b0+b1z-1=b0+b1,因此算法的增益没有受影响,不影响稳定性,得:

为了进一步与式(6)控制器离散时间传递函数相匹配,作如下化简:

同理,在不改变算法增益的前提下,令z-1=1,得到了符合PID调节的对应参数方程:

最后,参数调节公式可以令式(6)和式(11)相等,得PID参数的系数公式为

4 仿真实验
针对广义预测自校正算法和改进Dahlin自校正PID算法,在Matlab中分别进行了仿真实验,对两种控制器的控制效果对比,广义预测自校正算法和系统辨识参数设计如下:Nu=1,N1=1,N2=15,遗忘因子λ=1,输出柔化系数α=0.7;对于改进Dahlin自校正PID算法,参数设计为遗忘因子λ=1,q=0.9。
两种算法的仿真曲线如图3,4中,yr(t),y(t),u(t)分别为系统的参考输入、实际输出、控制量。在系统的初始阶段,需要对参数进行估计,故控制效果不是很理想,辨识出系统参数后,两种控制算法分别呈现较好的控制效果。系统的输出基本满足参考输出的变化,同时控制量也能随着系统的变化做出相应的调整。当系统运行到200s时,改变广义预测自校正算法和改进的Dahlin自校正算法的系统模型参数,使系统处于第二个运行状态。在模型改变的瞬间,出现了振荡,但经过一段时间的调节,系统输出很快就趋向于设定值,这样的效果是由于系统通过在线辨识控制对象的参数来修正控制器参数,控制算法具有较强的跟踪性能和自适应能力。笔者所提出改进的Dahlin控制效果优于广义预测自校正算法,对类似于温度对象的非线性、纯滞后环节的系统具有很好的控制效果。

图3 广义预测自校正算法


图4 Dahlin自校正PID
5 结束语
在变风量空调末端控制中,应用了改进的Dahlin自校正PID算法,该算法具有计算量小,可以在线自动辨识被控对象模型参数、自动整定控制器参数,同时具有常规PID控制器结构简单、鲁棒性好的特点,通过仿真对比,改进的算法在控制效果上,综合性能优于传统的PID算法、广义预测自校正算法。
[1]CLARK D W,MOHTADI C,TUFFS P S.Generalized Predictive Control [J].Automatica,1987,23(02):137-160.
[2]方崇智,萧德云.过程辨识[M].北京:清华大学出版社,1998:201-208.
[3]谢新民,丁锋 .自适应控制系统 [M].北京:清华大学出版社,2002.
[4]ASIROM K J.Adaptive Control[M].Peking:Press of science,2003.
[5]SALSBURY T A.Survey of Control Technologies in the Building Automation Industry [C]//16thIFAC World Congress.Prague:IFAC,2005.
[6]QU G,ZAHEER-UDDIN M.Online H∞Adaptive Tuning of PIControllers for Discharge Air Temperature System[J].Energy Conversion and Management,2010,51(06):1179-1195.
[7]ZAHEER-UDDIN M.Combined Energy Balance and Recursiveleast Squares Method for the Identification of System Parameters [G ]//ASHRAE Transactions.ASHRAE,1990,96(02):239-244.
[8]VLADIMIR B,PETR C,PETR D.Application of Polynomial Methods for Design of Adaptive Decentralize Control [C]//2004IEEE International Symposium on Computer Aided Control Systems Design.Taipei:IEEE,2004.
[9]BOBAL V,BOHM J,FESSL J,et al.Digital Self-turning Controlers Algorithms,Implementation and Applications[M].London:Springer,2005.
