基于混沌时间序列模型的图书借阅流量预测研究

●田 梅 a，b（新乡医学院 a.管理学院； b.卫生信息资源研究中心,河南 新乡 453003）

目前国内对图书借阅流量行为预测的研究，多集中在利用统计学理论和平稳时间序列模型进行建模。姜炳蔚等利用回归分析的方法建立图书流通量与时间的回归方程，并计算出预测范围；[1]吴红艳[2]利用A R I M A时间序列理论和神经网络理论为基础预测图书借阅流量，提出了处理具有周期性时间序列问题的季节性神经网络模型。此外，传统的图书借阅量的预测方法还包括灰色模型预测法、线性回归法等。但这些方法都存在着自身固有的缺陷。由于图书借阅预报本质是一个复杂的非线性动力学过程，其内部运行关系很难确定，呈现非平稳动态随机变化特性，因此，传统的时间序列预测模型、线性回归都难以解决阅读流量行为的非线性问题，无法解决流量增长的某些不稳定变化对模型预测效果的影响。而利用神经网络建模，又容易陷入局部极小值问题，所得到的模型无法提供良好的推广能力。

本文以混沌时间序列理论和支持向量机为基础，提出了处理非线性图书借阅流量问题的混沌时间序列预测模型。该模型根据图书借阅流量行为的非平稳时间序列的数据特点，分别求得时间序列的嵌入维数和时延，从而建立了单步预测模型。利用该模型对新乡医学院图书馆流通部每月的图书借阅流量进行监测预报，结果表明，该模型运行高效，与常规的神经网络模型相比，预测精度有所提高。

1 支持向量机

支持向量机是建立在统计学习理论基础上的一种学习算法，以解决小样本学习问题为目标。与已有的机器学习算法相比，它寻求模型的复杂性和学习能力之间的最佳折衷，以获得有限样本信息下的最优推广能力，避免了过学习现象；它所构建的优化目标函数是一个严格的凸二次型规划，从而保证了全局唯一解。通过引入核函数，将原始空间中线性不可分样本通过非线性函数映射到高维特征空间，实现线性可分。同时，通过将高维特征空间中的内积运算转化为低维原始空间的核函数计算，有效解决了高维数据学习中的“维数灾难”问题，计算量几乎不受样本维数影响，从而实现了良好的高维处理能力。由于支持向量机在解决非线性及高维模式识别问题中表现出特有的优势，因此成为目前的研究热点，在文本自动分类、图像检索、数据融合、信号处理、时间序列预测等领域得到了广泛应用。

以ε-支持向量回归为例。它的核心思路是把超平面控制在ε管道内，由ε值控制管道的宽度并决定支持向量回归的误差要求，同时管道尽可能平坦。根据统计学理论，决策函数的计算转换成如下的最优化问题：[3]

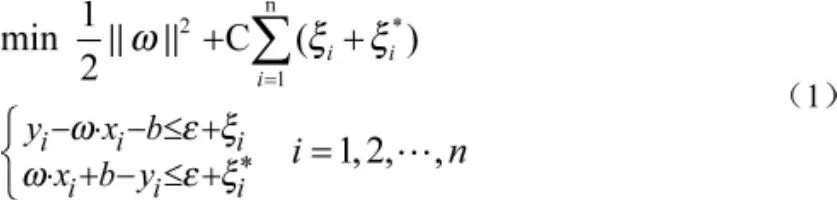
构造Lagrange乘子方程转换到对偶问题：

可以得出决策函数为：

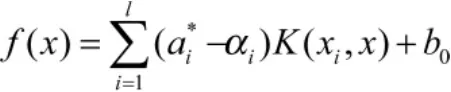
2 混沌时间序列预测模型

混沌时间序列在现实生活中随处可见，比如电力载荷、金融、股票价格、大气、水文数据等。通常计算出某时间序列的最大Lyapunov指数，即可确定其是否具有混沌特性。使用SVM可以对混沌时间序列进行预测，预测的重点在于确定时间序列的嵌入维数和时延，从而构建能够反映原时间序列数据所蕴含动力系统本质的状态空间，从而达到较高精度的预测效果。

理论上，时间序列本身已包含了参与此动力系统的全部变量的有关信息，通过考察采样得到的样本，将它在某些固定时间延迟点上的观测量看成新的坐标，以扩展成一个高维空间，即重构的状态空间。根据重构的混沌时间序列输入向量和输出向量进行学习， 时刻支持向量机的一步预测模型为：[4]

3 应用研究

3.1 数据采集

本文中采用的图书流通量数据，来自于新乡医学院图书馆信息管理数据库系统的流通子系统。这些数据是图书馆藏书量、服务效率在某个侧面的反映，通过这些数据可以分析出读者需求与倾向、阅读效果等活动规律，可为提高图书馆流通系统的管理水平提供科学依据。但是，与大多数的图书管理系统功能类似，这套系统可以利用后台数据库对图书馆的各种数据进行记录和管理，只能做基本的统计分析，无法对数据进行深层次的挖掘。因此，我们应用上述混沌预测模型对我院图书馆图书流通量行为中TP类图书在2003年1月至2010年12月间的流通量进行建模和预报。之所以选择中图法分类目录中TP类图书流通数据作为研究对象，是由于TP类图书为计算机与信息类图书，由于其应用的广泛性，较能代表医学专业学生的业余爱好和需求，可以作为学生综合素质的变化依据，因此有重要的参考意义。同时，从2003年到2010年，我院招生人数大幅攀升，目前已达两万余人，藏书量也有较快提高，人数的激增以及医学类就业形式的变化带来了图书流通量行为的巨大变化。论文分析使用的图书借阅流量时间序列如图1所示。

图1 图书借阅流量时间序列

3.2 模型学习

利用混沌时间序列分析与预测工具箱[5]计算得到上述数据的最大L y a p u n o v指数，为0.0163，说明该时间序列具有混沌性质，因此可利用上述混沌模型对该数据进行预测。首先选取2003年1月到2009年12月共84个月份的流通数据作为训练数据，2010年12个月份的数据作为测试样本。由于数据长度有限，未另外安排检测集。预测的步骤为：（1）归一化；（2）状态空间延迟重构；（3）支持向量机学习与预测；（4）数据处理与误差分析。

首先需要对数据进行归一化处理。归一化方式为：，使每一因子的数据都落入［0,1］区间。其次，由于混沌系统具有短期可预测性，因此可以按照式（1）的方式，通过引入延迟时间和嵌入维数，把一维时间序列改造成多维状态空间，以尽可能充分的提取原系统蕴藏的信息。嵌入维数m的选取成为关键。本文选择，延迟时间设为1，构建训练样本为。采用RBF核，使用Libsvm库[6]来做学习和预测。具体做法为，利用前84个训练数据重构得到80组训练样本，作为Libsvm的训练样本，利用Libsvm自带的网格法选取最优参数，其中以五折交叉验证作为评判标准，训练得到SVM模型，对第85个数据（即2010年1月份数据）进行预测，然后利用该预测值重新训练SVM模型，预测接下来的一个月份数据（类似于滑动窗口向后移动一位），依次递推直至完成。为衡量预测模型的精确性，采用相对误差：[4]

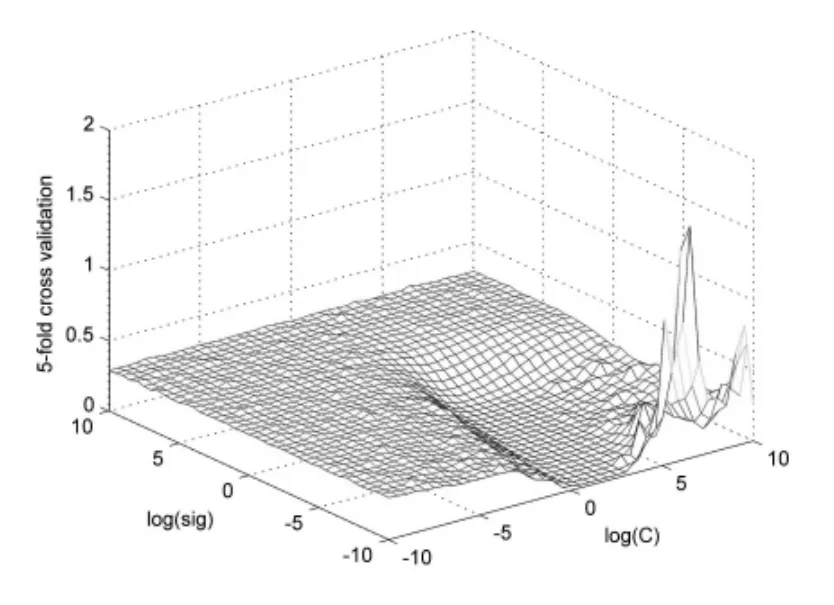
图2 网格法中不同参数对应的交叉验证值

图3 2010年图书借阅流量一步预测实际值与预测值的比较（相对误差err=0.0869）

图4 84个月份（2003.1～2009.12）数据的训练误差

由图3可知，利用基于支持向量机的混沌时间序列模型可较好地对2010年的流通数据进行预测，相对预测误差为8.69%。这表明本文所用方法是有效的，基本符合真实规律。同时，由图4可知，本文所用方法对建模所有的2003年至2009年间流通数据也达到了较好的拟合效果，只有一个月份的数据预测值达到59.06%，绝大部分月份的相对误差都低于20%。这充分表明本文所建立的混沌时间序列支持向量机模型是精确的，而且在嵌入维数没有经过严格筛选的情况下也能取得满意的预测效果。据分析，最主要的原因是支持向量机将人工重构的相空间进一步通过核函数映射到高维特征空间，从而克服非线性因素的干扰，并提取输入样本中包含的系统信息，从而带来良好的对未知数据的推广能力。

嵌入维数m对预测效果的影响较大。基于图2所得到的最优支持向量机参数，改变m，预测效果的变化如图5所示。可以观察到在嵌入维数小于5时，相对误差随着嵌入维数的增大而减小，这表明状态空间重构可以更好地表达时间序列内部的信息。在嵌入维数为5，6，7，8时，相对误差变化很小，而继续增加嵌入维数反而会导致相对误差有所上升。本文实验选择嵌入维数为5。这也契合了学生借阅行为的周期性，即寒暑假的借阅量往往会出现突变。

图5 图书借阅流量时间序列的嵌入维数与相对误差的关系

4 结语

采用量化方法研究图书馆服务与管理工作是当前图书馆学研究的趋势之一，有利于合理调配图书馆的人力物力，提高服务质量。图书借阅流量预测的意义在于，有助于对读者群体的需求进行评估，形成一定季节期限内的需求预测，在控制图书采编、藏书质量以及反馈服务质量上起重要作用。图书借阅流量行为具有明显的非线性非平稳的特性，因此采用传统的时间序列分析方法难以取得满意效果。本文采用支持向量机作为建模工具，引入了混沌时间序列预测模型，通过对图书借阅流量时间序列的分析和建模，从预测结果可以看出该模型具有较好的预测效果。笔者认为，任一时刻的借阅量数据的变化信息都隐含在与之相关的其他时刻的数据中。基于这种认识，本文所提方法的本质在于利用混沌时间序列的理论解释了图书借阅流量时间序列的变化，核心是利用状态空间重构提取了时间序列的内在信息，并建立了单步支持向量机预测模型。这种预测方法不会丢失时间序列中重要的周期信息（混沌的确定性），同时也充分考虑了借阅行为的突变性（混沌的长期不可预测性），从而避免了常规预报步数多、预报误差大的缺点。但由于分析中使用的借阅流量数据样本较少，在建立预测模型时无法充分表达图书借阅行为的信息。此外，外界因素的影响也应当加入到预测模型中。这些都是下一步工作中需要考虑的问题。

［1］姜炳蔚，任玉杰．回归分析在图书流通中的应用［J］.职大学报（自然科学版），2003（4）：6-7.

［2］吴红艳．图书借阅流量行为季节预测模型［J］.图书情报工作，2007，51（11）：98-101.

［3］V N Vapnik．The nature of statistical learning theory［M］．New York：Springer Verlag，1995..

［4］崔万照，等．混沌时间序列的支持向量机预测［J］．物理学报，2004，53（10）：3303-3309.

［5］陆振波．混沌时间序列分析与预测工具箱［EB/OL］.［2011-08-04］. http://luzhenbo.88uu.com.cn/.

［6］CC Change，CJ Lin．LIBSVM：a library for supportvector machine［EB/OL］.［2011-08-04］．http：//www.csie.ntu.edu.tw/cjlin/libsvm.