双脉冲发动机中金属膜片式隔舱设计方法①
2013-08-31刘伟凯
刘伟凯,惠 博
(1.西北工业大学燃烧、热结构和内流场重点实验室,西安 710072;2.航天动力技术研究院,西安 710025)
0 引言
双脉冲固体火箭发动机是固体火箭发动机的一项重大研究成果,其脉冲药柱具有独立的点火器,可以单独点燃,II脉冲药柱的点火时间可有不同的延迟[1]。目前,其推力向量控制和推力终止技术已得到较满意的解决,但仍存在一些问题需要进一步研究。文献[2]设计了一种软质隔层结构,利用扩展有限元技术研究了其在脉冲发动机中的承压和破坏过程,通过单项试验验证了数值仿真的准确性,说明其结构承压、打开及密封性能均满足设计要求,其结构可以应用于实际的脉冲发动机之中。文献[3-6]主要研究了双脉冲发动机的内流场特点:II脉冲工作时,由于级间通道的收缩导致燃气在I脉冲燃烧室产生后台阶流动,从而使燃气产生漩涡,强化了I脉冲的对流换热及粒子冲刷。
金属膜片式隔舱是利用轮辐式支撑件来减小重量,密封膜片与支撑件紧密贴实。为了减小打开压强,在金属膜片一侧设有预制缺陷槽,同时在金属膜片外侧附着一层绝热层进行绝热。由于该类隔舱兼具有结构设计简单、研制周期短、可靠性高等优点,在国际上被广泛应用于脉冲发动机领域[1]。
本文通过圆板大挠度理论和断裂力学理论推导出金属膜片预制缺陷处应力强度因子的计算式,从而得到金属膜片在内压作用下的设计方法。通过三维虚拟裂纹闭合法数值计算了预制缺陷处的应力强度因子并与公式计算结果对比,验证公式的准确性;通过推导多孔圆板关心区域的应力大小,得到支撑件强度校核方法。建立三维有限元模型,计算关心点的应力大小,验证校核方法的可靠性。最后通过实际的热流试验,验证了文中推导方法的有效性。
1 隔舱设计方法
1.1 隔舱物理模型
本文的金属膜片式隔舱与文献[7]保持一致,具体如图1所示,隔舱组件包括一个多孔支撑件和一个高强度易变形的金属模片。为了得到可靠的打开形式,预制缺陷槽(V型槽)一般设计为“十字型”或“米字型”,本文选取“米字型”预制缺陷膜片作为研究对象。为减轻支撑件重量以及增加通气面积,将支撑件设计为轮辐式结构。
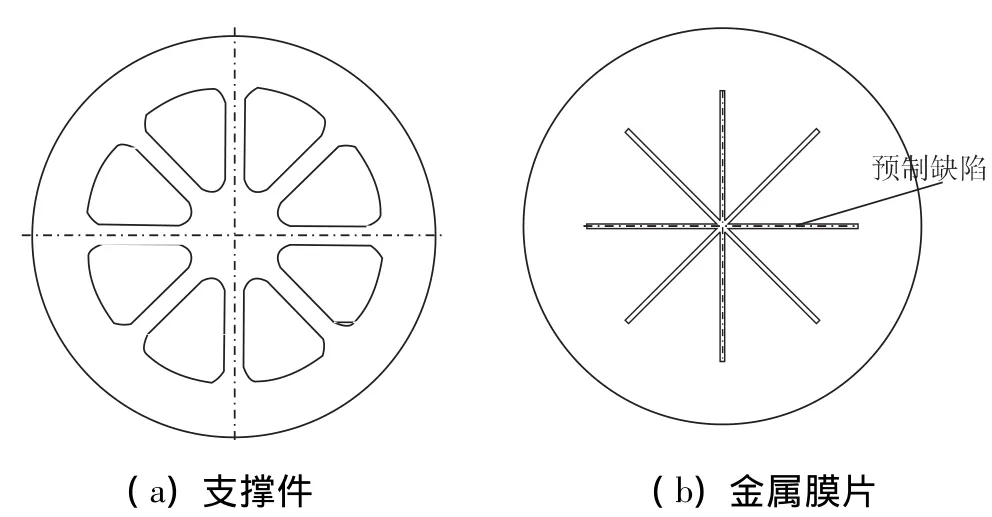
图1 金属膜片式隔舱结构Fig.1 Schematic diagram of metal diaphragm PSD
1.2 金属膜片设计式推导
为推导膜片预制缺陷处的应力强度因子,首先进行了如下假设:
(1)由于本文所设计金属膜片的预制缺陷槽为均匀放射状,各缺陷槽尺寸、受力状态完全相同,忽略各缺陷槽之间的影响,取其中任一条缺陷作为研究对象;
(2)结合前期摸底试验发现,本文的金属膜片破坏形式均为I型裂纹扩展破坏,因此本文只求解预制缺陷处的I型应力强度因子KI;
(3)本文选取垂直于缺陷槽的任一截面作为研究对象,由于垂直于截面上的应力对应力强度因子不产生影响,故将该截面简化为二维板条结构[8]。
(4)由于膜片实际破坏过程为瞬间动态过程,材料来不及发生塑性屈服,假设在破坏过程中材料都表现为线弹性属性,因此近似认为膜片的动态破坏过程为线弹性断裂问题。
为了量化膜片的破坏打开压强与膜片结构尺寸之间的关系,其中包括预制缺陷深度a、缺陷V型槽开口角度α、膜片半径R、膜片厚度h等。

本文将膜片承受燃烧室压强的变形过程简化为相同尺寸薄板(不含预制缺陷)的大挠度问题,圆板大挠度微分方程组如下[8]:
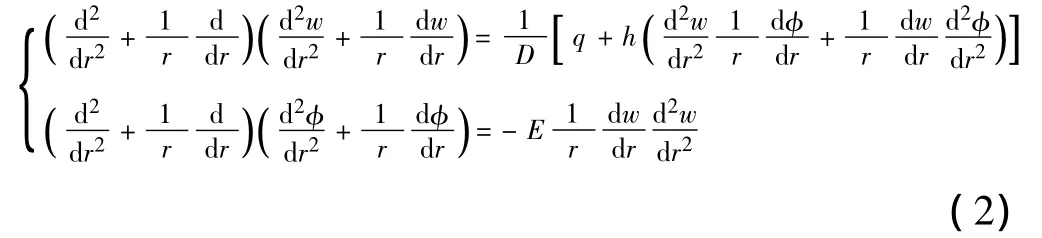
利用伽辽金法求解均布载荷下大挠度圆板应力场分布。设圆板的挠度符合式(3),把代入基本微分方程组(2)中,并结合圆板周边固定边界条件,得圆板中心的最大挠度计算式(4)。
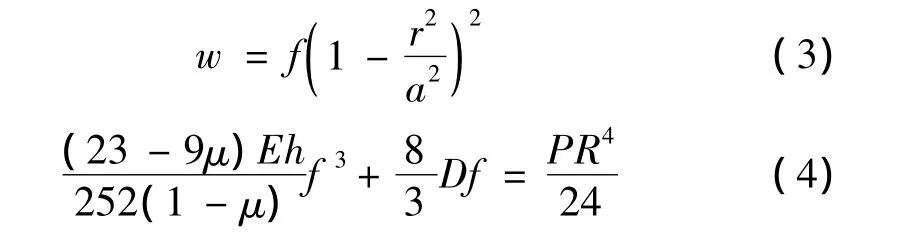
圆板任意点的切向应力包括两部分,即薄膜应力和弯曲应力,具体见式(5):
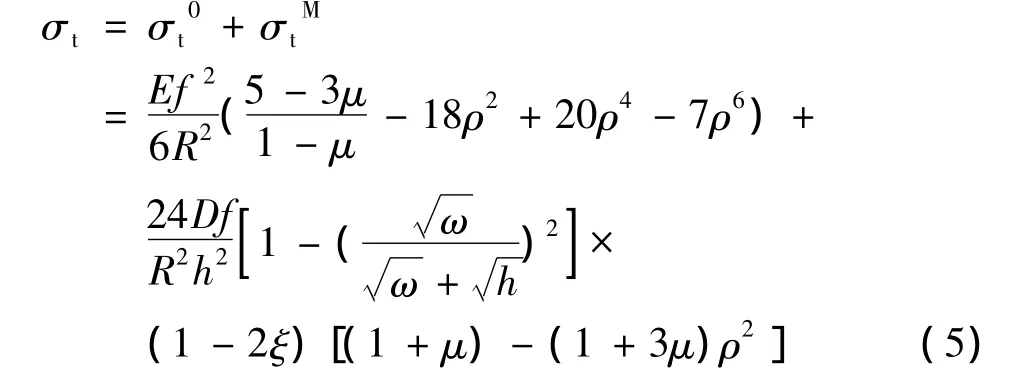
式中各参数具体含义与文献[7]相同。
通过式(5)即可计算得到预制缺陷相应位置的应力值,简化后截面应力分布如图2所示,利用叠加原理得到预制缺陷处应力强度因子的计算方法[7]。
通过叠加原理可得到中心处应力强度因子的计算式:

具体如下:

式中各参数具体含义与文献[7]相同。由于板中心的应力最大,所以预制缺陷中心位置的应力强度因子也最大,应力强度因子的分布形式如图3所示。
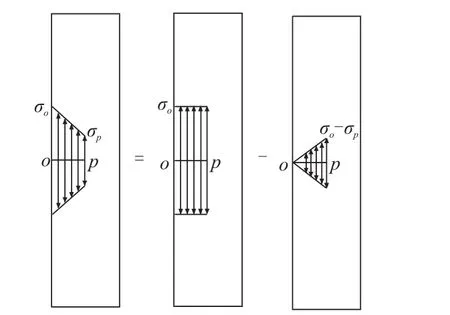
图2 应力强度因子叠加原理图Fig.2 Superimposed schematics of stress intensity factor
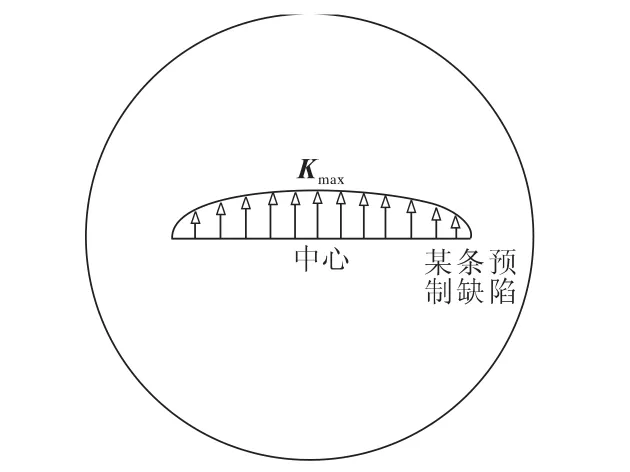
图3 预制缺陷处应力强度因子的分布Fig.3 Stress intensity factor distribution of the prefab defect
1.3 支撑件强度校核方法
支撑件为“多孔+轮辐”形式,计算其应力分布时需要将其简化为“当量无孔圆板”[9],此时需要对材料的弹性常数(E、μ)进行修正[9]。其应力的计算方法是:先应用一般实心圆平板的应力和变形公式,计算当量实心圆平板的应力和变形。再将当量实心圆平板的应力,乘以应力乘数和面积削弱系数,就可以得到多孔板的应力强度实际值,并以此作为强度计算的依据。
由于支撑件厚度较厚,承压变形过程中挠度较小,属于圆板的小挠度问题。首先将支撑件简化为周边简支的当量圆板,在均布压力P作用下,其上下表面的应力为
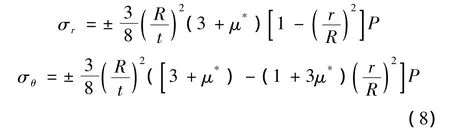
应力计算时,沿最小管孔带宽度方向取平均值,但并不沿板厚度方向取平均值,这时的有效应力为

式中 σave为由于外压载荷作用而产生的径向应力σr和环向应力σθ中最大者;κ=S0/S为实心圆板关心区域与有孔板关心区域面积与之比;K为应力乘数,无因次量[9]。
则支撑件强度校核方法:有效应力[σ]小于材料的强度极限σb。
2 数值计算验证
2.1 应力强度因子计算方法
虚拟裂纹闭合技术(VCCT)[10]最先由 Rybicki和Kanninen提出,用来计算二维裂纹问题,它通过对有限元分析结果进行后处理得到所需要的裂纹扩展的能量释放率;后被Shivakumar等推广至三维裂纹,在应用三维虚拟裂纹闭合法时,为了保证计算二维裂纹扩展的方法能够直接推广应用至三维裂纹,裂纹前缘处的网格应采用六面体单元。以有限块体中的裂纹(图4)为例介绍三维虚拟裂纹闭合法的原理,有限块体裂纹长度为a,裂纹扩展长度为Δa,网格采用8节点六面体单元,裂纹上表面节点和下表面节点一一对应,具有相同的坐标,则 I型、II型、III型应变能释放率 GI、GII、GIII可通过式(10)计算得到。
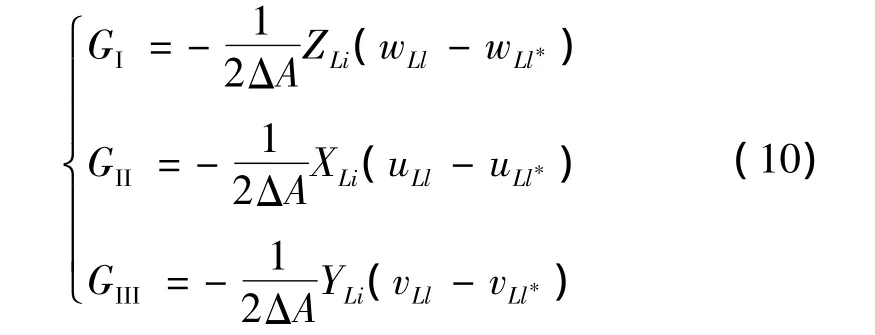
式中 XLi、YLi、ZLi分别为节点 Li 3个方向的节点力;wLl、uLl、vLl为节点 Ll 3 个方向的位移;wLl*、uLl*、vLl*为节点Ll*3个方向的位移;ΔA为单元裂纹面的面积;节点Ll和Ll*初始坐标相同。
需要指出的是,以上结果都是基于裂尖的局部坐标系所得到的结果,当裂尖的局部坐标系和全局坐标系不一致时,要将所有应力和位移转化到局部坐标系下。
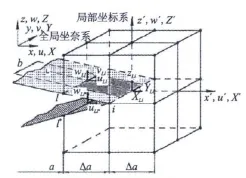
图4 三维裂纹示意图Fig.4 Diagram for G calculation by 3D-VCCT
在线弹性情况下,G和SIF有如下关系:
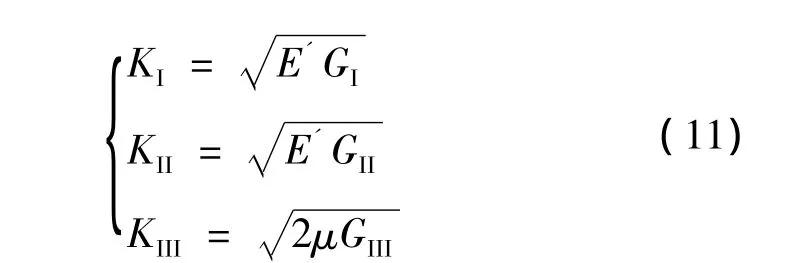
式中 KI、KII、KIII分别为裂尖处的 I型、II型、III型应力强度因子;对于平面应力状态E'=E;对于平面应变状态E'=E/(1-ν2);E为材料的弹性模量;μ为材料的剪切模量。
ABAQUS已将VCCT功能集成到有限元程序中,本文直接利用ABAQUS的3D-VCCT计算功能,不需用户子程序开发就可以得到满意的计算结果。
2.2 计算模型
建立简化后的金属膜片的三维有限元模型,为简化计算、有利于网格的划分,简化金属膜片只有一条预制缺陷。合理简化边界条件,模拟膜片在发动机中的实际连接形式。整个膜片全部采用结构化网格,单元类型为C3D8R,单元总数为3.5万。具体计算模型如图5所示,膜片的材料选用LY12超强铝合金。
将整个加载过程定义为静态分析步:在隔膜片II脉冲一侧施加压力载荷,模拟II脉冲燃烧室初始工作压强,分析步为静态分析步,载荷的大小随时间线性增加,计算预制缺陷在2.0 MPa下的应力强度因子。
建立支撑件及膜片的三维有限元模型及相应当量实心圆板三维有限元模型,在膜片一侧分别施加压力载荷,研究支撑件及实心圆板中心受拉一侧应力变化情况。三维有限元模型如图6所示,边界条件为简支,单元类型为C3D8R减缩积分单元,单元总数为20万。
图5 带1条预制缺陷的圆平板模型Fig.5 Circular plate model with one prefab gap

图6 有限元计算模型Fig.6 Finite element model
3 公式解与数值计算结果对比
3.1 膜片的应力强度因子对比
根据式(7)计算预制缺陷上的应力强度因子分布,并与有限元计算结果对比如图7所示。
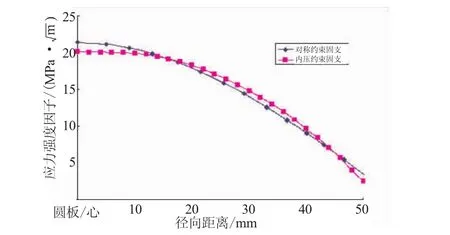
图7 公式与数值计算结果对比Fig.7 Formula and numerical calculation results
对比图7可知,2种方法计算的应力强度因子变化趋势一致,在圆板中心位置达到最大,沿径向方向逐渐减小,与图3定性分析结果一致。同时,二者之间存在一定差异,在圆心位置公式计算结果为21.4 MPa·,数值计算结果为20.1 MPa·,误差为 6.5%。在预制缺陷末端公式计算结果为3.4 MPa·,数值计算结果为2.5 MPa·,误差达到34.2%。
分析认为,造成二者之间主要差别的原因是:
(1)公式的假设引入误差。公式推导过程中作了大量假设,如假设所取截面为二维平面应变结构,必然会引入一定的误差。
(2)数值计算结果对模型敏感。利用有限元数值计算裂纹应力强度因子时,计算结果对网格尺寸及裂纹前缘选取较为敏感,不同的网格划分形式,及不同的裂纹前缘选取都会导致数值计算结果的差异(本文计算时选取裂纹前缘与裂尖一致)。
由于本文所设计的膜片结构破坏过程都是从圆心位置最先达到材料的断裂韧性,从中心开始破坏,并扩展致整个预制缺陷。如果材料的断裂韧性为20 MPa·,则根据公式及数值计算结果,在2 MPa内压作用下,膜片已经从中心位置破坏。
3.2 支撑件的应力大小对比
计算所得到各点的最大主应力,其中实心圆板的应力按式(8)计算,支撑件的应力按式(9)计算。由于本文主要关心圆板中心的应力状态,在计算S0/S比值时,按图8所示的2个面积进行计算,S0/S≈2,将公式计算结果与有限元计算结果对比如图9所示。如图9所示,公式计算结果与有限元计算结果保持一致,变化趋势相同,但略高于有限元计算结果,说明利用该方法进行强度校核时,所得结果偏于“保守”,有利于提高隔舱整体的承载能力。
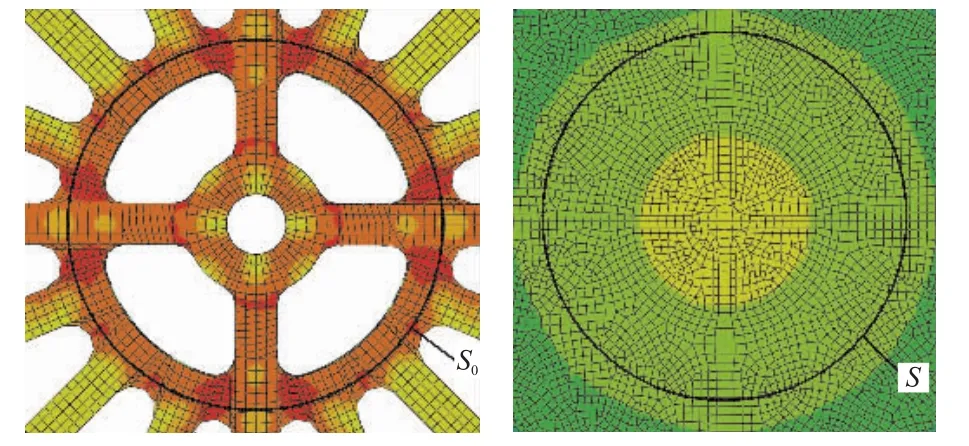
图8 关心区域对应的面积Fig.8 The areas of interest region
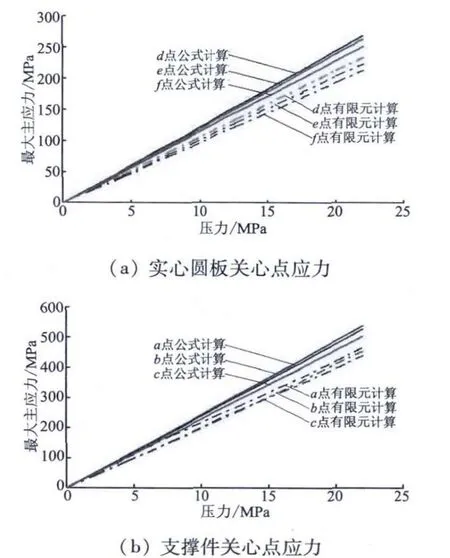
图9 不同压力下计算结果对比Fig.9 Calculation results under different pressures
4 验证试验
4.1 膜片的打开压强验证试验
考虑到某双脉冲发动机的直径,同时保证II脉冲药柱能稳定点燃(一般要求初始压强控制在1.5~2.5 MPa),本文设计II脉冲初始工作压强为2.0 MPa,根据前文设计公式,设计膜片具体尺寸如下:制缺陷深度a=1 mm,缺陷V型槽开口角度α=π/2,膜片半径R=142 mm,膜片厚度h=3 mm。
本文进行了5次膜片的破坏打开单项试验[7],膜片的打开压强分别为:2.30、1.90、2.33、2.00、1.95 MPa。膜片的平均打开压强为 2.1 MPa,比公式计算结果2.0 MPa高约5%。可见公式计算结果可较好预测膜片的真实动态打开压强。
4.2 支撑件强度校核试验
考虑到某双脉冲发动机I脉冲的实际工作压强为16 MPa,本文隔舱的承压极限要求大于22 MPa,利用式(9)对前期的多种结构形式及材料的支撑件进行强度校核,最终确定支撑件的结构形式如图6(a)所示,材料为LC9超强铝合金,隔舱整体厚度为20 mm,根据式(9)隔舱的极限承载压强为24 MPa。
本文对该隔舱进行了热流承压试验,试验装置为模拟发动机,由于试验成本较高,本文只进行了3发承压试验,发动机工作压强分别为 21.5、22.3、20.5 MPa。试验完成后,拆分模拟发动机,观察支撑件一侧,发现支撑件结构完整。说明本文的强度校核方法可以较好的预示隔舱的承载极限,为隔舱的设计提供一定依据。
5 结论
(1)根据本文推导的公式计算预制缺陷上的应力强度因子分布,与有限元计算结果一致性较好,在圆心位置公式计算误差仅为6.5%。根据公式预估结果,膜片的破坏压强为2.0 MPa,金属膜片5次试验的平均打开压强为2.10 MPa,公式误差仅为5%,进一步验证了公式的准确性。
(2)根据支撑件强度校核公式得到的关心点的应力值略高于有限元计算值,说明校核公式更偏于保守。通过热流承压试验,验证了隔舱的承载性能,进一步说明本文所推导公式可以用来校核隔舱支撑件的强度,得到隔舱极限承载压强。
(3)本文利用圆板大挠度理论及断裂力学理论,得到了金属膜片的设计公式,公式计算所得到的打开压强可以用来预估膜片的真实打开压强。利用多孔圆板理论,得到支撑件强度校核方法,可以用来对支撑件结构形式及材料进行前期优选。本文得到的公式可以为双脉冲发动机中隔舱设计提供参考依据。
[1]Wang Chun-guang,Liu Hong-chao,Yang De-min.Study of development status and future development proposals for pulse soild rocket motor[J].Applied Mechanics and Materials,2012(110-116):2354-2358.
[2]王春光,田维平,任全彬.脉冲发动机中隔层工作过程的数值分析及试验[J].推进技术,2012,33(5):790-794.
[3]孙娜,娄永春,孙长宏.某双脉冲发动机燃烧室两相流场数值分析[J].固体火箭技术,2012,35(3):335-338.
[4]刘亚冰,王长辉,刘宇.双脉冲发动机燃烧室局部烧蚀特性分析[J].固体火箭技术,2010,33(4):453-456.
[5]曹熙炜,刘宇,任军学.内孔隔板脉冲固体火箭发动机流场分析[J].航空动力学报,2011,26(2):448-452.
[6]朱卫兵,张永飞,陈宏.双脉冲发动机内流场研究[J].弹箭与制导学报,2012,32(1):114-118.
[7]王春光,任全彬,田维平,等.脉冲发动机中金属膜片式隔舱动态破坏过程研究[J].固体火箭技术,2013,36(1):573-577.
[8]刘鸿文.板壳理论[M].浙江大学出版社,1987.
[9]谢桂兰,张平,龚曙光.基于均匀化理论的管板有效弹性常数的研究[J].应用力学学报,2004,21(3).
[10]解德,钱勤,李长安.断裂力学中的数值计算方法及工程应用[M].北京:科学出版社,2009.
