基于能量守恒的复合固体推进剂粘弹性本构关系①

龚建良，刘佩进，李 强

(西北工业大学燃烧、热结构与内流场重点实验室，西安 710072)

0 引言

复合固体推进剂作为固体火箭发动机的重要能源物质，要求其具有一定的力学性能。一般复合固体推进剂的粒子体积分数高达80%，是一种粒子增强体复合材料，力学特性复杂，出现多种现象，如应变软化、Mullin效应、界面脱湿及体积膨胀等［1］。在化学性能不变的情况下，这些力学现象是多种因素综合作用的结果，可将其影响因素分为3种:一是几何因素，如粒子体积分数﹑粒子的几何形状﹑粒径分布﹑颗粒的聚集程度等;二是物理因素，如基体的物理属性、粒子的物理属性、粒子与基体的界面粘结特性;三是环境因素，如温度、载荷速率、围压等。在这些因素共同影响下，复合固体推进剂内部出现的损伤，如基体裂纹、粒子断裂、基体与粒子的界面脱湿，使得其力学性能从线粘弹性转为非线性粘弹性，对正确预估其力学性能提出困难。文献［2］与［3］分别从试验与理论上，确定了在复合固体推进剂中主要损伤形式是粒子与基体的界面脱湿，并对其宏观力学行为具有重要影响。特别对其研究方法，不能局限于传统的宏观力学水平，由于颗粒﹑界面的尺度都处于微米级别，涉及到细观尺度。因此，研究中应充分考虑细观现象对其宏观性能的影响，有必要建立一种宏细观结合的粘弹性本构关系。

复合固体推进剂是一种粒子增强的复合材料，主要由聚合物基体与刚性的氧化剂粒子组成［1］。国外，针对复合固体推进剂，Schapery从不可逆热力学角度，引入2个内变量描述复合固体推进剂的损伤，提出了宏观形式的本构关系［4］。Vratsanos与Farris从能量守恒角度，假定粒子的脱湿是从大粒子到小粒子依次脱湿，认为粒子的脱湿是导致复合固体推进剂非线性的主要原因，并确定了宏观本构关系［5］。Jung从粘弹性角度，假定基体粘性不改变粒子的脱湿过程，建立了临界脱湿应力方程，利用微分方程计算了宏观有效割线模量，并结合Simo粘弹性本构关系，描述了复合固体推进剂的力学性能［4，6］。Ravichandran与 Liu基于 Eshelby等效夹杂理论与Mori-Tanaka方法，考虑了复合固体推进剂中的界面损伤，提出了一个率无关的唯象本构关系［7］。Tan针对PBX9501高能炸药，使用数字图像相关(DIC)技术，获取了基体与粒子的界面粘性定律，并确定了模型参数，并在RVE上，使用平均化与Mori-Tanaka法，确定了高三轴应力下的线弹性宏观本构关系，利用有限元技术数值模拟了宏观本构关系，显示了增强体粒径大小对PBX9501高能炸药的界面脱湿具有重大影响，并将此模型扩张到线粘弹性本构关系［3，8－9］。国内，陈建康针对粒子增强体粘弹性复合材料，使用Eshelby等效理论与Mori-Tanaka法，建立了宏观本构关系，通过数值模拟得出了宏观应变率、粒子分散度、基体的松弛时间与界面粘结强度对宏观本构关系都具有重大影响［10］。彭威针对复合固体推进剂，考虑粒子增强作用与界面脱湿损伤，建立了含损伤变量的粘弹性宏观本构关系，并与拉伸曲线对比，结果吻合较好［1］。李丹与胡更开针对高粒子体积分数聚合物材料，基于Laplace变换和双夹杂相互作用的弹性模型，建立了细观力学模型，计算了玻璃珠/ED-6复合材料的有效松弛模量及常应变率下的本构关系［11］。赵玖玲针对复合固体推进剂的界面脱湿机理，建立了双尺度有限元损伤分析平台，分析了在小应变范围内的宏观应力应变曲线，得到了界面脱湿使推进剂的宏观模量降低［12］。

从以上研究可看出，针对复合固体推进剂的力学性能，国内外已从细观力学角度展开研究。然而，在大应变载荷时，界面脱湿对宏观力学行为具有重要影响，需要深入地定量分析。因此，本文针对聚合物基复合固体推进剂，采用横观各向同性的空泡(Vacuole)代替已发生脱湿的AP粒子，基于能量守恒定律与细观有效场理论，推导了一种宏细观结合的粘弹性算法。采用Fortran语言完成程序的编写，针对单峰分布的配方与双峰分布的配方推进剂，数值计算了拉伸曲线，定量分析了界面脱湿对其粘弹性力学性能的影响，为预估推进剂配方在大应变载荷时的力学性能，提供了一种精确与稳定的工具。

1 建立宏细观结合的粘弹性算法

在载荷作用下，假设复合固体推进剂内部粒子从大到小依次发生界面脱湿，采用能量守恒方法得到了在粒子发生脱湿后的临界应变方程，并依据细观理论Ju-Chen方法，估计了在临界应变方程中的宏观有效模量。最后，采用三参数Poything模型，描述了复合固体推进剂的粘弹性。在复合固体推进剂所有内部粒子的脱湿过程中，通过循环迭代，建立了宏细观的粘弹性算法。

首先，依据能量守恒定律，假设其内部损伤完全由界面脱湿决定，得到了在粒子发生脱湿后的临界应变方程［6］:

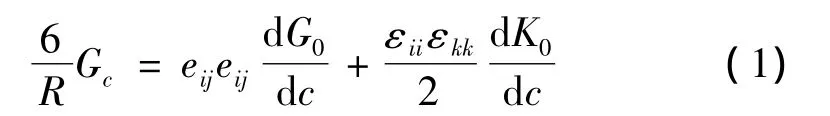
式中 Gc是基体/粒子单位面积的界面粘结能，R是粒子的半径，c是粒子体积分数，G0与K0分别是复合固体推进剂宏观有效剪切模量与体积模量。

应变偏量eij与体量εkk满足:

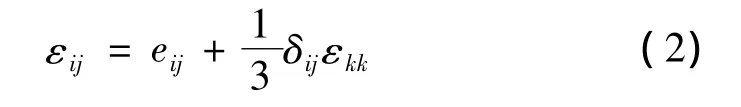
可知，式(1)描述了复合固体推进剂在粒子发生脱湿后，临界应变与宏观有效模量、粒子半径、粒子体积分数及界面粘结能的关系。

其次，采用了Ju-Chen方法确定临界应变方程的宏观有效模量。由扫描电镜结果可知，复合固体推进剂在拉伸过程中存在基体/粒子的界面脱湿，并产生空泡，粒子的增强效果减弱［2］。因此，粒子在发生脱湿后，采用空泡描述其状态，见图1。图1描述的是一种由粒子、空泡与基体组成的三相复合材料。为了确定细观尺度的粒子对复合材料的宏观增强效果，采用Ju-Chen方法，预估了含空泡的三相复合材料的宏观有效模量。设复合材料平均刚度矩阵是［¯C］，基体刚度矩阵是［C0］，粒子刚度矩阵是［Ci］，以及由粒子脱湿而产生的空泡刚度矩阵是［cv］，有如下关系［13］:

式中 ［］方括号表示方阵;［A］=［Ci－ C0］－1［C0］，［B］=［Cv－C0］－1［C0］;ci为粒子的体积分数，cv为由粒子脱湿而产生的空泡体积分数;［S］为Eshelby矩阵［13］。

图1 三相复合材料Fig.1 Three-phase composite

在载荷作用下，脱湿的粒子并不是完全地散失载荷传递能力，不同部位脱湿程度不同，一般是从极区开始脱湿。因此，引入因子Fb表示不同的脱湿程度，认为脱湿的粒子，即空泡，具有横观各向同性属性，其刚度矩阵表示为［14］

式中 m=(1－ν23ν32)－1;Eii为弹性粒子的弹性模量;νij为弹性粒子的泊松比。

为了考虑相与相的相互影响，式(3)中的［Γr］表示相互影响矩阵，当r=i表示粒子;当r=v表示空泡，相互影响矩阵表示为［13］

式中 ［I］为单位方阵;cr为相 r的体积分数;Y=Ym(1－cr)，Ym为相互影响系数;［Wr］= ζ1δijδkl+ζ2(δikδjl+ δilδjk)，包括参数 ζ1，ζ2，β。

最后，复合推进剂在载荷作用下的力学响应是粘弹性，如果采用细观力学有效场理论确定粘弹性复合材料的有效模量，需要使用Laplace变换原理，这涉及频率域到时间域的逆变换，过程复杂，甚至不存在逆变换。因此，本文将粘弹性的力学响应分为弹性响应与粘性响应，弹性响应使用Ju-Chen方法确定，而粘性响应使用3参数Poything模型描述［15］，在恒温常拉伸速率载荷下，复合固体推进剂的粘弹性宏观本构关系是:

式中 E0是瞬时弹性响应模量，由等式(3)确定;参数E1与τ分别是复合固体推进剂的松弛模量与松弛时间。

至此，完成了宏细观结合的界面脱湿粘弹性算法的建立。为了将算法应用于复合固体推进剂力学性能的预估，采用Fortran语言编制了程序，程序的流程结构见图2。

图2 粘弹性算法的流程图Fig.2 Flow chart of viscoelastic algorithm

2 界面脱湿粘弹性算法的验证

为了验证算法的正确性，针对单峰分布的HTPB基玻璃珠增强复合材料展开数值模拟，算法中的原始参数依据文献［14］的实验结果而确定。平均粒径32 μm，对数标准差0.167;初始粒子体积分数Fi=30%，初始的空泡体积分数Fv=0。拟合确定界面粘结能Gc=2.24 J/m2，部分脱湿因子 Fb=10－5，相互影响系数Ym=1.18。依据文献［14］玻璃珠增强粒子的剪切模量Gi=30 GPa与泊松比 νi=10－5，基体的泊松比 ν0=0.495，基体的瞬时弹性响应模量 E0=1.55 MPa［14］。

给定控制体的体积是4 609 mm3，在控制体中内粒子的频度分布依据实验结果而确定。由文献［14］可知，粒子的频度满足对数正态分布，图3显示了在数值模拟中控制体内粒子的频度分布，平均粒径32 μm，最小粒径 1 μm，最大粒径113 μm。

在拉伸速率10 mm/min、有效距离75 mm载荷下，文献［14］获取了模拟复合固体推进剂HTPB的拉伸曲线，应用本文算法在相应的应变率˙ε=0.002 2 s－1下，松弛模量 E1=0.2 E0，松弛时间 τ =120 s，通过数值模拟获取计算结果，并与文献［14］的实验数据相对比，见图4。结果表明，计算结果与实验数据较为吻合，说明了假定粒子从大粒径到小粒径粒子的脱湿过程是合理的，且拉伸曲线由线粘弹性阶段与非线性软化阶段组成。

图3 控制体中粒子的频度分布Fig.3 Frequency distribution of particles on the ensemble-volume

图4 针对HTPB基复合材料，数值模拟与试验数据对比Fig.4 Comparison between computation and experiment for composite based HTPB

3 数值模拟的分析

3.1 界面粘结能对粘弹性力学性能的影响

为了确定基体与粒子的界面粘结能力对复合固体推进剂宏观力学行为的影响，针对单峰分布的HTPB基玻璃珠增强复合材料，采用第2章的初始参数，计算了不同界面粘结能的拉伸曲线，见图5。可知，随着界面粘结能的增大，临界应变随之增大，推进剂的强度提高，具有更高的承载能力。因为临界应变方程表明了临界应变与界面粘结能的平方根成正比，所以在推进剂配方中，增加基体与粒子界面的粘接能力，可提高力学性能。但也可看出，在拉伸曲线的初始阶段，界面粘接能不影响拉伸曲线的性能，因为在此阶段基体与粒子界面粘接良好，所以获得相同的拉伸曲线。

3.2 拉伸速率对脱湿与力学性能的影响

为了分析拉伸速率对复合固体推进剂脱湿与力学性能的影响，针对单峰分布的HTPB基玻璃珠增强复合材料，采用第2章的初始参数，计算了在不同拉伸速率下的拉伸曲线，见图6。可知，拉伸速率越高，初始宏观有效模量上升，粒子内部更容易发生界面脱湿。因为拉伸速率的提高，改变了载荷对复合材料的作用时间，载荷速率越高，作用时间越短，粘弹性基体显示出脆性。

图5 界面粘结能对宏观力学行为的影响Fig.5 Influence of interfacial adhesive energy on macroscopic mechanical behavior

图6 不同拉伸速率下的计算拉伸曲线Fig.6 Calculation curves for different tension rates

3.3 体积分数对脱湿与力学性能的影响

针对简化配方的双峰分布HTPB基复合材料，依据文献［12］的 AP 粒径峰值是 335 μm 与 135 μm;在不影响粒子增强效果与界面损伤情况，忽略小组分等微量元素;应用本文算法取Gc=11.2 J/m2，分别计算了粒子体积分数47%﹑55%与59%的拉伸曲线，见图7。由图7可知，粒子体积分数的增大，初始宏观有效模量值随之增大，宏观强度也得到提高。但当界面发生脱湿后，复合固体推进剂内部粒子发生而出现空泡，宏观有效模量发生退化，拉伸曲线发生线粘弹性转化为非线性粘弹性的现象，体积分数越高，产生空泡的机会也就越高，力学性能更容易出现软化行为。为了进一步说明在高粒子体积分数的推进剂中更容易发生损伤。图8为不同体积分数下的体积膨胀应变行为。

图8计算了在拉伸过程中相应的体积膨胀应变。可知，体积分数越高，体积膨胀应变越大，表明了推进剂内部损伤程度严重，也说明了界面发生脱湿后，推进剂从不可压向可压缩性质转变。表1给出了Ju-Chen方法预估复合材料的初始模量值。可知，本文的预估精度高于文献［12］。

图7 不同体积分数下的力学行为Fig.7 Mechanical behaviors for different particle volume fraction

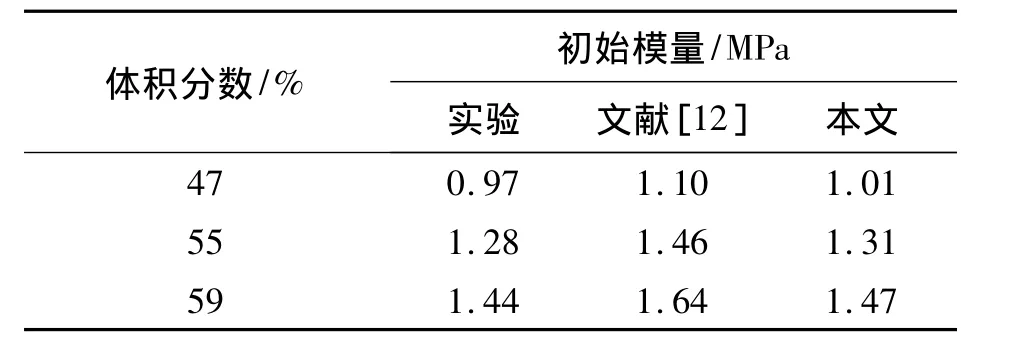
表1 HTPB初始模量Table 1 Initial Modulus for HTPB

图8 不同体积分数下的体积膨胀应变行为Fig.8 Dilatation strain behaviors of different particle volume fractions

4 结论

(1)针对复合固体推进剂在几何因素与物理因素确定的情况下，只要给定了粒子与基体的界面粘结能，就可直接应用本文算法，分析在大应变载荷时界面脱湿对其粘弹性本构关系的影响。

(2)粒子体积分数对宏观力学行为具有重要影响，高粒子体积分数可增强强度，但拉伸曲线的软化行为更加明显。

(3)增加界面粘结能，可对粒子的脱湿起到抑制作用。但随拉伸速率的提高，界面更容易脱湿。

［1］彭威.复合固体推进剂粘弹损伤本构模型的细观力学研究［D］.长沙:国防科技大学，2001.

［2］曾甲牙.丁羟基推进剂拉伸断裂行为的扫描电镜研究［J］.固体火箭技术，1999，22(4):328-334.

［3］Tan H，Huang Y，Liu C，et al..The Mori-Tanaka method for composite materials with nonlinear interface debonding［J］.International Journal of Plasticity，2005，21(10):1890-1918.

［4］Schapery R A.A micromechanical model for non-linear viscoelastic behavior of particle-reinforced rubber with distributed damage［J］.Engineering Fracture Mechanics，1986，25(5):845-867.

［5］Vratsanos-Anderson L L，Farris R J.A predictive model for the mechanical behavior of particulate composites.Part I:Model derivation［J］.Polymer Engineering ＆ Science，1993，33(22):1458-1465.

［6］Jung G D，Youn S K.A nonlinear viscoelastic constitutive model of solid propellant［J］.International Journal of Solids and Structures，1999，36(25):3755-3777.

［7］Ravichandran G，Liu C T.Modeling constitutive behavior of particulate composites undergoing damage［J］.International Journal of Solids and Structures，1995，32(6):979-990.

［8］Tan H，Liu C，Huang Y，et al..The cohesive law for the particle/matrix interfaces in high explosives［J］.Journal of the Mechanics and Physics of Solids，2005，53(8):1892-1917.

［9］Tan H，Huang Y，Liu C.The viscoelastic composite with interface debonding［J］.Composites Science and Technology，2008，68(15):3145-3149.

［10］Chen J K，Huang Z P，Mai Y W.Constitutive relation of particulate-reinforced viscoelastic composite materials with debonded microvoids［J］.Acta Materialia，2003，51(12):3375-3384.

［11］李丹，胡更开.高体积百分比颗粒增强聚合物材料的有效粘弹性性质［J］.应用数学和力学，2007，28(3):270-280.

［12］赵玖玲，强洪夫.基于粘附功的复合推进剂AP/基体界面损伤宏细观仿真［J］.固体火箭技术，2011，34(5):614-618.

［13］Ju J W，Chen T M.Effective elastic moduli of two-phase composites containing randomly dispersed spherical inhomogeneities［J］.Acta Mechanica，1994，103(1):123-144.

［14］Wong F C，Kadi A A.Predictive capability of a new Mori-Tanaka micromechanical model for particulate composites［R］.AIAA 98-1861.

［15］张义同.热粘弹性理论［M］.天津:天津大学出版社，2002:53-139.