摆动喷管控制导弹鲁棒飞行控制系统设计①

朱学平，祁 鹏，张晓峰，杨 军

(1.西北工业大学航天学院，西安 710072;2.第二炮兵驻航天科技集团公司四院军事代表室，西安 710025;3.中国兵器工业第203研究所，西安 710065)

0 引言

高速、大机动飞行器的迅速发展，对防空导弹飞行控制技术提出了更高要求。传统气动力控制的防空导弹很难满足快速、大机动拦截、高精度命中的要求。推力矢量控制是一种通过控制主推力相对弹轴的偏转产生改变导弹姿态所需力矩的控制技术。显然，这种控制方法在低速、高空状态下仍可产生很大的控制力矩。推力矢量控制具有气动力控制不具备的优良特性。因此，在现代导弹设计中，特别是在垂直发射地空导弹、弹道导弹及大离轴发射空/空导弹设计中得到了广泛应用。

摆动喷管通过改变沿轴向喷出的气流方向，可获得较大的俯仰/偏航力矩，同时推力损失小，这种良好的燃气动力品质已受到防空导弹的青睐［1］。某防空导弹拟采用弹轴摆动喷管实施俯仰和偏航方向的控制，用于弹体垂直发射转弯飞行和主动段飞行。由于防空导弹传统的操纵机构是空气舵/燃气舵，对于摆动喷管的知识储备非常少。因此，对于摆动喷管控制导弹，在飞行控制系统综合时，必须充分考虑摆动喷管的控制偏差，设计出具有强鲁棒性的飞行控制系统。

本文将参数空间方法和定量反馈理论(QFT)［2－3］应用到摆动喷管控制防空导弹飞行控制系统设计中，考虑摆动喷管的控制偏差，分析了飞行控制系统的鲁棒性，取得了良好效果。

1 摆动喷管控制导弹弹体数学模型

考虑摆动喷管的摆尾效应，建立摆动喷管控制导弹纵向刚体扰动方程:

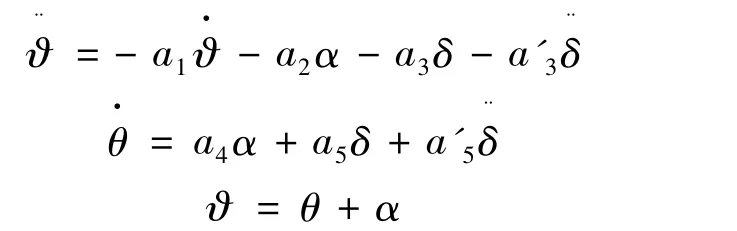
式中 ϑ为弹体俯仰角;α为攻角;θ为弹道倾角;δ为舵偏角;a1～a5，a'3，a'5为动力学系数，其定义参见文献［4］。

摆动喷管在非理想状态下摆动时，作动器牵连运动、正负摆角不对称、力臂变化、摆心漂移、位移传递系数精度和预调角对摆角控制会产生影响;同时，负载力矩和伺服机构相关参数影响着摆动喷管位置控制精度［5］。

摆动喷管执行机构的线性化数学模型为

其中，T=0.005 s，ξ=0.6。

摆动喷管控制导弹气动参数的不确定性及摆动喷管的控制误差，用相关动力学系数的相对误差表示。主要考虑的误差项及误差范围为

摆动喷管控制导弹飞行控制系统综合时，需保证上述偏差条件下系统的鲁棒性能。本文基于参数空间方法和定量反馈理论，完成了喷管控制导弹鲁棒飞行控制系统设计。

2 参数空间方法和定量反馈控制理论

2.1 参数空间方法

(1)多模理论

设一个状态空间模型为

式中 θ是不确定对象参数向量。

假设期望的反馈控制律为

需要解决的鲁棒性问题是寻找反馈增益矩阵，使得u(t)=－Kx时，系统对所有的θi均能满足性能指标要求。多模方法解决这个问题的思路是:如果可得到有限个模型(取常值 θ1，θ2，…，θn)，在这种情况下，使所有模型都稳定的 K 值是 θ=θ1、θ=θ2、…、θ=θn投影到K-空间的稳定域的交集，这种方法就是“多模方法(Multi-model Approach)”。

(2)区域极点配置

对于单输入单输出系统:

其中，(A，b)可控。设计状态反馈控制律:

这样闭环系统:

有一个规定特征值集合 s1，s2，…，sn，闭环系统特征多项式为区域极点配置的概念是将所有极点配置在复平面的一个Γ区域，位于Γ区域的极点可使系统具有合适的性能。在θi已知的情况下，反馈增益矩阵K所在的空间中，存在一个KΓ区域与Γ区域对应。对于不同的 θi设计 KΓj，则模型族公共控制器是交集KΓj。图1给出了2个对象情况区域极点配置示意图。

图1 区域极点配置示意图Fig.1 Region pole assignment

2.2 定量反馈理论

2.2.1 QFT 的控制系统结构

QFT一般的设计结构为如图2所示的一种二自由度系统。图2中，{P}为带有不确定性的被控对象;G和F分别为要设计的控制器和前置滤波器;d1和d2分别为外部输入干扰和输出干扰。

2.2.2 性能指标与边界

QFT设计是在Nichols图上进行的，它的基本设计思想是先将对闭环系统的设计要求转化为在Nichols图上对基准对象开环频率响应曲线进行约束的一系列边界，然后通过调整基准对象的开环频率响应曲线，使得其满足边界条件来设计控制器G。针对控制系统要求，QFT的一般设计指标包括稳定性和稳定裕度指标、跟踪性能指标等。

图2 二自由度控制系统结构图Fig.2 Structure of the two-DOF control system

(1)鲁棒稳定性(Robust stability)

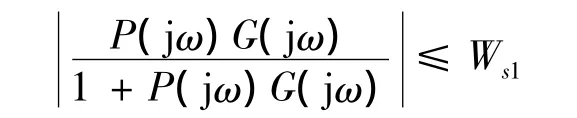
(2)跟踪性能指标(Tracking performance)

式中 α(jω)和 β(jω)分别为给定的跟踪特性下界和上界。

将闭环系统的设计要求转化为在Nichols图上的边界，包括鲁棒稳定边界和跟踪边界等。

(1)鲁棒稳定边界

稳定边界保证标称对象的开环频率曲线不与临界点(在Nichols图上为(－180°，0 dB))相交，且有一定的区域限制范围。稳定边界在Nichols图上一般是一些闭环曲线。

(2)跟踪边界

在控制器G(s)的作用下，闭环系统的传递函数为

由系统的闭环传递函数可知，闭环传递函数T的不确定性只取决于L(或P)的不确定性，即

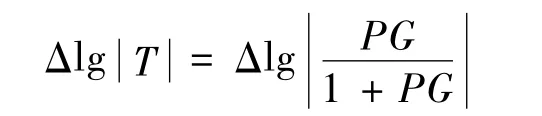
在选定跟踪边界的上界β(jω)和下界α(jω)后，对于任意频率ω和控制对象其中某一对象P∈{P}，加入控制G和前置滤波器F。则有

即

上式可变换为

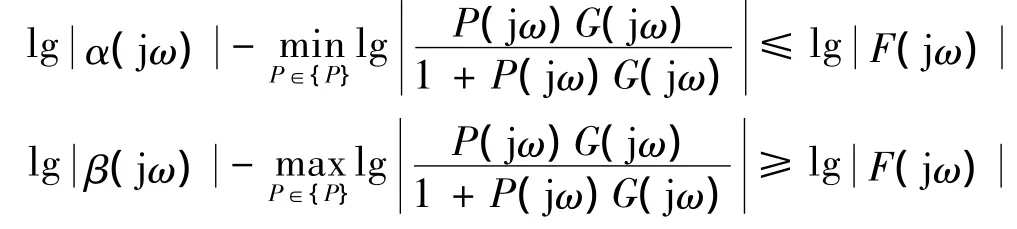
因此

对于QFT而言，控制器G和前置滤波器F的设计可独立进行，从而降低了设计的复杂性。

2.2.3 控制器和前置滤波器设计

由于QFT是一种图形设计方法，所以控制器G的设计过程也叫回路成形过程(Loop Shaping)。在绘有复合频域边界的Nichols图上，作出标称对象的开环频率响应曲线 L0(jω)，由于

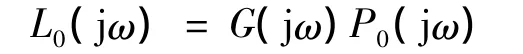
可知，当G含有零极点或增益时，可调整L0(jω)的位置和形状。前置滤波器F作用是调整系统的整体频率响应特性，使闭环的频率响应满足上下边界要求。加入前置滤波器F后，系统的传递函数为

则

根据式(3)频率响应边界来计算前置滤波器。

3 鲁棒飞行控制系统设计与仿真分析

摆动喷管控制导弹俯仰通道法向过载飞行控制系统采用如图3所示的三回路结构形式。

本文基于参数空间方法，完成伪攻角回路的综合;再将伪攻角回路作为广义被控对象，基于定量反馈理论，完成法向过载回路设计。

3.1 伪攻角回路参数空间方法设计

给定理想的特征多项式:

设计反馈控制律K=［KαKr］，采用极点配置方法，可得

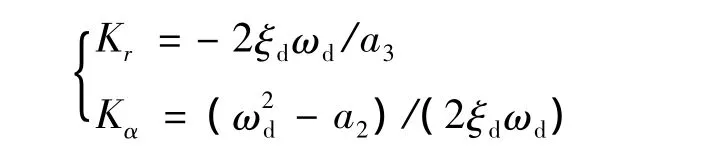
考虑摆动喷管控制导弹气动参数的不确定性及摆动喷管的控制误差，取4种模态寻找公共控制器K，给定理想的特征多项式参数 14≤ωd≤20，0.6≤ξd≤1.2，求出参数空间平面，如图4所示。

图4 控制器参数空间Fig.4 Controller parameter space

依据参数空间的交集，取Kr= －0.25，Kα=11。对于气动参数及摆动喷管不同的组合偏差，由伪攻角回路的阶跃响应曲线可知，伪攻角回路稳定性良好，仅存在不同的稳态值。

3.2 基于定量反馈理论的法向过载回路设计

将伪攻角回路及过载与攻角的比例系数作为广义被控对象，推导其传递函数为

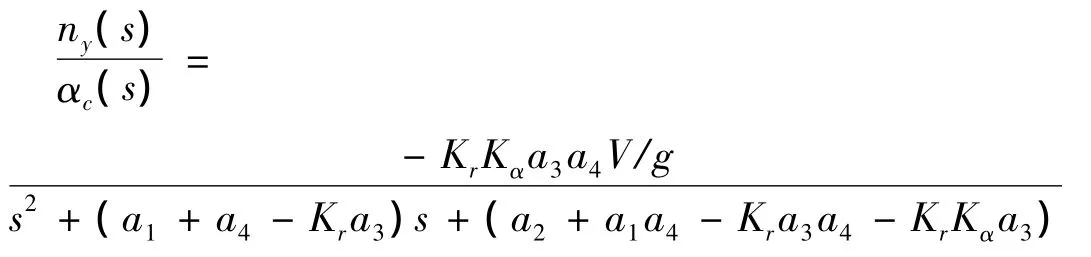
令

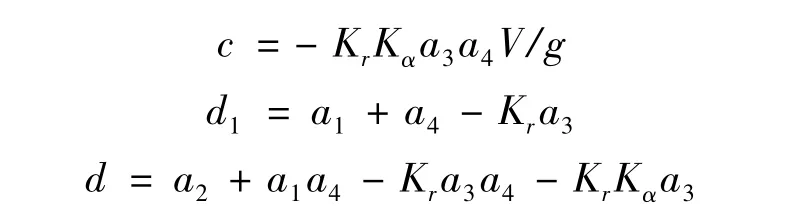
对于不同的偏差组合，广义被控对象传递函数系数的取值如表1所示。

法向过载飞行控制系统的指标要求为系统达到稳态80%的时间小于0.8 s;超调量小于10%。根据技术指标要求，取跟踪性能指标的上下界函数分别为

取Ws1=1.2，按照最小幅值裕度和最小相位裕度的计算式:

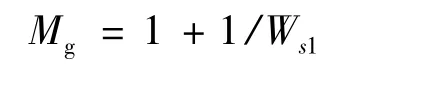
可知，Ws1所对应的最小幅值裕度为5.3 dB，最小相位裕度为50°。

表1 广义被控对象传递函数系数Table 1 Coefficients of generalized controlled object transfer function

通过回路成形，给出控制器及前置滤波器分别为

图5为俯仰通道法向过载控制系统阶跃响应仿真结果曲线。由图5可知，对于不同的偏差组合，法向过载控制系统上升时间为0.36～0.8 s，超调量小于5%。

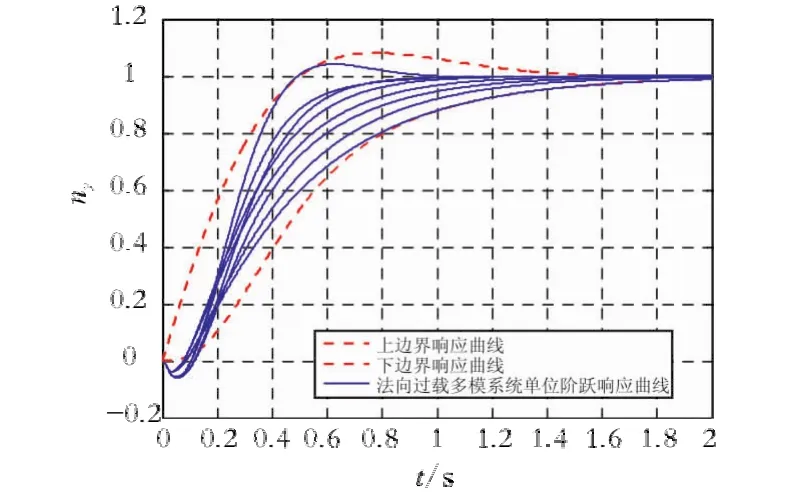
图5 法向过载回路阶跃响应曲线Fig.5 Step response curves of the normal overload control system

4 结论

(1)采用多模方法，通过区域极点配置，可解决伪攻角回路存在参数不确定性及执行机构控制误差时多模系统公共控制器的求解问题。

(2)基于定量反馈理论设计的法向过载回路控制器和前置滤波器，可使得法向过载回路在参数偏差条件下满足技术指标要求。

(3)本文方法解决了摆动喷管控制导弹给定工作点的鲁棒飞行控制系统设计，可将该方法与预定增益控制理论相结合，完成全空域的鲁棒飞行控制系统综合。

［1］张晓峰，祝小平，杨军.摆动喷管控制导弹回路成形自动驾驶仪设计［J］.飞行力学，2010，28(6):60-63.

［2］Reynolds O R，Pachter M，Houpis C H.Full envelope flight control system design using quantitative feedback theory［J］.J.Guidance，Control and Dynamics，1996，19(1):23-29.

［3］Isaae Horowitz.Application of quantitative feedbaek theory(QFT)to flight control problems［J］.IEEE，1990:2593-2598.

［4］郑勇斌，林丽.采用摆动喷管推力矢量控制弹性弹体数学模型建立［J］.现代防御技术，2007，35(1):41-44.

［5］郑勇斌.摆动喷管控制精度相关问题讨论［J］.现代防御技术，2007，35(3):54-57.

［6］朱学平，杨军.基于定量反馈理论的无人机鲁棒飞行控制系统设计［J］.西北工业大学学报，2012，30(1):56-60.