基于高阶矩法的导弹吊挂与滑轨接触可靠性分析①

何新党，苟文选，刘永寿，高宗战

(西北工业大学力学与土木建筑学院，飞行器可靠性工程研究所，西安 710129)

0 引言

吊挂是导弹导轨式发射的重要装置，当飞机带弹飞行时，吊挂起到连接导弹与飞机机身的作用。吊挂在工作时与滑轨接触，当受到重力作用发生变形后，往往伴随着局部高应力。因此，分析结构中的接触现象，了解结构的接触状态和应力状态，对结构的设计和故障诊断都有非常重要的意义。

结构可靠性分析可以量化参数不确定性对结构性能的影响，灵敏度分析可获得参数变化对结构失效概率及参数重要性程度的横向对比，因此近年来受到各国学者的广泛关注［1－4］。然而对于大量工程结构而言，目前的可靠性分析方法依然难以实施［5－6］。主要原因在于大多数工程结构的基本变量与结构应力响应之间没有解析的数学表达式，需要通过有限元仿真方法获得结构性能与参数之间的响应，其计算过程往往需要大量时间。因此对于这种隐式功能函数下的可靠性分析问题，传统的基于大量抽样的可靠性分析方法的计算量往往难以接受［7－11］。另外，目前绝大多数的工程结构都有较高的可靠性要求，其失效概率往往很小。对于小失效概率的结构而言，基于代理模型(如Kriging 法［12－13］，响应面法［14］)的近似解析可靠性分析方法往往难以保证分析的精度。因此，建立一种在工程上能够兼顾效率与精度的可靠性分析方法无疑是亟待解决的问题［15］。

本文以某导弹吊挂结构为研究对象，开展了尺寸随机变量影响下的结构可靠性及参数灵敏度分析。首先借助有限元软件二次开发技术，建立了导弹与滑轨接触时非线性有限元分析的参数化模型，在静力学分析的基础上，将四阶矩方法引入导弹吊挂的可靠性分析，该方法可以充分利用变量分布各阶矩信息，在可靠性分析时抽样次数少，计算精度高，避免了改进一次二阶矩法需要求功能函数偏导数以及传统蒙特卡洛法及重要抽样法需要大量抽样等缺点。

1 吊挂和滑轨接触时的静力学分析

1.1 有限元模型

导弹吊挂结构的尺寸参数如图1所示。

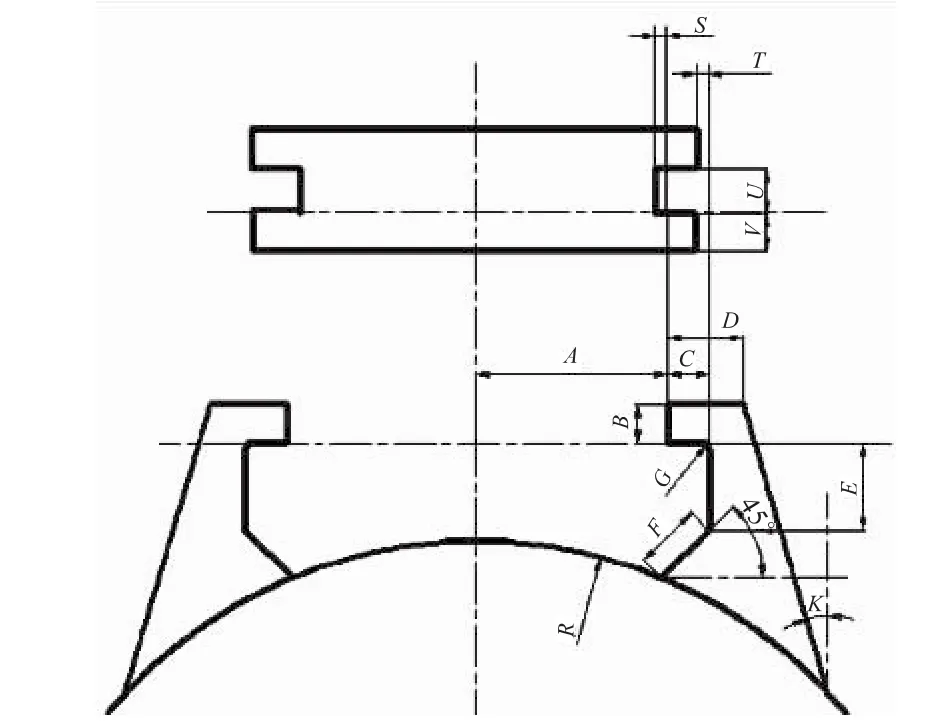
图1 导弹吊挂与滑轨二维装配图Fig.1 Assembly drawing of missile suspension and rail

模型由2部分组成，上侧为滑轨，下侧为导弹与吊挂的整体模型。2种结构的材料参数见表1。

在有限元软件中建立的导弹吊挂与滑轨的参数化有限元模型如图2所示。

表1 吊挂与滑轨的材料参数Table 1 Material property of suspension and rail

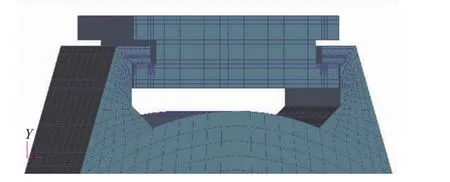
图2 导弹吊挂与滑轨有限元网格模型Fig.2 FEM of missile suspension and rail

1.2 静力学分析及强度校核

飞机在挂弹飞行时，导弹通过吊挂与飞机相连接，吊挂承担着导弹的重力作用，是吊挂受载的主要来源。因此在结构的强度校核时，本文主要考虑导弹重力作用。在有限元非线性接触性分析时，导弹与滑轨之间的接触定义为柔体-柔体接触。滑轨上端固定约束，导弹的重力载荷施加于导弹圆心处。通过非线性接触分析得到导弹吊挂与滑轨之间的应力云图如图3所示。

图3 导弹吊挂与滑轨应力云图Fig.3 Diagram of stress distribution on missile suspension and rail

分析得到滑轨的最大接触应力为468 MPa，吊挂的最大接触应力为462 MPa;吊挂材料的屈服极限为830 MPa，滑轨材料的屈服极限为860 MPa。为了保证给结构保留一定的安全裕度，选取安全系数ns=1.5校核吊挂结构，830/468=1.77，860/462=1.86 均大于安全系数ns。因此，结构满足安全系数为1.5时的设计要求。

2 可靠性分析

考虑到关键尺寸分散性对结构强度的影响，建立吊挂结构强度失效功能函数，编写相应的计算机程序，采用四阶矩法对导弹吊挂结构进行可靠性和灵敏度分析。

2.1 可靠性分析模型

通过静力学分析发现结构吊挂耳片与滑轨的接触区存在局部高应力，因此在进行可靠性分析时，选择图1中所示的4个关键尺寸参数A、B、C、D作为基本随机变量，其中A为吊挂的耳片内侧距中心线的距离，B为耳片的厚度，C为耳片内侧长度，D为耳片外侧长度。其具体分布参数如表2所示。

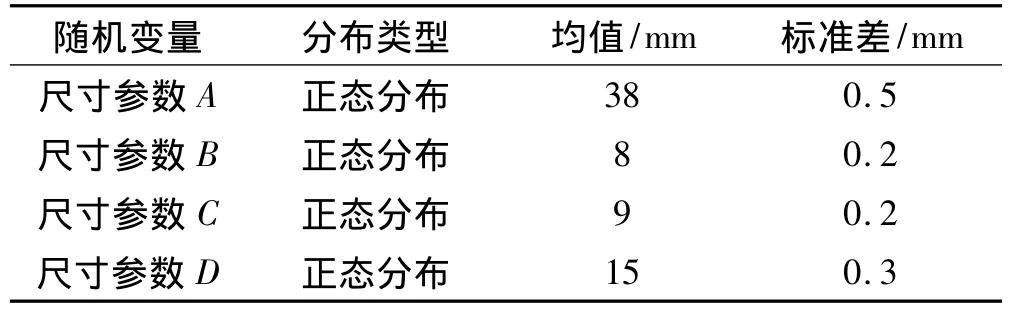
表2 随机变量及分布类型Table 2 Random variables and distribution characters

考虑到滑轨的最大应力远小于其屈服强度，因此只考虑吊挂的强度失效，其功能函数为

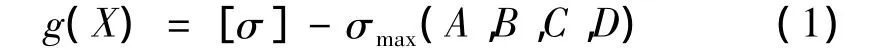
式中 g(X)均为基本变量X的隐式函数，需要调用有限元软件计算基本变量每次取值时对应的极限状态函数值;［σ］为结构的许用应力，当安全系数ns=1.5时，［σ］= σs/ns=830/1.5=553 MPa，其中 σs为屈服应力;σmax为通过有限元方法计算得到的结构最大Mises应力。

2.2 可靠性分析方法

本文采用四阶矩方法对导弹吊挂结构进行可靠性分析［16］，该方法以概率矩为基础，直接利用功能函数在一些特征点处的函数值来近似计算功能函数的低阶矩(主要是一阶至四阶矩)，然后由功能函数的各阶矩来近似失效概率。与其他可靠性分析方法相比，该方法避免了改进一次二阶矩法求功能函数的偏导函数以及数值模拟法大量抽样等问题，在分析时求解功能函数值的次数仅为3n。因此，特别适用于变量个数不多的复杂工程结构的可靠性分析。

结构的失效概率Pf可表示为

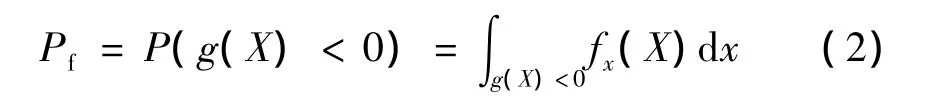
式中 fx(X)为功能函数g(X)的联合概率密度函数。

设 X={x1，x2，…，xn}为联合概率密度函数为fx(X)的随机变量，则结构响应功能函数g=g(X)=g(x1，x2，…，xn)的各阶概率矩可由式(3)～ 式(6)计算得到:

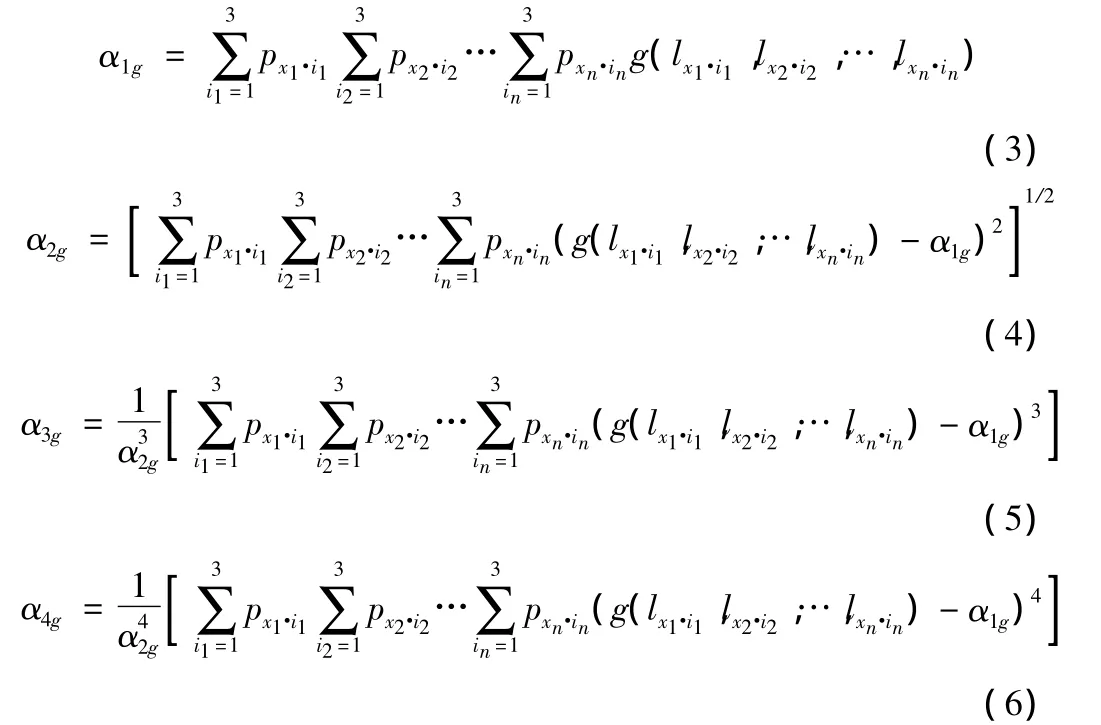
式中 α1g、α2g、α3g、α4g分别为功能函数 g=g(X)=g(x1，x2…，xn)的均值、标准差、偏度和峰度。

对于第k个变量xk的参数pxk·ik和lxk·ik，可以由xk的均值 α1xk、标准差 α2xk、偏度 α3xk和峰度 α4xk按式(7)～式(12)类似给出。

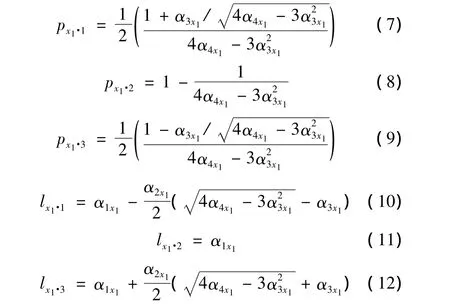
功能函数的概率矩给出了功能函数的部分统计信息，它与功能函数的概率密度函数是紧密相关的，获得了功能函数g(x)的概率矩，那么就可非常容易得到失效概率了。在考虑功能函数前四阶矩来近似失效概率的方法为四阶矩法。基于四阶矩的可靠度指标为

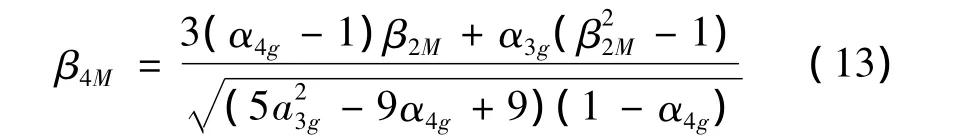
式中 β2M为功能函数前两阶矩的可靠度指标，可近似为 β2M= α1g/α2g。

相应地考虑前四阶矩的失效概率为

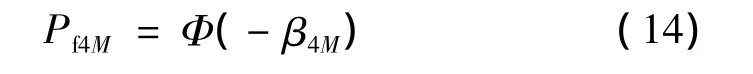
3 参数灵敏度分析

可靠性参数灵敏度分析的目的是研究可靠性模型中各基本随机变量或其参数变化对失效概率或可靠度指标的影响规律，从而识别影响结构可靠性的关键参数。可靠性灵敏度定义为失效概率Pf对基本变量X={x1，x2，…，xn}的分布参数的偏导数，这里 i=1，2，…，n，k=1，2，…，mi。其中 mi为第 i个变量 xi的分布参数的总个数。由失效概率Pf与可靠度指标的关系以及可靠度指标与极限状态函数各阶矩的关系，可以采用函数求导法推出Pf对基本变量分布参数的灵敏度计算式:

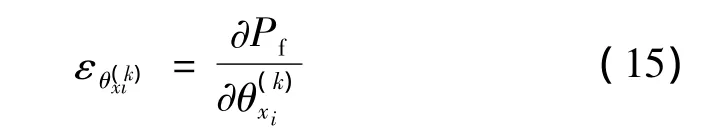
均值灵敏度反映了变量均值大小对可靠度的影响程度［7－8］。其相应的计算式:

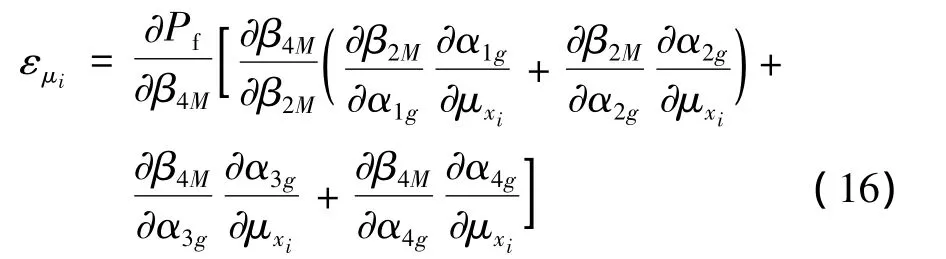
标准差灵敏度反映了变量参数波动性对可靠度的影响，其相应的计算式:

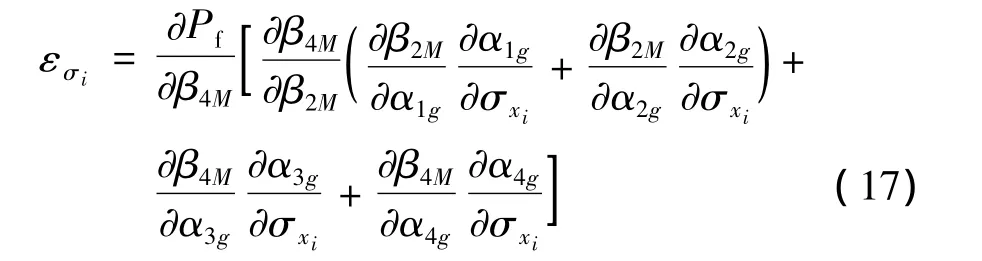
其中

4 分析结果及讨论

4.1 可靠性及灵敏度分析结果

由于功能函数中只有4个基本变量，四阶矩法只需调用81次就可获得功能函数的均值、标准差、偏度和峰度等，其中4个基本变量81次抽样过程曲线如图4(a)～(d)所示。吊挂局部最大应力抽样结果如图5所示。

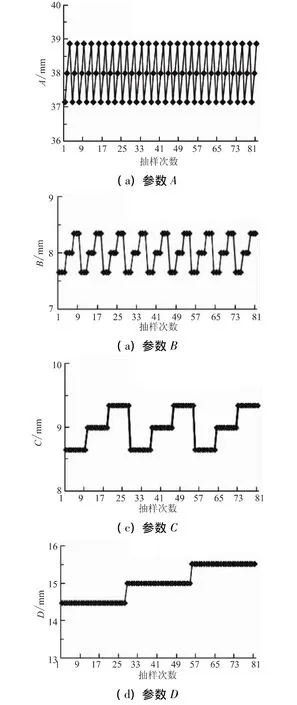
图4 各参数抽样结果Fig.4 Simple results of parameters

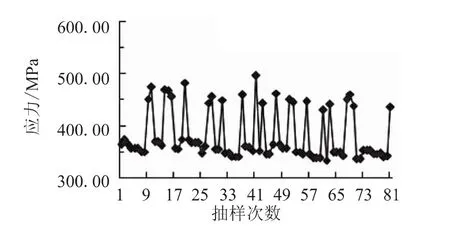
图5 吊挂局部最大应力抽样结果Fig.5 Simple results of stress

分析最终得到功能函数的前四阶矩为 α1g=259.162，α2g=35.944，α3g= －2.042，α4g=8.704，代入式(12)可得可靠度指标为β4M=3.235，失效概率Pf4M=0.000 607。

将功能函数的各阶矩对基本变量分布参数的偏导数代入式(16)、式(17)，可得到可靠性灵敏度，如表3所示。均值及标准差灵敏度分析结果(直方图)见图6。

表3 四阶矩法对参数灵敏度分析结果Table 3 Results of basic parameters sensitivity analysis by fourth moment method

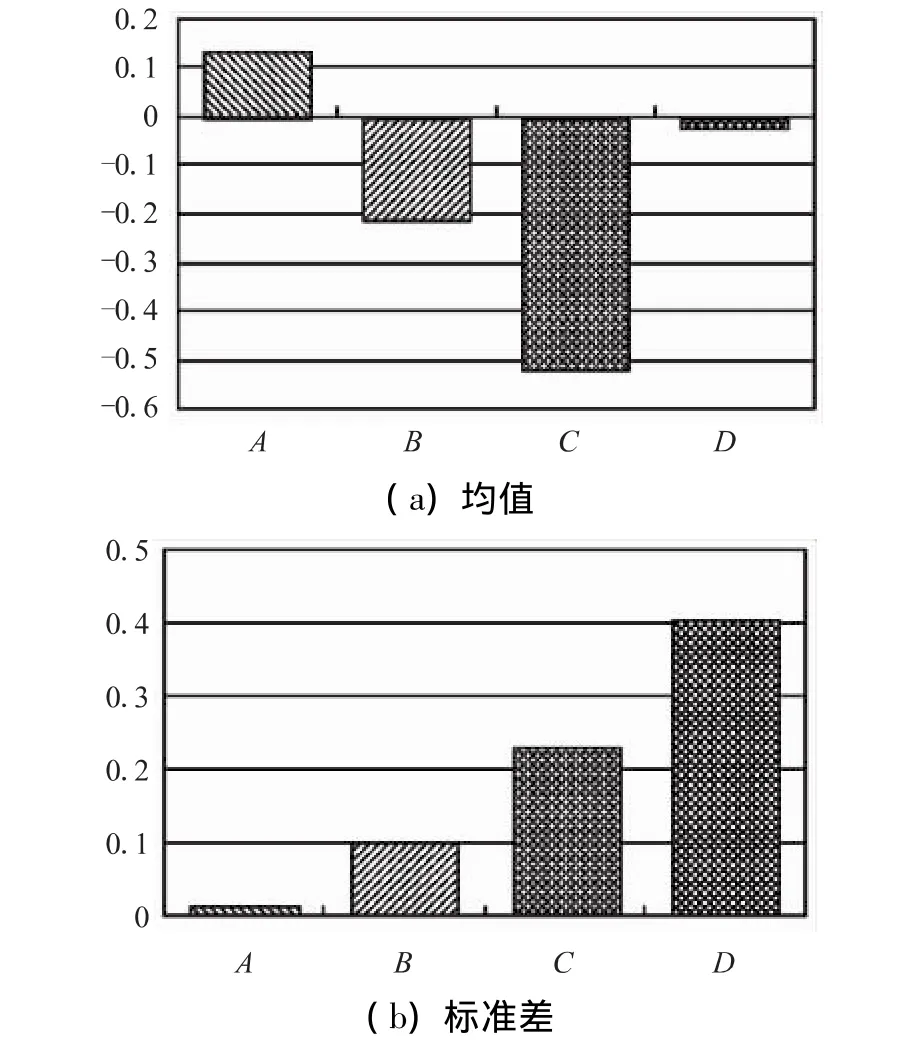
图6 均值及标准差灵敏度分析结果直方图Fig.6 Sensitivity analysis results diagram of mean value and standard deviation

通过均值灵敏度分析结果可知，耳片内侧长度尺寸C是影响导弹吊挂结构强度的最主要因素，其次是耳片厚度B。因此在结构设计时可着重优化该尺寸变量来提高结构强度性能。通过标准差灵敏度分析，可以看到耳片外侧长度D的分散性对结构性能稳定性的影响较大，其次是耳片内侧长度C。因此应该适当减小尺寸D和C的设计公差，并严格控制其加工误差，从而提高结构的性能的稳定性。

4.2 其他可靠性方法比较

为了验证本文采用的可靠性分析方法在计算效率与精度上的优势，将四阶矩法(Fourth-Moment Method，FMM)的分析结果与蒙特卡洛法(Monte-Carlo，MC)、重要抽样法(Importance Sampling Method，ISM)、改进一次二阶矩法(Advanced First Order and Second Moment，AFOSM)、加权二次响应面法(Response Surface Method，RSM)进行了比较，各方法分析结果见表4。

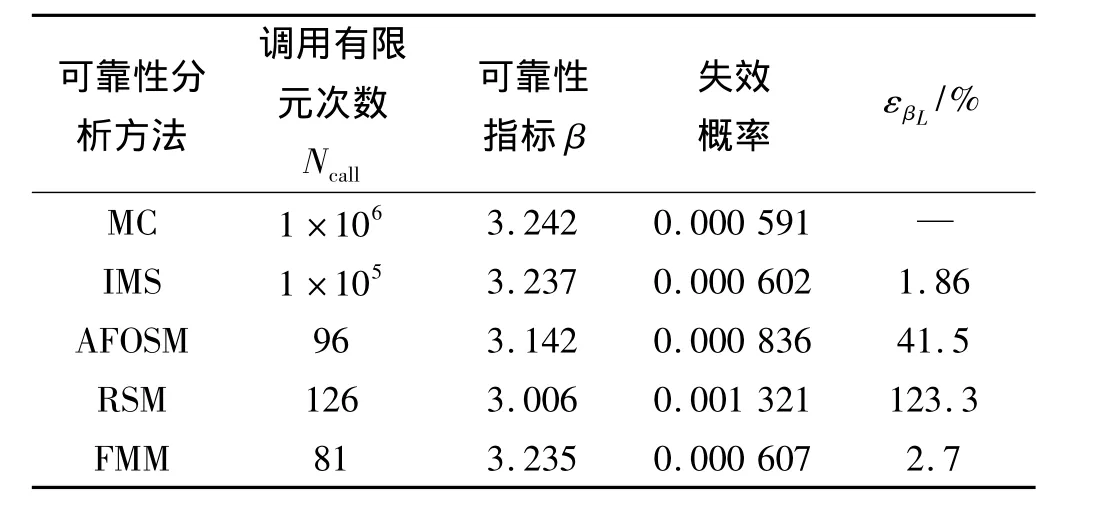
表4 多种可靠性方法分析结果Table 4 Results of multifold reliability analysis methods

其中蒙特卡洛法在样本充足的情况下往往被认为是最为精确的方法，因此本文以该方法作为验证其他方法分析精度的标准。从计算误差来看，重要抽样法是其他4种方法中计算误差最小的方法，但其计算成本依然很高。本文采用的四阶矩方法在极大减小计算成本的前提下，保证了较高的分析精度，计算误差仅为2.7%，因此可认为是处理复杂工程问题较为理想的方法。

5 结论

(1)本文所采用的四阶矩法在已知结构的变量类型和分布参数情况下，仅通过调用有限元软件81次抽样就可以快速求解出结构失效的概率及变量灵敏度，在极大减小计算成本的前提下，保证了较高的分析精度，是处理复杂工程问题较为理想的方法。

(2)接触可靠性分析结果表明，按照传统安全系数法进行强度校核合格的导弹吊挂结构，当考虑结构的尺寸分散性时，其强度失效概率为0.000 607，难以满足武器装备高可靠性的要求，因此在结构设计时需要考虑尺寸分散对结构性能的影响。

(3)均值灵敏度分析表明，耳片内侧长度尺寸C和耳片厚度B是影响导弹吊挂结构强度的最主要因素，因此，在设计时应考虑适当增加其尺寸数值，以提高结构的强度可靠性。标准差灵敏度表明耳片外侧长度D的分散性对结构性能稳定性的影响较大，其次是耳片内侧长度C，因此，应该适当减小该尺寸设计公差，并严格控制加工误差，从而提高结构的性能的稳定性。

(4)与其他可靠性分析方法的计算结果比较，本文方法克服了传统可靠性分析方法需要大量抽样的缺点，能在较短时间里得出满足工程精度的结果，在解决复杂工程问题时有其独特的优越性，具有很好的工程应用前景。

［1］王光远.论不确定性结构力学的进展［J］.力学进展，2002，32(2):205-211.

［2］高宗战，刘志群，姜志峰，等.飞机翼梁结构强度可靠性灵敏度分析［J］.机械工程学报，2010，46(14):194-198.

［3］Ditlevsen O，Madsen H O.Structural reliability methods［M］.Coastal:Maritime and Structural Engineering，2007.

［4］Ryoichi Chiba.Reliability analysis of forming limits of anisotropic metal sheets with uncertain material properties［J］.Computational Materials Science，2013(69):113-120.

［5］Sundar V S，Manohar C S.Updating reliability models of statically loaded instrumented structures［J］.Structural Safety，2013(40):21-30.

［6］Deng Jian.Structural reliability analysis for implicit performance function using radial basis function network［J］.International Journal of Solids and Structures，2006(43):3255-3291.

［7］Huang Bei-qing，Du Xiao-ping.Probabilistic uncertainty analysis by mean-value first order Saddlepoint approximation［J］.Reliability Engineering and System Safety，2008(93):325-336.

［8］Hans Janssen.Monte-Carlo based uncertainty analysis:Sampling efficiency and sampling convergence［J］.Reliability Engineering and System Safety，2013(109):123-132.

［9］Cardoso J B，de Almeida J R，Diasa J M，et al.Structural reliability analysis using Monte Carlo simulation and neural networks［J］.Advances in Engineering Software，2008(39):505-513.

［10］Pilger G G，Costa J F，Koppe J.The benefits of Latin hypercube samplingin sequentialsimulation algorithmsfor geostatistical applications［J］.Applied Earth Science，2008，117:160-74.

［11］Echard B，Gayton N，Lemaire M，et al.A combined importance sampling and kriging reliability method for small failure probabilities with time-demanding numerical models［J］.Reliability Engineering and System Safety，2013(111):232-240.

［12］Echard B，Gayton N，Lemaire M.AK-MCS:an active learning reliability method combining Kriging and Monte Carlo simulation［J］.Structural Safety，2011，33(2):145-54.

［13］BarronJ Bichon，JohnM McFarland，Sankaran Mahadevan.Efficient surrogate models for reliability analysis of systems with multiple failure modes［J］.Reliability Engineering and System Safety，2011(96):1386-1395.

［14］Jorge E Hurtado.An examination of methods for approximating implicit limit state functions from the viewpoint of statistical learning theory［J］.Structural Safety，2004(26):271-293.

［15］Bourinet J M，Deheeger F，Lemaire M.Assessing small failure probabilities by combined subset simulation and support vector machines［J］.Structural Safety，2011，33(6):343-53.

［16］Lv Zhen-zhou，Song Jun，Song Shu-fang.Reliability sensitivity by method of moments［J］.Applied Mathematical Modeling，2010(34):2860-2871.