耳片接头系数的研究
2022-04-08梁荣娜秦建兵
梁荣娜 秦建兵
(中航西安飞机工业集团股份有限公司设计院,陕西 西安 710089)
0 引言
在航空工业中,耳片是一种必不可少的接头形式,多用于连接飞行器的关键结构。从受力角度来说,耳片主要分单剪耳片、双剪耳片及多剪耳片。从结构形式来说,可以分为直耳片和斜耳片。从受载形式来说,耳片受轴向拉伸载荷、斜向拉伸载荷和压缩载荷。耳片孔周围的应力状态十分复杂,主要承受周期载荷,且载荷全部来自销子。在耳片和销子之间引起的高应力集中和微动磨蚀是产生裂纹的主要原因,在周期载荷下,裂纹也会扩展。
当销钉与耳片连接的结构中有衬套时,在连接面会产生3种非线性接触问题:1) 干涉配合的衬套与耳片接触分离。2) 销子与衬套间隙配合,销子受力时所形成的协调接触。3) 衬套和耳片在接触面上的相对滑移。N.Antoni通过平面接触模型研究了上述销钉耳片中的非线性接触问题,该模型中耳片弹簧刚度的分配参考了Winkler模型,耳片周围的应力分布也得到了大量文献的验证。研究结果指出,当发生接触分离时,耳片会出现软化现象,这是非线性接触退化所固有的现象,而且结构全局响应的变化主要发生在分离的起始阶段。如果在初始阶段有间隙,那么销子一旦受力就会加剧了模型的整体响应,这是非线性接触增加的结果。当衬套和耳片之间存在库伦摩擦力时,在单调载荷下,力-位移之间的关系开始弱化,滑移起始阶段结构的全局响应变化最大。J. VOGWELL等人开展了耳片的静力、疲劳和断裂分析,由分析结果可知,耳片的受力形式对剪应力有较大的影响。与间隙配合相比,过盈配合可以降低峰值应力的大小,耳片在纵向受力下的峰值应力比在垂向受力下的峰值应力大。Michael A.Brown等人研究了7075-7651铝合金耳片与钢衬套在不同过盈量配合下的疲劳性能,试验结果显示,虽然3种过盈量不大且差别很小,但是呈现的S-N曲线明显不同,说明过盈量的微小变化对耳片寿命有较大的影响。
1 耳片接头系数
耳片头部处于拉伸、弯曲和剪切复合受力的状态下,当采用工程方法和软件有限元法计算耳片强度时,简化分析过程、合理考虑修正系数就非常重要,当耳片受轴向拉伸时,通常不考虑耳片的破坏形式,用沿孔中心横向截面上的平均应力来计算耳片强度,耳片受斜向拉伸载荷,目前采用轴向拉伸载荷计算是偏危险的,当耳片载荷为斜拉伸载荷时,孔两侧的刚度开始变化(逐渐不相等),刚度大的一侧受力较大,因此,在斜载荷作用下,耳片弯曲变形,耳片沿孔厚度方向的载荷分配不均匀,导致耳片承载能力变弱,耳片在压缩载荷的作用下,先将压缩载荷分解为轴向载荷和切向载荷,然后将切向载荷等效,再按照斜拉伸载荷分析计算。上述各种分析方法会直接影响耳片疲劳寿命的分散性,尤其是在损伤容限分析的过程中,软件使用的模型简单,为了保证模型的有效性,该文对斜载系数K、弯曲系数K以及间隙系数K进行研究。
2 斜载系数Kθ
耳片结构主要承受轴向、斜向以及垂向外载荷,载荷如图1所示。将外载荷分解为轴向P和垂向P;如果载荷与耳片中心孔夹角为,则可将载荷分解为P和P。承受斜载耳片大量存在于实际工程中,例如飞机结构操纵摇臂、部件连接件和作动筒等耳片结构,其载荷形式和耳片轴线成一定的角度,静强度分析时各种加载角度下的许用应力计算方法、计算公式是基于大量试验数据拟合出来的,用于初步设计结构和静强度校核时确定许用载荷。耳片结构复杂,但是对损伤容限分析、计算工作应力并没有参考价值,且NASGRO的CC03模型没有加载角度这个输入项,因此引入斜载系数K,基于有限元分析,查看不同角度斜向加载时耳片孔边垂直裂纹面的最大主应力,并以0°轴向加载时的应力值为基准进行无量纲化,最终得到系数曲线。

图1 耳片结构受载形式示意图
2.1 有限元模型
采用MSC/Patran建立有限元模型,耳片销钉尺寸为23.8mm,耳片中心孔距离约束端236mm,耳片宽为54mm,厚度为25.23mm。因为耳片孔边有明显的应力集中,所以对孔周围的网格进行细化,而在离孔边较远的部位应力分布会比较均匀(不需要关注),因此远端粗化网格,其目的是减少计算量,在连接过程中,销钉的刚度大于耳片刚度,为了在就算过程中防止销钉的网格嵌入耳片中,需要保证销钉的网格比耳片的网格粗,且销钉的网格要尽量保持轴对称的形式。
耳片和销钉材料选用常见的线弹性材料,弹性模量和泊松比参数见表1。

表1 斜载系数计算模型材料参数
销钉中心处施加31 314 N的集中载荷,加载方向沿轴向变化,耳片根部全约束,销钉与耳片之间采用硬接触,不考虑摩擦。
2.2 计算结果
以耳片角度和集中加载角度双参数为变量,计算耳片角度分别为0°、20°、40°和60°时集中力加载角度以15°为步长,分别从0°变化到90°的孔边最大主应力,各变量中耳片孔边的最大主应力数值见表2。
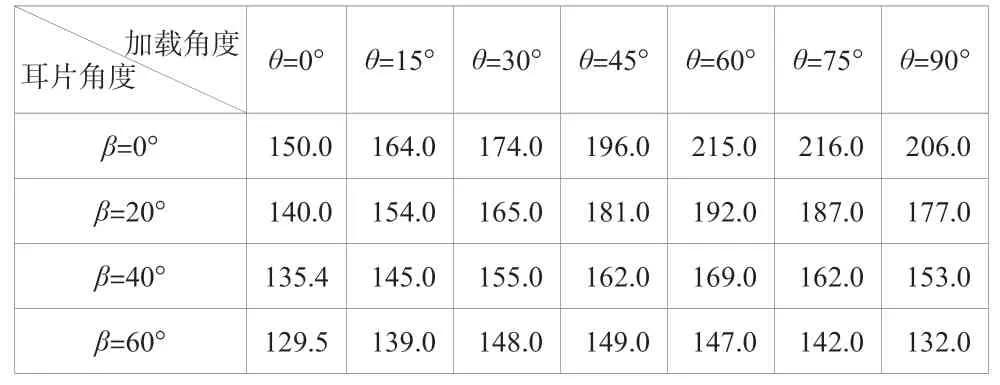
表2 不同加载角度下耳片孔边最大主应力(单位:MPa)
将表2中的应力值与=0°、=0°时的应力值进行比较可以得到无量纲化后的斜载系数曲线,如图2所示。

图2 耳片斜载系数KB
由比较结果可知,当耳片角度分别为0°、20°、40°和60°时,孔边最大主应力逐渐增加且增加幅度基本一样;当耳片角度分别为0°、20°、40°和60°时,耳片孔边最大主应力随加载角度的变化逐渐增加,在加载角度为45°~75°时达到最大值,然后逐渐回落, 加载角度为90°时仍大于0°时的最大主应力。当分析计算时,可根据耳片角度和载荷与耳片轴线之间的夹角选用适用的系数进行修正。
3 间隙系数KG
一般情况下,耳片与螺栓或销钉之间属于小间隙配合。如果耳片未安装衬套,那么钉杆与孔壁的挤压面积将会比紧配合时小,挤压力会明显高于理论值,耳片在载荷的作用下,U型接头两端耳片均承担/2的载荷,应力严重部位会从过耳片中心点与轴向载荷的交点处逐渐向载荷垂线点处过渡。由分析计算的结果可知,耳片中心点与轴向载荷交点处应力值最大,以该点为中心向两边过渡,应力逐渐减小,这种现象也可以通过销钉与耳片接触形式说明,因此引入间隙系数K来消除这一影响。对有衬套的耳片结构来说,间隙系数同样适用。
3.1 无衬套模型
模型取2.1节中的直耳片模型,载荷及边界条件也一样,销钉的材料用钢,见表3(存在 0.1 mm 的间隙配合)。

表3 间隙系数无衬套计算模型材料参数
配合无间隙时耳片孔边危险部位的最大主应力为150MPa,销钉直径缩小0.1mm之后耳片孔边最大主应力增大到了180MPa,因此对无安装衬套的耳片来说,当配合间隙小于或等于0.1mm时,可以取间隙系数=180/150=1.2,对配合间隙大于0.1mm的少数耳片与销钉配合结构也可通过该方法计算间隙系数计算。
3.2 含衬套模型
《飞机设计手册(第10册 结构设计)》中指出衬套和耳片孔之间的配合推荐干涉配合。耳片模型同2.1节,销钉直径缩小至19 mm,衬套厚度为2.4 mm。模型分2个步骤求解:1) 安装衬套,增大衬套外径(增加0.2%,为衬套直径),从而模拟衬套与耳片之间0.2%的干涉量。2) 施加钉载。
由计算结果可知,2步求解之后耳片孔周围最大为192 MPa。该单元在第一步安装衬套后的孔边最大主应力为43.8 MPa。虽然最后的应力数值大于无衬套模型的解,但对损伤容限分析来说,钉载造成的幅值为192-43.8=148.2 MPa,比无衬套紧配合模型的幅值150 MPa还要小,因此对有安装衬套的耳片结构来说,可以按无衬套情况乘以1.2倍间隙系数来计算工作应力,结果是保守的。
4 弯曲系数KB
由于在外载的作用下销钉/螺栓肯定会发生弯曲,因此挤压应力在耳片孔内壁上的分布十分复杂(不是均匀分布的)。在损伤容限分析时为保守计算,应该选取沿厚度方向的峰值应力作为工作应力,因此引入弯曲系数来考虑耳片结构的三维效应。计算三维叉耳模型的最大主应力,然后以二维模型的应力值为基准无量纲化,就可以得到弯曲系数,校核中间耳片时不用考虑该系数。
4.1 有限元模型
有限元模型将2.1节中的2D模型改为3D模型,采用Solid单元,钉孔直径还是23.8 mm,如图3所示。图3中没有显示中间耳片。中间耳片宽度为54 mm,厚度为25.23 mm。侧耳片宽度为54 mm,厚度可以分为2 mm、4 mm、8 mm、16 mm、21 mm以及26 mm,考虑0.1 mm的配合间隙。

图3 计算弯曲系数的有限元模型
此外,将销钉中心处的集中力改为对中间耳片远处自由端施加拉应力,应力为45.89 MPa。
4.2 计算结果
耳孔内壁应力数值见表4,将表4的应力值除以第三节考虑配合间隙模型中侧耳片的最大主应力180MPa,得到无量纲化以后的弯曲系数,见表4。

表4 侧耳片孔内壁最大主应力(单位:MPa)
将表4中的应力值除以第三节考虑配合间隙模型中侧耳片的最大主应力180 MPa,得到无量纲化以后的弯曲系数曲线,如图4所示。由分析计算结果可知,在耳片孔直径不变的情况下,随着耳片厚度的增加,耳片内壁的最大主应力也逐渐增大,弯曲系数也逐渐增大。

图4 耳片弯曲系数KB
5 结论
耳片连接件结构型式很简单,其优缺点也很明显。缺点是耳孔周围的应力状态复杂,应力集中系数相对较高。优点是安装和拆卸相对容易,2个连接部分之间可以旋转。在静载作用下,耳片的破坏形式随着耳片加载方向的改变而改变,在疲劳载荷作用下,耳片破坏位置及破坏形式还取决于最大应力集中的位置。破坏形式不一样,校核的方法也不一样。
该文研究了加载角度、配合方式以及应力分布对耳片受力的影响,引入了斜载系数、间隙系数以及弯曲系数,通过适当地放大载荷,简化了受力形式,考虑了耳孔局部非线性影响,结果显示该方法可以用来指导工程应用。
