柔性厚壁筒环向缠绕张力分析与设计①
2013-08-31刘成旭邢静忠
刘成旭,邢静忠,2,陈 利,杨 涛
(1.天津工业大学 机械工程学院,天津 300387;2.天津工业大学现代机电装备技术天津市重点实验室,天津 300387;3.天津工业大学复合材料研究所,天津 300387)
0 引言
在造纸、包装和轧钢等行业中,需要对带材进行卷绕(收卷)成形,以缩小贮存空间,或方便运输。在宽带卷绕过程中,恒张力卷绕经常导致带材皱折和厚度不均,这是由于外缠绕层张力对内层产生了放松效应。对于印刷行业,印刷机工作(开卷)时,会出现走纸不稳、印品折皱、重影,甚至发生纸张断裂或堵塞等问题,这是由于纸带张力不均匀引起的。因此,需分析研究初始缠绕张力与剩余缠绕张力之间的关系。如何设计初始缠绕张力,以达到缠绕后均匀的剩余张力,是解决这些问题的关键。目前,针对宽带缠绕张力的诸多研究,主要围绕如何确定初始缠绕张力与剩余张力之间的关系。杨娅君等讨论了恒张力卷绕和锥度张力卷绕下卷筒内的张力分布,导出不起皱折的必要条件,给出在等张力和等径向应变分布条件下卷绕张力的计算公式[1]。吴德会等介绍了玻璃布包装过程中收卷张力控制系统的工作原理,并针对包装收卷过程中易产生折皱的问题,分析了包装收卷过程中的张力变化规律及其影响因素,给出了不同卷装条件下避免折皱的锥度系数的确定方法[2]。盛卫锋等基于动力学原理,分析了印刷机械中的张力控制问题[3]。
相比宽带缠绕,纤维增强复合材料对缠绕张力的要求更高。尤其在国防和航天等高尖端领域,施加预张力的纤维增强复合材料,可达到更高的纤维体积含量和更高的结构开裂强度。所以,预张力纤维缠绕技术被大量用于飞机、火箭、航天器和卫星等结构上[4]。工业上,以金属为芯模的复合材料容器大多应用张力缠绕技术提高容器的承压能力和纤维的利用率。但金属的弹性范围小,过高的纤维张力会导致内衬屈曲。所以,研究芯模的刚度和缠绕张力之间的关系具有非常重要的意义。依据纤维缠绕复合材料的基本原理[5]和理论[6],许多研究者已围绕复合材料容器强度分析[7]与设计[8]的研究得出了一些张力计算公式[9-10],并提出了具有金属内衬的纤维缠绕高压容器的设计方法[11-12]。研究发现,纤维张力放松量主要来源于芯模的径向变形,同时在外层缠绕张力引起的径向外压下,缠绕层产生的径向和环向收缩,使环向应力降低。文献[13]未考虑芯模变形影响,给出了刚性芯模上环向缠绕层张力分析的计算方法和缠绕张力设计方法。但针对柔性芯模,如何使剩余缠绕张力达到预定分布,仍没有很好地解决。
本文考虑芯模的变形影响,依据弹性力学厚壁筒理论,提出考虑芯模变形影响的剩余张力分析方法和缠绕张力设计方法。采用叠加原理,基于外层剩余张力导致内层张力的放松量导出缠绕后剩余张力与缠绕张力的微分方程;通过对给定缠绕张力确定剩余张力和给定要获得的剩余张力确定应施加的缠绕张力两类问题的研究,讨论芯模厚度对缠绕层剩余张力的影响。
1 芯模和缠绕层的应变和应力
将收卷辊简化为外半径为c的宽带环向缠绕在外半径为b内半径为a的柔性圆筒上,在最外层宽带上施加均匀环向外压p,如图1所示。
1.1 平衡方程
在缠绕张力引起的外压作用下,芯模外表面和最内层纤维之间密切接触,接触界面上的径向位移与径向应力连续。设带有上标“(1)”和“(2)”的符号分别代表关于芯模与缠绕层变量。下标“r”、“θ”和“z”的变量分别表示沿径向、周向和轴向的物理量。缠绕层和芯模的微元体均满足平衡方程:
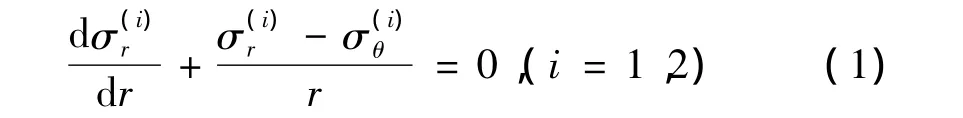

图1 模型的横截面Fig.1 Cross section of model
1.2 几何方程和物理方程
对于小变形情况,定义位移u和应变ε满足如下几何关系:

假定芯模与缠绕层近似满足各向同性三维本构关系,则芯模和缠绕层的应力与应变关系可表示为
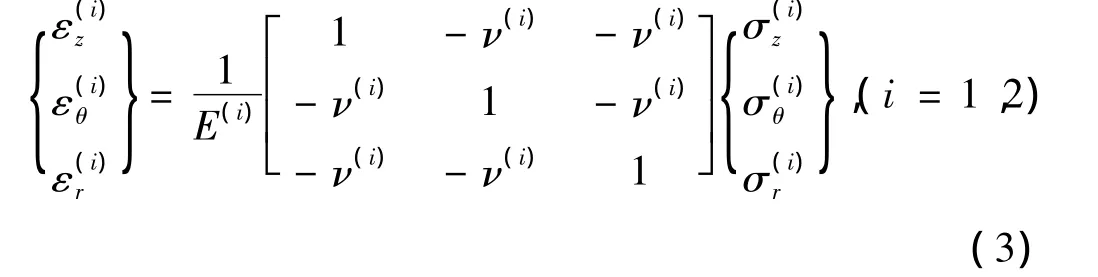
1.3 径向位移和应力分量
结合式(2)和式(3)关系,式(1)可化简为
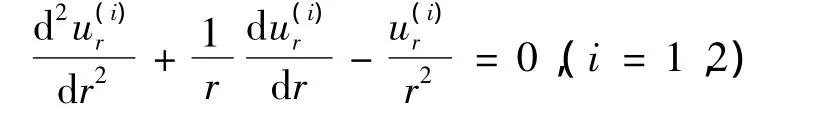
其通解为

积分常数A(i)和B(i)由芯模和缠绕层内外侧的边界条件确定。将式(4)代入式(1),整理可得芯模与缠绕层的应力表达式:

在平面应力情况下,只需要将上式中的弹性模量E(i)替换为 E(i)(1+2ν(i))/(1+ ν(i))2,泊松比 ν(i)替换为ν(i)/(1+ν(i))即可。其中,拉密常数:

1.4 芯模径向刚度
引入芯模径向的广义刚度:

由芯模内外壁的边界条件:

对于两端固定,轴向应变为零的情况,求得

1.5 缠绕层边界条件及其应力
缠绕层内侧与芯模接触面上的径向变形与径向应力成线性反比关系,则缠绕层内外侧的边界条件可表示为
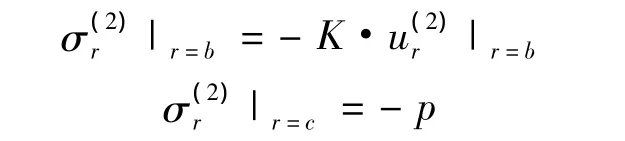
由此求得积分常数A(2)、B(2),将其及广义刚度K代入式(5),可求得缠绕层的环向应力和径向应力:
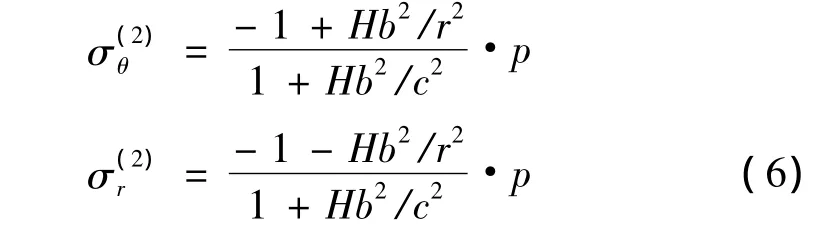
其中,引入影响因数

2 缠绕张力和剩余张力分析
由式(6)可知,外压p引起的缠绕层应力和应变不仅与缠绕层和芯模的材料参数有关,还与缠绕层几何尺寸有关。随着缠绕层数的增加,外层缠绕张力引起的外压增大,使内缠绕层的剩余张力不断减小。定义很薄的单位宽度的宽带缠绕在柔性芯模上,其初始缠绕张力分布为Tw(r)。这样的初始缠绕张力Tw(r)减去外层张力引起的张力放松量ΔT,即为该层的剩余缠绕张力T(r)。外半径为c的所有缠绕层上的总张力T(c)对该缠绕层内表面产生径向应力p=T(c)/c。

其中,δ是缠绕带的壁厚,此时半径c位置的环向应力下降量为
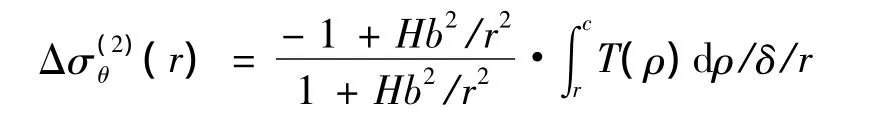
引入变换x=r/b和m=c/b,张力下降量可表示为

为了实现缠绕后的剩余张力达到指定的分布,需要利用式(7)计算出张力放松量,并与该层的初始缠绕张力叠加后等于指定的剩余张力,即

3 由初始缠绕张力确定剩余张力分布
根据给定的初始缠绕张力Tw(x)分布,确定缠绕后的剩余张力T(x)分布。最外层x=m处,有Tw(m)=T(m)。可将式(8)转化为

针对不同的应用情况,下面分别讨论锥度,等张力和等力矩缠绕情况下的剩余张力分布。
3.1 锥度缠绕
设锥度缠绕张力Tw(x)=t(1-αx),t和α分别为初始缠绕张力值和锥度系数,由式(9)可得
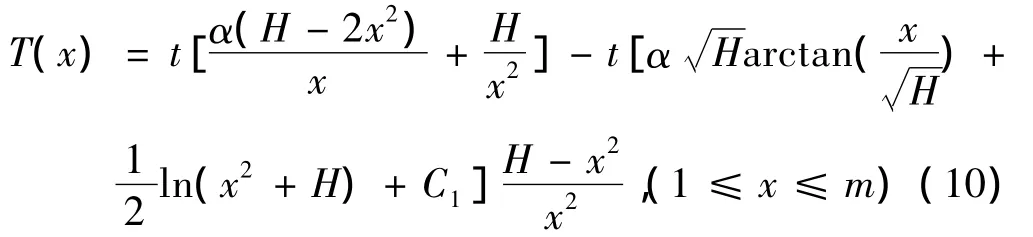
其中
采用SPSS 17.0软件对数据进行分析处理,计量资料以(均数±标准差)表示,采用t检验;计数资料以(n,%)表示,采用χ2检验,以P<0.05表示差异具有统计学意义。

3.2 等张力缠绕
设均匀缠绕张力Tw(x)=t,由式(9)可得

3.3 等力矩缠绕
设等力矩缠绕张力Tw(x)=t/x,由式(9)可得

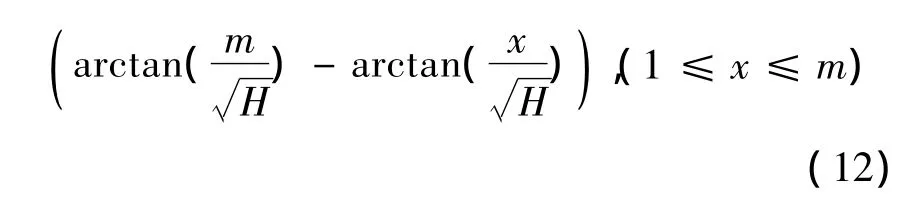
4 实现给定剩余张力分布的缠绕张力设计
对式(8)积分,给定缠绕后剩余张力分布,可求得初始缠绕张力的分布。给定均匀剩余缠绕张力T(x)=t,由式(8)可求得
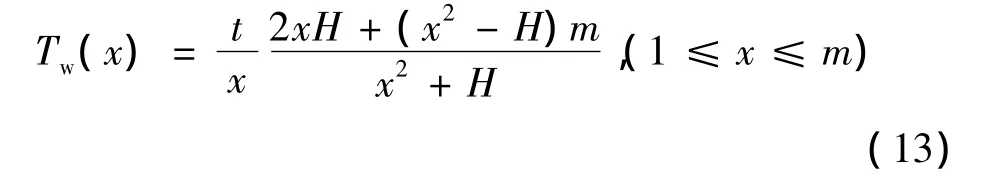
对其他分布的剩余张力,均可由式(8)积分获得缠绕张力设计方案。
5 数值算例和讨论
由式(10)~式(12)可知,决定剩余缠绕张力大小的因素有芯模和缠绕层的材料参数和几何参数。文献[13]提出缠绕层m、锥度系数α对剩余缠绕张力的影响。在此基础上,本文考虑芯模变形影响,讨论不同芯模内经α(单位:m)对剩余缠绕张力的影响。以薄板层为缠绕层,芯模材料采用钢。取弹性模量E=210 GPa,相对弹性模量 E21=1,泊松比 ν(1)= ν(2)=0.3。几何参数 b=0.5 m,c=1 m,m=2。
5.1 锥度缠绕后的剩余张力分布
图2所示为利用式(10)在不同内径芯模上取锥度系数α=0.3,锥度缠绕后的剩余张力分布。横坐标表示缠绕层所在的径向位置,纵坐标表示缠绕后的剩余张力与初始张力t的比值。剩余张力随着芯模内径a的减小而增大,即芯模壁厚越大,剩余张力越大;剩余张力是随缠绕层位置的增大而增大。

图2 锥度缠绕在不同a值时剩余张力沿径向的分布Fig.2 Residual tension distribution along radial direction by taper winding at different values of a
5.2 等张力缠绕后的剩余张力分布
图3所示为由式(11)给出不同内径芯模上等张力缠绕后的剩余张力分布。横坐标表示缠绕层所在的径向位置,纵坐标表示缠绕后的剩余张力与初始张力t的比值。剩余张力随着a的减小而增大,即芯模壁厚越大,剩余张力越大;剩余张力是随缠绕层位置的增大而增大。
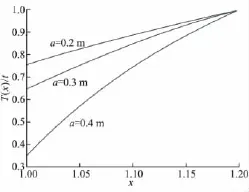
图3 等张力缠绕在不同a值时剩余张力沿径向的分布Fig.3 Residual tension distribution along radial direction by equal tension winding at different values of a
5.3 等力矩缠绕后的剩余张力分布
图4所示为由式(12)得到不同内径芯模上等力矩缠绕后的剩余张力分布。横坐标表示缠绕层所在的径向位置,纵坐标表示缠绕后的剩余张力与初始张力t的比值。剩余张力随着a的减小而增大,即芯模壁厚越大,剩余张力越大;剩余张力是随缠绕层位置的增大而增大。
5.4 实现均匀剩余张力的缠绕张力
假设缠绕后剩余张力为t,取缠绕层外径c=0.6 m,其他几何参数和材料参数与前面一致。图5所示为实现均匀剩余张力的缠绕张力分布。横坐标表示缠绕层所在的径向位置,纵坐标表示缠绕张力与剩余张力t的比值。由式(13)通过变化几何参数a改变芯模壁厚,进而得到相对缠绕张力随径向位置的变化曲线。
由图5可见,芯模的壁厚越大,缠绕张力越小。缠绕张力是随缠绕层位置的增大而减小。
5.5 与现有均匀剩余张力研究结果的比较
文献[14]利用有限元方法,计算了文献[15]给出的钢带缠绕实例。按该文的几何参数和材料常数,计算得到 H= -0.883 32,m=1.18,t=105 MPa。按式(13),得到最大内侧缠绕张力Tw(1)=410.1 MPa。考虑到本文分析为无限薄宽带连续缠绕,按照原文的缠绕带厚度修正m=1.18-0.007 5(缠绕带厚度δ与芯模外径b的比值),此时Tw(1)=397.4 MPa。按照每层缠绕带所处区间积分计算张力,获得354.2,288.9,244.1,211.5,186.7,167.3,151.7,138.9,128.3,119.3,111.6,105.0 MPa。对比表明,该结果介于文献[14]和[15]结果之间,并非常接近它们的平均值。而本文解析公式(13)简单实用。
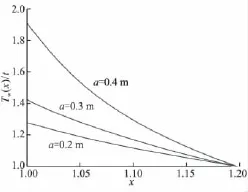
图5 在不同a值时实现均匀剩余张力的缠绕张力分布Fig.5 Winding tension leading to uniform residual tension distribution along radial direction at different values of a
6 结论
(1)在锥度缠绕、等张力缠绕和等力矩缠绕的情况下,剩余张力随径向位置的增大呈递增趋势,且随芯模壁厚的增大而增大。
(2)剩余张力分布和实现均匀剩余张力的缠绕张力分布可根据本文得出。
(3)本文计算方法考虑芯模变形影响,得出的缠绕张力和剩余张力计算公式能给出更贴合实际的结果。
[1]杨娅君,郭乙木.纺织物带材收卷后的应力分布[J].纺织学报,2003,24(6):564-566.
[2]吴德会,谭珍祥,杨华群.玻璃布包装中锥度收卷的内张力分布及其参数确定[J].包装工程,2005,26(6):8-11.
[3]盛卫锋,周一届,姜旻.印刷机械中的张力控制[J].包装工程,2001,22(2):4-7.
[4]谢霞,邱冠雄,姜亚明.纤维缠绕技术的发展及研究现状[J].天津工业大学学报,2004,23(6):19-22.
[5]冷兴武.纤维缠绕原理[M].山东科学出版社,1990.
[6]陈汝训.纤维缠绕壳体设计的网格分析方法[J].固体火箭技术,2003,26(1):30-32.
[7]陈汝训.具有衬里的纤维缠绕压力容器分析[J].固体火箭技术,1999,22(4):54-56.
[8]陈汝训.混杂纤维缠绕壳体设计[J].固体火箭技术,2001,24(3):10-13.
[9]丁保庚,杨福江.缠绕张力公式的研究[J].玻璃钢,2000(6):3-7.
[10]王树位.复合材料缠绕张力公式建立[C]//复合材料的现状与发展——第十一届全国复合材料学术会议论文集.2000:824-828.
[11]李卫东,王秉权.金属内衬纤维缠绕高压容器的设计[J].玻璃钢,1978,3:34-39.
[12]薛忠民.金属内衬纤维缠绕内压容器几个设计公式的探讨[J].玻璃钢/复合材料,1991(4):22-26.
[13]邢静忠,李家惠,陈利,等.刚性圆柱上环向缠绕张力的分析与设计[J].纺织学报,2011,32(8):122-127.
[14]任明法,郑长良,陈浩然.具有内衬的缠绕容器缠绕层等张力设计的迭代搜索[J].复合材料学报,2004,21(5):153-158.
[15]朱国辉,郑津洋.新型绕带式压力容器[M].北京:机械工业出版社,1995:85-90.
