HTPB推进剂粘聚断裂研究①

韩 波，鞠玉涛，周长省

(南京理工大学机械工程学院，南京 210094)

0 引言

固体推进剂药柱是固体火箭发动机的重要部件，药柱结构完整性分析是保证固体火箭发动机正常内弹道性能的必要条件。药柱表面微小裂纹的存在，对发动机能否正常工作有重大影响。因此，研究推进剂药柱表面微小裂纹的起裂、扩展规律具有十分重大现实意义。

目前，国内外针对含微小裂纹的固体火箭发动机药柱完整性分析，主要采用传统的断裂力学准则，如应力强度因子、能量释放率等。李九天等［1］使用三维奇异单元，计算了发动机药柱关键部位在内压载荷下的裂尖应力强度因子。Earnest［2］使用实验和数值仿真结合的方法，计算了推进剂的能量释放率，并用于发动机药柱的安全性分析。但由于实际裂纹扩展过程中材料产生了几何不连续，因此传统有限元方法不能准确模拟出裂纹的扩展过程。粘聚区模型(Cohesive Zone Model，简称 CZM)最早由 Barenblatt［3］和 Dugdale［4］提出用于研究脆性材料和塑性材料开裂过程。粘聚区模型为裂纹的起裂、扩展分析提供了一种强有力的方法。20世纪90年代，国外学者将粘聚区模型成功用于有限元数值仿真中，并取得了成功应用［5］。国内刘陆广等［6］使用粘聚区模型来仿真混凝土开裂过程。崔浩等［7］将粘聚区模型成功用于复合材料接头的失效分析中。粘聚区模型具有明确的物理意义和较高的计算精度。因此，可用于固体火箭发动机药柱裂纹开裂和扩展分析过程中。

1 粘聚区模型

HTPB推进剂是一种高固体含量的高聚物复合材料。其中，包含大量直径较大的高氯酸铵颗粒和直径较小的铝粉。在局部拉伸载荷作用下，HTPB推进剂会在裂尖首先产生颗粒脱湿，进而形成微孔洞，随着孔洞的不断扩大和合并，逐渐形成了宏观的裂纹。裂尖局部的颗粒脱湿和微孔洞称为裂尖损伤区，损伤区的损伤演化规律影响着裂纹的起裂和扩展过程。

图1为粘聚区单元模型示意图，(a)为常规有限元实体单元，单元之间共节点，无法直接模拟材料的宏观开裂过程;(b)为添加了粘结单元的有限元网格，实体单元之间通过粘结单元连接，粘结单元来模拟材料裂尖的损伤和演化直至宏观裂纹形成，裂纹的可能扩展路径为实体单元之间的界面。

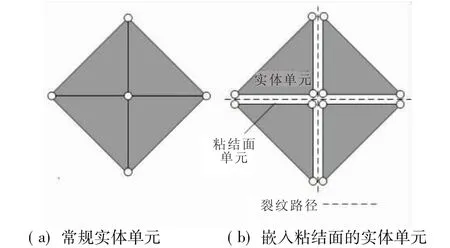
图1 粘聚区模型示意图Fig.1 Diagram of cohesive zone model

以平面Ⅰ-Ⅱ型复合裂纹为例，粘聚区单元有效位移和有效应力定义为

式中 δt和δn为裂尖粘结单元面上的切向和法向位移;σt和σn为裂尖的切向和法向力。

σe和δe之间的变化关系，即粘聚区的本构模型，它预示着材料裂尖的损伤和演化过程。图2为幂指数粘聚区本构的示意图。

图2中，横坐标代表材料裂尖损伤区变形量;纵坐标代表裂尖损伤应力。本构关系中，上升段是为了数值模拟的需要，代表着裂尖材料未损伤前的响应;下降段代表着材料的损伤软化形式。

式(2)为幂指数形式的粘聚区具体形式，可通过调节参数α来模拟不同形式的软化形式。

图2 幂指数粘聚区模型本构示意图Fig.2 Power law CZM constitution diagram

2 粘聚区本构的实验测定

粘聚区本构模型中包含3个重要参数:粘聚区断裂能、粘聚区断裂强度和粘聚区函数形式。国外有相关研究学者认为，粘聚区断裂能等于材料的临界扩展J积分［8］。因此，本文使用推进剂的临界扩展J积分作为粘聚区断裂能。Begley和Landes［9］提出了多试样法，通过一组初始裂纹长度相近的试件来测量材料的J积分。

多试样法需多个试样进行测量，实验量较大，实验过程较为繁琐。因此，有学者提出了单试样法的测量方法。Sumpter［10］提出了η因子的概念求解材料的J积分，并得到了广泛应用。

式中 U为载荷位移曲线积分;B为试样厚度;W为试样宽度;a为初始裂纹长度;A为裂纹体初始断裂韧带面积。

本文将使用单试样法来测定粘聚区断裂能，但单试样法公式(4)中的η因子需使用多试样法来进行标定［11］。

对比式(3)、式(4)，得η因子的公式为

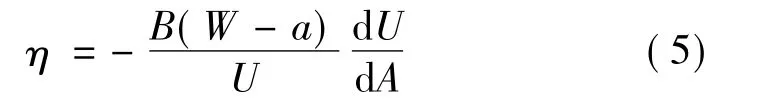
η因子的标定在20℃下展开，使用QJ 211B万能材料试验机在20 mm/min的拉伸速率进行拉伸实验，试样几何尺寸B=5 mm、W=30 mm、裂纹初始长度a不同。实验过程中记录载荷位移曲线，同时使用CCD同步测量裂纹开裂过程。使用式(5)对实验结果进行处理，可获得η因子随裂纹初始长度的关系，如图3示。从图3可发现，η随裂纹初始尺寸稍有变化，平均值变化范围包含在测量标准差之内。因此，可认为η在所取的裂纹初始尺寸范围内为恒定值。

图3 η因子与裂纹初始尺寸关系Fig.3 η factor vs initial crack size

J积分的测量使用单试样法在20℃下展开，试样的初始裂纹长度a/W=0.5，共进行5次重复性实验。实验过程中采集试样的载荷-位移曲线。对载荷-位移曲线积分，获得裂纹试样起裂时的裂尖输入能量U，结合测量的η因子代入式(4)，得到HTPB推进剂在20 mm/min的拉伸速度下的粘聚区断裂能为(1.007±0.050)N/mm。粘聚区断裂强度的测量采用标准单轴拉伸实验获取。在20℃环境温度下，进行一组20 mm/min的等速拉伸试验，得到HTPB推进剂的极限断裂强度为(0.548±0.033)MPa。粘聚区损伤函数的最终软化参数在第4章详述。

3 数值算法

本文使用 ABAQUS的用户自定义单元子程序UEL开发出粘聚区单元，用来模拟HTPB推进剂的起裂和开裂过程。用ABAQUS Standard求解时，需提供粘结单元的切线刚度矩阵和力矢量，下面将详细推导其具体形式。

根据有限元虚功原理，不考虑体力情况下，包含粘结单元的平衡方程和边界的等效弱积分形式为

式中 δεij、δi、δui分别为实体单元应变、粘结单元相对位移、边界位移;σij、Tic、Tie分别代表实体单元应力、粘结单元粘聚力、力边界;dV、dSc、dSe分别代表实体单元控制体、粘结单元表面、外边界。

式(6)中的第二项代表粘结单元的贡献部分。图4为粘结单元变形示意图。

图4 粘结单元Fig.4 Cohesive element

粘结单元相对位移为

其中:

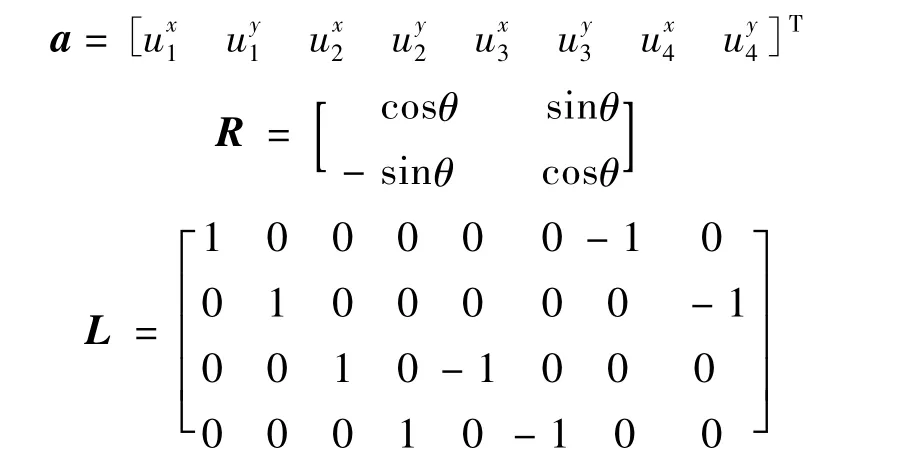
式中 a为粘结单元节点在系统坐标下的坐标值;R为坐标转换矩阵。

插值形函数为

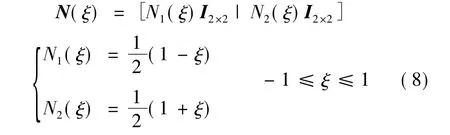
粘结单元的切线刚度矩阵可表示为

式中 C为粘结单元的Jacobian矩阵。

粘结单元所提供的力矢量表示为

ABAQUS开发过程中需提供式(9)、式(10)，系统建立起总体刚度矩阵，按Newton迭代法进行迭代求解。式(11)为系统刚度矩阵，式(12)为牛顿迭代法的计算格式。

4 仿真和模型验证

为了确定所使用的幂指数形式的粘聚区模型中的本构参数α，使用所建立的粘聚区有限元仿真方法，对包含I型裂纹的HTPB推进剂试样进行数值仿真。仿真模型为包含I型裂纹的板条形推进剂试样。试样初始裂纹长度为15 mm，上下表面施加20 mm/min等速位移载荷。HTPB推进剂是一种典型的粘弹性材料，其力学特性和加载历史存在相关性。在仿真过程中，使用线粘弹性本构来描述HTPB推进剂的力学行为。图5中，灰色区域为拉伸实验获得的载荷-时间变化范围。图5中，3条曲线分别为不同粘聚区本构参数α下通过仿真获得的载荷-时间曲线。从图5可发现，随着α的减小，仿真的最大载荷逐渐增大，断裂时间后延，但曲线之间的上升段初期基本重合，且变化趋势基本一致。通过对比发现，当α=0.55时，仿真曲线基本位于实验结果的中间部分。因此，可确定出HTPB推进剂粘聚区本构参数α≈0.55。

图5 单边裂纹载荷-时间曲线仿真值和实验值Fig.5 Numerical and experimental load-time curve of signal edge notched sample

为了验证所建立的HTPB推进剂粘聚区模型的准确性和所建立的有限元仿真方法的精确性，下面将数值仿真预测结果和实验结果进行对比。如图6所示，仿真模型左右两侧开有10 mm初始裂纹，左右裂纹上下相距20 mm。由于裂纹扩展路径未知，需在所有网格单元之间嵌入粘结单元，本文使用MATLAB编程，生成了ABAQUS识别的网格文件。图6为27 s时的仿真和实验过程中的断裂形貌。可发现，2条初始裂纹已出现扩展，试件的整体变形、裂纹扩展形貌基本一致。图6(a)给出了仿真中的Mises应力分布情况。可看到，裂纹尖端应力分布上下不对称，此时裂纹呈现出平面Ⅰ-Ⅱ型复合裂纹。

图6 t=27 s断裂形貌Fig.6 Fracture morphology at 27 s

图7(a)为仿真结束后的网格，裂纹沿初始网格界面进行扩展。由于网格布置存在一定的不对称性和计算中的舍入误差原因，仿真结果中右上部裂纹贯穿，左下角裂纹未贯穿。图7(b)为实验结束后裂纹扩展路径。由于裂纹体的不对称性，所做的3次重复性实验均呈现出如图7所示的单条裂纹贯穿情况，贯穿裂纹在扩展过程中逐渐转向。通过对比可发现，仿真预测的裂纹扩展路径和实验结果吻合良好，证明所建立的嵌入粘结单元的仿真方法，可较好地模拟出复合裂纹的扩展路径。本文仿真过程中，裂纹表面在开裂后处于自由表面状态。在真实状况下，发动机药柱在裂纹扩展过程中，伴随着燃气的窜入过程。因此，开裂后的裂纹面将处于压力载荷作用之下。如果需考虑到裂纹面内存在压力载荷的情况，需在式(10)所示的单元力矢量列阵中，加入外界压力载荷的作用项。

图7 仿真和实验裂纹开裂路径Fig.7 Numerical and experimental crack path

图8为仿真和实验获得的载荷时间曲线。图8中，灰色区域为实验测得的载荷时间变化情况，曲线为仿真预测结果。从图8中发现，仿真曲线的最高大值与实验测量结果基本一致。曲线前半部分在实验测量范围之内，说明所建立的模型对裂纹的起裂预测较为准确。曲线后半部分下降段曲线有所提前，这可能是因为实际情况下推进剂裂尖局部区域外也产生了脱湿等损伤，造成了材料整体软化、模量下降。因此，实际载荷时间曲线比预测值后移。

图8 验证试样仿真和实验载荷-时间曲线Fig.8 Numerical and experimental load-time curve of verifiable sample

综合图7、图8可发现，所建立的粘聚区本构模型和仿真方法，为HTPB推进剂裂纹起裂和裂纹扩展过程提供了一个较先进的物理模型和数值仿真方法。传统有限元计算方法在计算裂纹起裂问题时，由于裂尖应力奇异性造成了裂尖应力计算的不可信。使用粘聚区模型来模拟裂尖应力时，粘聚区本构模型的损伤特性避免了裂尖应力的奇异性，使裂尖应力更加合乎物理实际。裂纹起裂扩展后，造成了物理模型在裂尖的几何不连续性，这是传统有限元单元所无法实现的。本文建立的仿真计算方法，通过合理地构建粘结单元来模拟裂纹开裂这一物理现象，可有效地解决由于裂纹扩展所造成的几何不连续性。

实验中发现，HTPB推进剂断裂性能和断裂强度随加载速率变化，HTPB推进剂粘聚区本构也存在一定的粘弹性效用。因此，建立相关的HTPB推进剂粘聚区断裂模型将是下一步的研究重点。

5 结论

(1)建立的粘聚区断裂模型能很好地反映出HTPB推进剂裂纹起裂和裂纹扩展的失效过程。

(2)基于ABAQUS建立了模拟裂纹扩展的粘结单元，并建立了模拟复合型裂纹开裂过程的嵌入粘结单元法，使用该方法成功预测了HTPB推进剂裂纹扩展路径。

［1］李九天，雷勇军，唐国金，等.固体火箭发动机药柱表面裂纹分析［J］.固体火箭技术，2008，31(5):471-474.

［2］Earnest T E.RSRM TP-H1148 main grain propellant crack initiation evaluation［R］.AIAA 2005-3061.

［3］Barenblatt G I.The formation of equilibrium cracks during brittle fracture:general ideas and hypotheses axially-symmetric cracks［J］.Journal of Applied Mathematics and Mechanics，1959，23(3):622-636.

［4］Dugdale D.Yielding of steel sheets containing slits［J］.Journal of the Mechanics and Physics of Solids，1960，8(2):100-104.

［5］Xu X，Needleman A.Numerical simulation of fast crack growth in brittle solids［J］.Journal of the Mechanics and Physics of Solids，1994，42(9):1397-1434.

［6］刘陆广，欧卓成，段卓平，等.混凝土动态断裂数值模拟［J］.兵工学报，2010，31(6):741-745.

［7］崔浩，李玉龙，刘元镛，等.基于粘聚区模型的含填充区复合材料接头失效数值模拟［J］.复合材料学报，2010，27(2):161-168.

［8］Tabakovic A，Karac A，Ivankovic A，et al.Modelling the quasi-static behaviour of bituminous material using a cohesive zone model［J］.Engineering Fracture Mechanics，2010，77(13):2403-2418.

［9］Begley J A，Landes J D.The J integral as a fracture criterion［R］.ASTM STP 514，1972.

［10］Sumpter J D G.Elastic plastic fracture analysis and design using the finite element method［D］.London:University of London，1973.

［11］Ramorino G，Agnelli S，De R Santis，et al.Investigation of fracture resistance of natural rubber/clay nanocomposites by J-testing［J］.Engineering Fracture Mechanics，2010，77(10):1527-1536.