双曲型偏微分方程的变分迭代解法
2013-08-29黄得建李艳青
黄得建,李艳青
(琼州学院理工学院,海南 三亚 572022)
0 引言
二阶双曲型偏微分方程通常有如下形式:
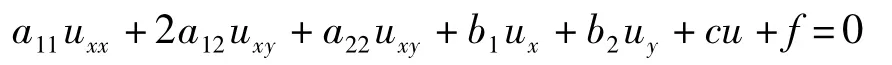
变分迭代算法是何吉欢在广义拉氏乘子法[1]的基础上提出来并进行改进[3],[2,4]中作者成功的将此法应用到一些模糊方程问题,[5]中作者将这种方法应用于生物反应模型,[6,7]分别给出了这种方法的理论依据.下面应用[3]中改进的变分迭代算法来找一类双曲型偏微分方程的精确解.
1 双曲型偏微分方程及解法分析
考虑下面的二阶偏微分方程:

其中a,b,c,f 都是关于(x,y,p)的函数,其中p=(u,ux,uy).若对任意的(x,y),都有b2-ac>0 成立,则式(1)是一个双曲型方程.
考虑双曲型偏微分方程(1)及定解条件:

或

假定式(1)中的系数与ux,yy和u 无关.若定解条件为式(2),则由变分迭代算法,可在y 一方向上构造解的校正泛函如下:
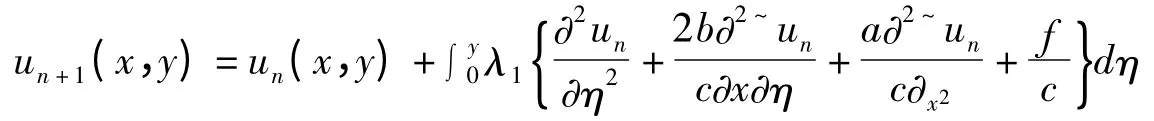
其中c≠0.应用变分迭代算法,可近似识别:λ1=η-y
假定初始近似解为

由[3]中改进的变分迭代算法,可以得到式(1)解的迭代公式如下:

同理,若定解条件为式(3),由变分迭代算法,可在方向上构造解的校正泛函:

其中a≠0.应用变分迭代算法,可近似识别:λ2=ξ-x
假定初始近似解为

可以得到式(1)解的迭代公式如下:
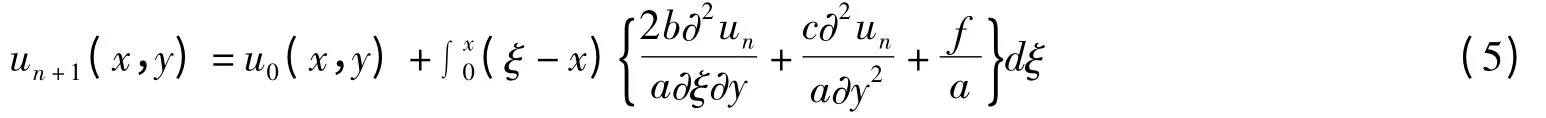
2 应用
变分迭代算法可以准确的得到上述线性双曲型偏微分方程的精确解,以下用几个例子来说明.
例1 考虑如下方程[8]:

定解条件为:

式(6)可改写为:

由变分迭代算法,可以构造y 一方向上解的校正泛函如下:

应用变分迭代算法,可近似识别:λ=η-y
假定初始近似解为:u0(x,y)=f(x)+g(x)y=3x2,
由式(4),可以得到解的迭代公式如下:

将u0(x,y)=f(x)+g(x)y=3x2代入上式,得
如表1,健康志愿者的rCBF比值范围为(1.013±0.079),ASL图左右对称,未见明显的异常灌注区;患者中TIA发作患者有15例,大面积梗塞患者11例,小面积梗塞患者14例,rCBF比值范围为(0.764±0.117),两组数据对比组间差异具有统计学意义(P<0.05)。
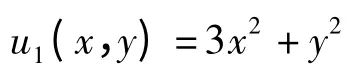
此为式(6)在满足定解条件u(x,0)=3x2,uy(x,0)=0 时的精确解.
例2 考虑如下方程[8]:

定解条件为:

式(7)可改写为:

由变分迭代算法,可以构造方向上解的校正泛函如下:
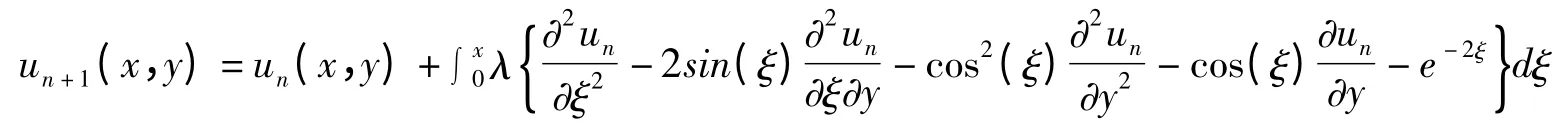
应用变分迭代算法,可近似识别:
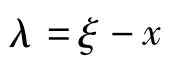
假定初始近似解为:u0(x,y)=f(y)+g(y)x=0,

将u0(x,y)=f(y)+g(y)x=0 代入上式,可得:

此为式(7)满足定解条件u(0,y)=0,ux(0,y)=0 时的精确解.
例3 考虑如下方程[8]:
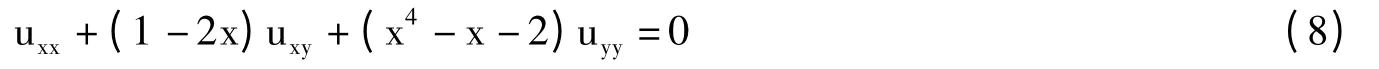
定解条件为:

由变分迭代算法,可以构造方向上解的校正泛函如下:
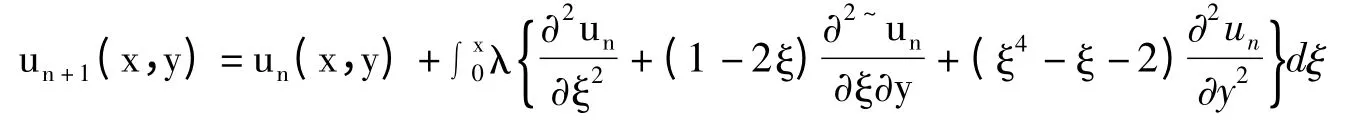
应用变分迭代算法,可近似识别:λ=ξ-x
假定初始近似解为:
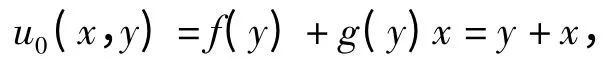
由式(5),可以得到解的迭代公式如下:

将u0(x,y)=f(y)+g(y)x=y+x 代入上式,可得:u1(x,y)=x+y
此为式(8)满足定解条件u(0,y)=y,ux(0,y)=1 时的精确解.
3 结论
把改进的变分迭代算法成功地运用到一类双曲型偏微分方程的求解,过程既简单又直观,并且收敛速度很快,计算量小、精确度高,又可以很方便的编程.
[1]M.Inokuti,H.Sekine,T.Mura.General use of the lagrange multiplier in nonlinear mathematical physics,.in:S.Nemat-Nasser(Ed.),Variational Method in the mechanics of Solids[C],New York:Pergamon Press,1978,156-163.
[2]T.Allahviranloo,S.Abbasbandy,H.Rouhparvarc,The exact solutions of fuzzy wave-like equations with variable coefficients by a variational iteration method[J].Applied Soft Computing.2011(11)2186–2192.
[3]He,J.H.,Variational iteration method-some recent results and new interpretation[J].J.Comput.Appl.Math.2007(207):3-17.
[4]Omid Solaymani Fard,Nima Ghal-Eh,Numerical solutions for linear system of first-order fuzzy differential equations with fuzzy constant coefficients[J].Information Sciences.2011(181)4765–4779
[5]S.M.Goh,M.S.M.Noorani,I.Hashimc,Introducing variational iteration method to a biochemical reaction model[J].Nonlinear Analysis:Real World Applications.2010(11):2264_2272.
[6]Zaid M.Odibat,A study on the convergence of variational iteration method[J].Mathematical and Computer Modelling.2010(51):1181_1192.
[7]Ning Chen,Baodan Tian,Jiqian Chen,A class of new fixed point theorems for1-set-contractive[J].Physics Procedia 2012(33):1932– 1938.
[8]Zhongwei Cha.Partial differential equations of mathematics and physics[M],Traffi-c university of southwest press,2005.
