凸包内空间散乱点集Delaunay四面体角度剖分算法

邵铁政，李世森

（天津大学，天津300072）

随着计算机能力的不断强大，三维空间内的有限元计算被越来越广泛的使用，因此三维空间内的网格划分也随之不断地被研究和改进。三维问题所采用的网格划分单元一般是四面体、六面体。而四面体网格具有灵活性较高及能够更好的逼近边界的特点。四面体网格生成的算法已经有许多重要的进展，如局部变换法、Delaunay 算法、四叉树/八叉树算法、单元生长法、网格前沿法等，其中以Delaunay 算法应用最广，因为其具有严谨的数学理论证明作为基础，能够由初始散乱点生成形态优化的网格，故称为Delaunay 网格［1］。

相对于二维领域而言，目前Delaunay 算法在三维领域内的研究还不够成熟，因为三维空间内，点、边、面的管理及单元之间的关系更加复杂，单元重叠的可能性较大，而且不易检验。经研究大部分Delaunay 算法［1-3］，散乱点集的外边界进行Delaunay 三角剖分,而且需要先在散乱点内部形成一个初始的四面体剖分，然后通过交换或者寻找几何关系将内部四面体的剖分更新为新的Delaunay 四面体剖分，这样使得网格划分过程的前期工作量较大。本文适用于外包面为凸的散乱点四面体剖分，不需要内部初始四面体划分，提高了四面体网格划分的效率。

1 三维散乱点Delaunay 四面体网格生成方法

1.1 相关概念

Delaunay 算法源于1934 年B.Delaunay 提出的Delaunay 准则［4］。

三维Delaunay 准则的定义如下：

（1）定义1:对于三维空间内由一堆散点组成的四面体网格，若每一个四面体的外接球均不包含除此四面体顶点以外的网格点，则此四面体称为Delaunay 四面体，由这些四面体形成的网格称为Delaunay 网格。在已知大量初始散点的情况下，若不存在多点共球的情况，则由这些散点形成的Delaunay 网格是唯一的［5-6］。

为了方便寻找Delaunay 四面体，本文引入了一个新的角度概念——球缺角。由二维Delaunay 三角形圆心角判定方法推出三维空间下的部分相关定义如下。

为了阐述方便本文引入了平面域内、域外定义：

（2）定义2:如图1-a 以平面ABC 为例，右手展开拇指与其余四指垂直，四指沿A-B-C 方向握拳，拇指所指方向的空间，即平面ABC 上部O 点所在空间为域内，反方向的空间及平面ABC 则为域外。

四面体球缺角定义如下：

（3）定义3：如图1-a，ΔABC 为在三维空间内一个三角形，D 为在空间内与之构成四面体的点，O 为A、B、C、D 四点的外接球球心，半径为R。OA 为O 与ΔABC 任意顶点形成向量，则OA与ΔABC 的负法向量n的夹角就是点D 对ΔABC 的球缺角δ(0＜δ＜π)。

（4）四面体球缺角的特性1:由以上定义易知D 对ΔABC 的球缺角δ 唯一。

（5）四面体球缺角的特性2:在空间内当所有散乱点位于ΔABC 域内，一点与已知三角形构成Delaunay 四面体的条件是：这个点对ΔABC 的球缺角最大。

1.2 相关证明

（1）特性1 证明:根据定义3 可知，四面体球缺角即为球心与三角形所构成的圆锥的圆锥角的一半，所以得证。

（2）特性2 证明:图1-b 为图1-a 的正视图，球O 过A、B、C、D 四点，r 为已知ΔABC 外接圆半径，R 为球O 的半径，h 为O 到ΔABC 的距离，H 为ΔABC 域内球缺高，则球缺的体积

若D-ABC 为Delaunay 四面体，则根据[定义1]只需证明球缺内不包含任何点。若证明[特性2]，只需证明球内任意点D1对ΔABC 的球缺角大于D 对ΔABC 的球缺角即可。

∵h=r×cotδ，R=r/sinδ，H=h+R

∴球缺体积V（δ）=（r/sinδ+r×cotδ）2×[3×（r/sinδ）-（r×cotδ+r/sinδ）] ×π/3

=（-cos3δ+3×cosδ+2）×πr3/（3×sin3δ）

由以上推导公式可知:

对于已经固定的ΔABC 外接圆半径r 不变，即球缺体积为以δ 为自变量的函数，则可求出并化简得到V-δ 函数的一阶导数

V′（δ）=-（1+cosδ）2×πr3/sin4δ

∴由于(0＜δ＜π)，V′＜0

得证V 与δ 反相关

如图1-b 易知在域内，D1点对ΔABC 的球缺体积必然小于点D 对ΔABC 的球缺体积。即D1点对ΔABC球冠角δ 更大。

当域内球缺小于半球时，δ 的范围是（π/2，π），即cotδ 为负，证明过程相同。

所以［特性2］得证。

2 编程实现散乱点四面体划分的步骤

2.1 散乱点数据读入

数据文件要求：散乱点按统一格式存入inputA.txt 文件中，顺序为“初始点号，x 坐标，y 坐标，z 坐标”。

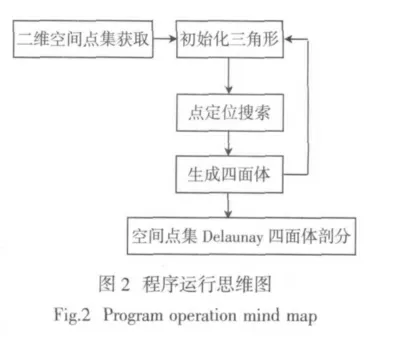
2.2 程序运行思维图

如图2 所示，程序运行分为以下几个步骤：

（1）三维空间点集获取：读取输入文件中的所有点的坐标，读取内容包括“初始点号，x 坐标，y 坐标，z 坐标”。

（2）初始化三角形：读取文件中的第一、二、三点为初始三角形。

（3）点定位搜索：由初始三角形根据四面体球缺角的特性2 在散乱点中寻找与之构成Delaunay 四面体的点，并生成Delaunay 四面体。

（4）循环运行搜索：在生成每一个四面体的同时，有3 个新的三角形生成，分别以新生成的三角形为初始三角形继续寻找对应的点。由此循环运行直至将所有的散乱点进行四面体划分。

2.3 搜索方法

步骤（3）中搜索方法分为以下几个部分：

（1）确定搜索区域:为减少程序的运算量，将所有散乱点分为域内、域外2 个部分（方法见3-(3)）,只对域内部分进行搜索。

（2）计算球心坐标：分别将域内的所有点按顺序分别与初始三角形的3 个顶点组合，由子程序计算此空间四点的外接球的球心坐标O。

（3）计算保存向量：根据三角形顶点坐标求出三角形外接圆圆心坐标O1，向量OO1即为初始三角形负法向量。保存球心O 与任意三角形顶点形成的向量OA (根据[特性一]，O 与任意顶点形成的向量与OO1夹角大小相同)。

（4）计算OA 与OO1夹角

计算出OA 与OO1夹角，并保存，以便经历一次搜索后找出最大的夹角，并确定为最大球缺角，该角对应的点与此初始三角形构成Delaunay 四面体。

3 程序的准确性和高效性

为提高程序运行的准确性和效率，本程序进行了以下几方面的处理:

（1）顺序记录：在每次计算所得的新三角形点数据，都按照顺时针方向进行记录,保存的新生成的数据格式符合初始运算格式，使程序可以循环进行计算。

（2）查重：由于初始三角形不同，对于每次生成的新的四面体来说有可能与前面生成的四面体重复，因此，对新生成的四面体进行查重，假设生成的新四面体4 个点的序号分别为（a，b，c，d），将(a，b，c，d)分别与之前生成的各数组对比，如果出现与（a，b，c，d）数值构成相同的数组，则取消该四面体，不存入，由此循环下去，并不断检验是否重复，直到令所有点都找到Delaunay 四面体则计算过程结束。

（3）域内域外判断：对于新生成的三角形来说一部分点位于该三角形的域内，另一部分位于域外。本程序对所有点与初始三角形的位置关系进行了预判，域外的三角形不必要进行复杂的计算，因此提高了程序的运行。四面体体积判定法:根据三维行列式正负的意义，A（x1，y1，z1）、B(x2，y2，z2)、C（x3，y3，z3)为空间的三点，D（x0，y0，z0）与三点的行列式表示的是四面体的体积（当D 位于平面ABC 的域内时V 为正，否则V 为负）。

四面体体积

（4）避免计算误差：本文采取了一系列方法避免计算过程中产生的误差，其中以下2 个方法用于整个程序中相关的计算步骤。①为避免计算机在计算时出现除以0 的数学错误，本程序在编译时避免了除法运算，全部使用正负号的判断，避免了计算机储存或计算中出现误差的情况。②在步骤（2）、（3）中计算球心、外接圆圆心时，本程序采用克拉默法则对方程组进行求解，但是在程序编译过程中发现，编程平台自带的IMSL 函数库在计算行列式过程中DET（）函数使用lin_sol_lsq（）来解方程［7］，对于行列式值为0 或非常接近于0 的矩阵会失效，所以本程序中使用了重新编译的行列式计算函数进行相关计算，消除了此类计算误差。

4 时间复杂度分析

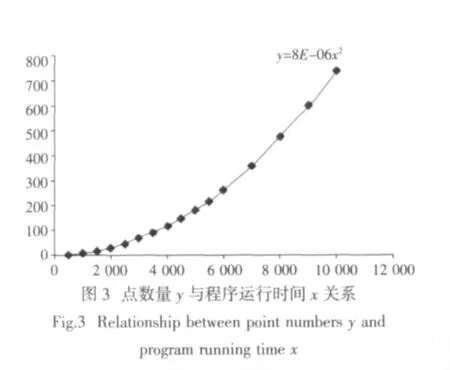
为了对本程序的计算效率进行比较，本文进行了程序运行时间复杂度的分析［8］。图3 为不同点数的情况下程序运行时间的趋势线情况。

根据趋势线可以看出计算的点的数量y 与程序运行时间x 的关系拟合曲线为y=8E-06x2，即时间与点数总量呈二次关系，该计算方法有良好的应用特性。

5 结束语

球缺角定义的提出，使Delaunay 四面体的剖分有了更加量化的方法，区别于以往的定性判断，量化的方法误差更小，更容易控制和比较。虽然在本方法的实践过程中仍有一些方面不完善，但是相信在不断地改进后，将对空间散乱点集Delaunay 四面体剖分方法的研究做出贡献，可用于各个领域的工程应用软件的开发。

［1］关文革，武强，贾丽萍，等.约束数据域Delaunay 四面体网格生成算法［J］.华中科技大学学报：自然科学版，2005（5）:67-69.GUAN W G，WU Q，JIA L P，et al. Algorithm of mesh generation of Delaunay tetrahedral in constrained domain［J］. Journal of Huazhong University of Science and Technology，2005（5）: 67-69.

［2］WU Q，XU H.An approach to computer modeling and visualization of geological faults in 3d［J］.International Journal of Geographical Information Systems，1993，7（6）:501-524.

［3］XU H，WU Q.Design & implementation of visualization for 3d samdwich geological bodies［J］. Computer Applictations，2001，21（12）:56-60.

［4］Lawson C L. Software for C1 surface interpolation，Mathematical Software III［M］. New York: Academic Press，1977: 161-194.

［5］陈学工，潘懋.空间散点集Delaunay 四面体剖分切割算法［J］.计算机辅助设计与图形学报，2002（1）:93-95.CHEN X G，PAN M. Delaunay Triangulation Cutting Algorithm for A Set of Irregularly Located Spatial Points［J］. Journal of Computer Aided Design & Computer Graphics，2002（1）: 93-95.

［6］王建华，徐强寻，张锐.任意形状三维物体的Delaunay 网格生成算法［J］.岩石力学与工程学报，2003，22（5）:717-720.WANG J H，XU Q X，ZHANG R. Delaunay algorithm and related procedure to generate the tetrahedron mesh for an object with arbitrary boundary［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（5）:717-720.

［7］李丽.三维空间Delaunay 三角剖分算法的研究及应用［D］.大连：大连海事大学，2010.［8］彭国伦.Fortran95 程序设计［M］.北京：中国电力出版社，2010.