高桩码头接岸结构尺度对岸坡稳定性影响及其优化研究

张雯雯，别社安，余神光

（1. 天津大学 建筑工程学院，天津300072；2. 中交第四航务工程勘察设计院有限公司，广州510230）

高桩码头是我国港口中应用最广泛的码头结构型式之一［1］，适用于软土层较厚，适合打桩的地基。高桩码头具有投资省、便于施工、使用和维护经验丰富等特点，多年来一直是天津港地区的主导结构型式。重力式挡土墙接岸结构［2］是高桩码头接岸结构中最广泛使用的一种，由斜坡堤、护面和堤顶的挡土墙结构等组成，有着施工简单、耐久性好、不需要复杂的施工设备等优点，其缺点是码头岸坡较缓，宽度较大，导致码头后方承台宽度大，造成工程投资不经济。高桩码头的接岸结构和后方承台一般占码头投资的30%～50%。所以如果在保证岸坡稳定的情况下，适当减少接岸结构的尺度，从而降低后方承台的宽度，就可以提高码头的总利用率，减少码头结构的后期维护工作量，对节省工程投资具有重要意义。

1 高桩码头岸坡优化方法

针对边坡稳定性计算［3］，与目前常用的极限平衡法相比，有限元方法适用性广，可视性强，可以考虑土体的非线性本构关系以及变形对应力的影响，并有助于了解边坡的渐进破坏机理。本文研究主要围绕天津港高桩码头的岸坡整体稳定性问题，通过有限元强度折减法［4］（PLAXIS 软件）对不同规模的高桩码头接岸结构的尺度和后方承台宽度进行优化。

1.1 有限元建模假设

在使用PLAXIS 有限元软件做数值模拟计算过程中，采用了如下假设：

（1）假设地下水位为设计低水位；

（2）不考虑高桩码头桩基对岸坡整体稳定性的影响；

（3）土体假设为匀质，地基初始应力产生仅与土坡自重有关；

（4）假设墙前淤泥的粘聚力随深度增加而线性增加，具体参数详见表1；

（5）为方便计算，将岸坡几何模型简化为二维平面应变问题进行处理。

1.2 有限元强度折减法介绍

有限元强度折减法是指将土体的强度参数C 和φ 同时除以一个折减系数F，得到一组新的C′和φ′，然后再对边坡进行有限元分析，通过不断增大折减系数使边坡达到临界破坏状态，把此时的折减系数作为安全系数。对M-C 材料，折减系数可表示为

式中：c 为土体的粘聚力；φ 为土体的内摩擦角；F 为强度折减系数；c′、φ′分别为折减后的强度参数。

1999 年，美国科罗拉多矿业学院Griffith［5］等人采用有限元强度折减法与传统方法得到的稳定安全系数进行比较，结果比较接近。根据对比计算结果［6］，有限元算法结果与规范中的简单条分法的结果存在较小的差异，如依据目前规范的规定，若将有限元计算出的岸坡整体稳定结果用于工程实际，按95%置信度考量，其安全系数需进行10%的折减，即有限元得出的安全系数在1.1 以上为安全。

1.3 有限元中边坡破坏的判定依据

采用有限元强度折减法分析岸坡的一个关键性的问题是如何根据计算结果来判别岸坡是否处于整体破坏状态。目前主要的判断边坡失稳的判据［7］主要有以下几种：

（1）以有限元数值计算的不收敛性作为岸坡失稳标志；

（2）以岸坡特征部位位移的突变临界点作为失稳标志；

（3）以塑性区从坡脚到坡肩的贯通作为失稳标志。

目前相关研究对采用何种标准尚未取得统一，但是目前多以塑性区的贯通［8］作为标准。

2 高桩码头岸坡尺寸优化

2.1 建立初始模型

本文将运用PLAXIS 有限元软件，采用其中的Mohr-Coulomb 模型，分别针对天津港5 万t 和10 万t 级散杂货高桩码头，建立高桩码头岸坡的数值模分析模型，接岸结构为重力式挡土墙型式，码头-岸坡断面示意图如图1 所示，土体主要参数见表1，有限元计算结果位移云图如图2 所示。以下10 万t 级散杂货码头为例进行优化。

表1 地质参数Tab.1 Geological parameters

2.2 挡土墙高度h 和挡土墙宽度b 对岸坡稳定性的影响

为了探究重力式挡土墙尺寸对岸坡整体稳定性的影响，进行如下分析：

选取10 万t 级散杂货码头岸坡，针对坡比1:3、坡肩宽度48 m 的岸坡尺寸，在4 种不同坡肩泥面高程（+1.0 m、0 m、-1.0 m、-4.0 m）情况下，分别改变挡土墙的宽度、高度，研究挡土墙的尺寸对岸坡稳定安全系数的影响。另外为排除固定坡比和坡肩宽度的影响，另选择坡比1:2.5、坡肩宽度30 m 的岸坡尺寸，在坡肩泥面高程+1.0 m 的情况下予以验证。

由计算结果表2、表3 可知，对于高桩码头的接岸结构，在其他条件不变情况下，改变挡土墙高度h 或挡土墙宽度b，对码头岸坡稳定安全系数的影响不大。因此遵循既满足挡土墙自身抗滑、抗倾稳定性要求，又满足工程造价最低的原则，可得到10 万t 级散杂货高桩码头重力式挡土墙接岸结构最优挡土墙尺寸（如表4所示）。

表2 坡比1:3、坡肩宽度48 m 方案下，不同泥面下挡土墙尺寸对岸坡整体稳定性的影响Tab.2 Effect of retaining wall scale on stability of the whole bank in different mud surface with 1:3 slope ratio and 48 m slope shoulder width m

表3 坡比1:2.5、坡肩宽度30 m 方案下，+1 m 泥面下挡土墙尺寸对岸坡整体稳定性的影响Tab.3 Effect of retaining wall scale on stability of the whole bank in +1 m mud surface with 1:2.5 slope ratio and 30 m slope shoulder width m

表4 10 万t 级散杂货高桩码头不同坡肩泥面高程下最优挡土墙尺寸Tab.4 Optimal retaining wall scale of 1million-ton bulk cargo high piled wharf m

2.3 坡肩宽度B 对岸坡稳定安全系数的影响

高桩码头岸坡肩宽度B，对于码头岸坡稳定性具有重要影响。对坡肩宽度进行优化研究，对于减少码头岸坡宽度L 和缩减后方承台造价具有重要意义。选取10 万t 级散杂货码头岸坡，分别在坡比1:3 情况下改变坡肩宽度，在4 种不同坡肩泥面高程（+1.0 m、0 m、-1.0 m、-4.0 m）情况下，研究坡肩宽度B 对岸坡稳定安全系数的影响。计算结果（表5）表明，随着坡肩宽度B 的减小，岸坡稳定安全系数也在不断减小。

2.4 岸坡坡比对岸坡稳定安全系数的影响

作为高桩码头岸坡特征尺度之一的岸坡坡比，对于码头岸坡整体稳定性也具有重要影响，合理的岸坡坡比可以减少码头岸坡宽度L，从而降低后方承台的宽度及造价。选取10 万t 级散杂货高桩码头，分别在给定的坡肩宽度B 情况下，改变岸坡坡比，在4 种不同坡肩泥面高程（+1.0 m、0 m、-1.0 m、-4.0 m）情况下，研究岸坡坡比对岸坡稳定安全系数的影响。计算得出各种情况下的码头岸坡稳定安全系数。计算结果（表5）表明，随着坡比的增大，岸坡稳定安全系数在不断减小；随着坡肩宽度的减小，岸坡稳定安全系数的减小更加明显。

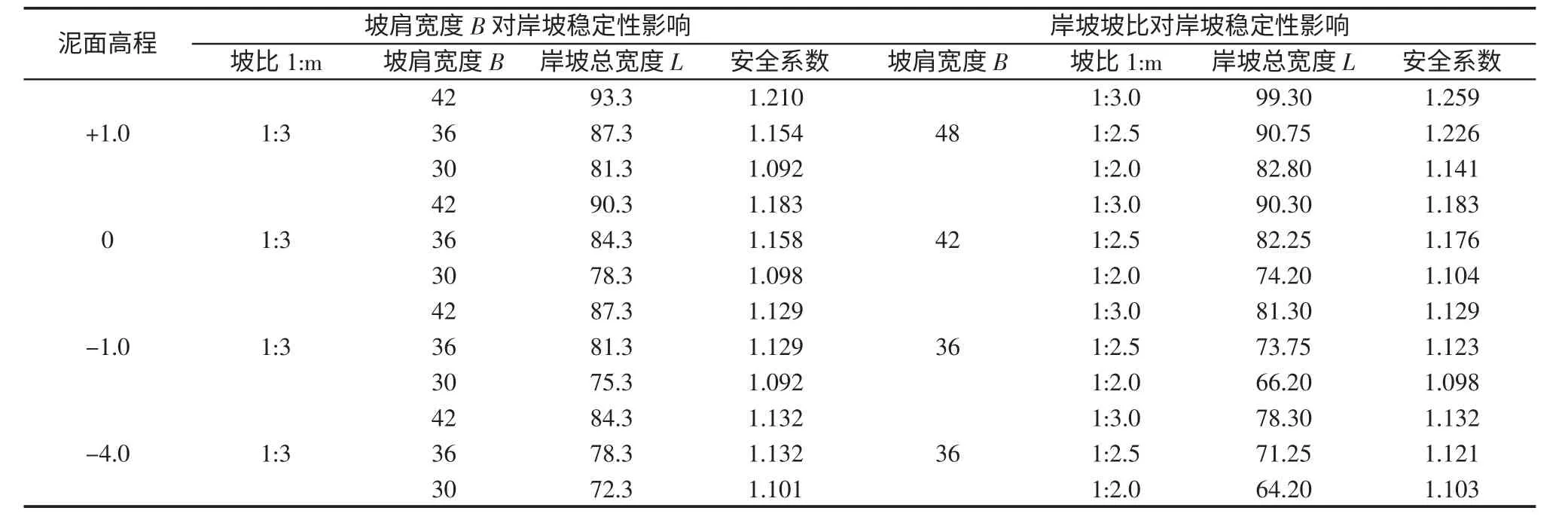
表5 岸坡尺寸对岸坡稳定性影响Tab.5 Effect of bank scale on bank slope stability

2.5 岸坡优化结果

综上所述，针对重力式挡土墙接岸结构的码头岸坡，挡土墙的尺寸变化对于码头岸坡优化的作用不明显，因此挡土墙尺寸根据自身稳定性得出。而岸坡稳定安全系数随着坡肩宽度B 的减小、坡比的增大，而不断减小。

因此，可以得出10 万t 级散杂货高桩码头不同泥面下的最优岸坡断面尺寸，及相对原始泥面设计下节约的工程造价(已包括挖泥造价)，同理，也可计算出5 万t 级散杂货高桩码头不同泥面下的最优岸坡断面尺寸，及相对原始泥面设计下节约的工程造（表6），不难看出，适当地增加挖泥深度，增大挡土墙前后泥面高差，虽然相对于原始泥面增加了挖泥的工程量，但后方承台宽度的缩减所减少的造价足以弥补挖泥所多出的造价。但前方泥面也不宜太低，从表6 中不难看出，10 万t 级散杂货高桩码头-1.0 m 与-4 m 相比节约的造价并没有变化太多，因此依据工程量比较，10 万t 级散杂货高桩码头的较适宜泥面为-1.0 m。同理可以看出5万t 级散杂货高桩码头的较适宜泥面为0 m。

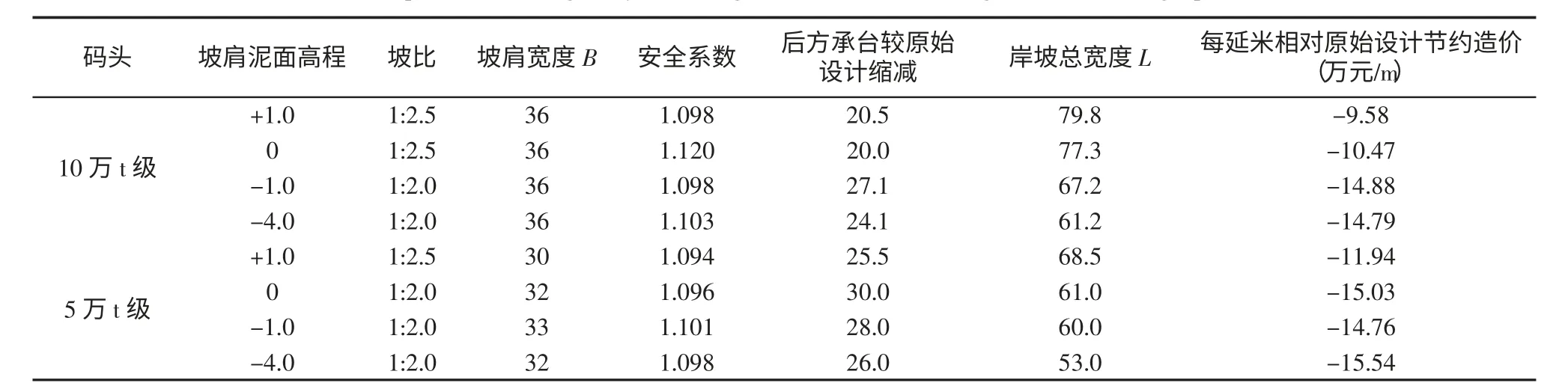
表6 高桩码头重力式挡土墙接岸结构优化Tab.6 Optimization of gravity retaining wall shore-connecting structure of high piled wharf m

3 结论

（1）基于PLAXIS 的有限元强度折减法对高桩码头岸坡稳定性的判别和优化具有可视性强，便于观察应力与破坏机理等优点。

（2）基于PLAXIS 的码头接岸结构岸坡优化结果表明，在保证岸坡稳定的前提下，适当加大挡土墙前后泥面高差，可以减小岸坡坡肩宽度和岸坡坡比，有效减小后方承台的宽度，从而达到节省工程投资的目的，并且在使用阶段提高了码头的总利用率，减少了码头结构的后期维护工作量。

［1］郭莲清.天津港码头结构综述［J］.港工技术，2001（12）：63-71.GUO L Q.General Descriptions on Wharf Structures of Tianjin Port［J］.Port Engineering Technology，2001（12）:63-71.

［2］JTS167-1-2010，高桩码头设计与施工规范［S］.

［3］史恒通，王成华.土坡有限元稳定分析若干问题探讨［J］.岩土力学，2000，21（2）：152-155.SHI H T，WANG C H.Some problems in finite element analysis of slope stability［J］.Rock and Soil Mechanics，2000，21（2）:152-155.

［4］张宝华，黄宏宝.强度折减有限元法分析码头岸坡稳定［J］.水道港口，2006，27（3）：185-187.ZHANG B H，HUANG H B.Strength reduction finite elements analysis on bank stabilization［J］.Journal of Waterway and Harbor，2006，27（3）:185-187.

［5］Griffiths D V，Lane P A. Slope stability analysis by finite elements［J］.Geotechnique，1999，49（3）：387-410.

［6］余神光.高桩码头岸坡稳定分析理论与优化设计研究［D］.天津:天津大学，2012:16-18.

［7］郑颖人，赵尚毅.有限元强度折减法在土坡与岩坡中的应用［J］.岩石力学与工程学报，2004，23（19）：3 381-3 388.ZHENG Y R，ZHAO S Y.Application of strength reduction FEM in soil and rock slope［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23（19）:3 381-3 388.

［8］刘金龙，栾茂田，赵少飞.关于强度折减有限元方法中边坡失稳判据的讨论［J］.岩土力学，2005，26（8）：1 345-1 348.LIU J L，LUAN M T，ZHAO S F.Discussion on criteria for evaluating stability of slope in elastoplastic FEM based on shear strength reduction technique［J］.Rock and Soil Mechanics，2005，26（8）:1 345-1 348.