考虑流固耦合影响的水中桩基结构振动特性分析

王元战，王朝阳

（天津大学 建筑工程学院天津市港口与海洋工程重点实验室，天津300072）

近年来港口工程呈现着向深水发展的趋势，从国内外已有工程实践看，典型的离岸深水结构是柔度较大的全直桩承台式结构［1-2］，其自振周期较长，结构的动力响应、波浪与结构动力相互作用等问题突出。离岸深水结构相对于传统近岸结构其水深较大，水体将影响结构的动力特性。对于此类水下结构的设计，不仅要考虑结构物在空气中的振动问题，而且要考虑结构物与流体耦合时的振动问题［3］。只有合理考虑水体对结构基频及阻尼比等振动特性的影响，才能保证结构设计合理、使用可靠。因此研究水体对结构振动特性的影响，具有实际的工程意义。

由于工程实践需要，自20 世纪30 年代起，国内外不少学者曾对水中柱体的振动问题做过理论和试验研究，如Yu 和Ursell、Kim、张悉德、丁思远等的工作［3-7］。这些研究大多基于势流理论，假定水是理想的不可压缩的无粘性流体，分析水体的附加质量效应对结构基频的影响；或仅定性分析水体粘性对水中结构振动阻尼比的增大效应。结构在水中振动属于典型的流固耦合问题，以往研究大多忽略了二者的相互作用效应，对水深、桩径、抗弯刚度、上部结构等相关因素的影响尚缺乏进一步的研究，对水体引起的结构阻尼比增大效应尚缺乏定量分析。因此考虑水体-结构流固耦合作用，分析水体对结构振动特性的影响，是有待研究的课题。

本文利用大型有限元软件ADINA，以一顶端伸出水面的桩柱式结构为研究对象，建立水和桩基结构的流固耦合数值模型。通过对水中桩基结构的振动特性进行数值模拟分析，探讨了水体对结构自振特性、阻尼比的影响，并给出港口离岸深水结构中水体产生的阻尼比推荐值，为工程设计提供参考和依据。

1 数值计算方法

水体采用ADINA 提供的流体运动的粘性流控制方程，即Navier-Stokes 方程。在对粘性流控制方程进行时间离散时，采用ADINA-Composite 格式，具有二阶时间精度，且无条件L-稳定［8］。采用ALE 方法模拟自由表面，通过FSI 边界来模拟水体和桩体的相互作用。

1.1 控制方程

计算域由Ω 表示，边界由Γ 表示，则非定常粘性流不可压缩流动的控制方程为

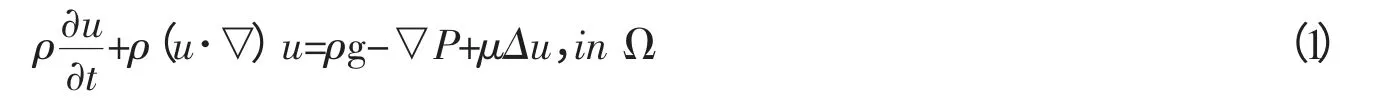
式中：ρ 为流体的密度；u 为流速矢量；g 为重力加速度；P 为压强；μ 为流体的运动粘滞系数。

1.2 控制方程的时间离散格式

在计算时采用具有二阶时间精度的ADINA-Composite 格式，该格式通过两步来计算t+Δt 时刻的速度

式中：ut+βγΔt=（1-β）ut+βut+γΔt，γ=2-1/α，β=α2/（2α-1）。如果1/2＜α＜1，则该复合格式具有二阶的时间精度，且无条件L-稳定，这里取α=1/ 2。

1.3 自由表面边界条件

在处理自由表面边界条件时采用ALE 方法，自由液面是一个移动的边界，需要满足运动边界条件和动力边界条件。运动边界条件指流体质点不能流出液面，动力边界条件表示为流体在自由表面上的压强等于大气压强，即

1.4 流固耦合界面

在流固耦合界面上，水体和结构的接触面需要满足力学和运动学耦合条件，因此接触界面需要满足力学和运动学耦合条件。力的平衡条件为

式中：σf为流场应力；σs为结构的应力张量；nc为流固耦合接触面的法向量。

对于粘性流体，假定流固耦合接触面上满足无滑移条件

式中：uf为耦合接触面的流场速度；ds为耦合接触面的结构位移。

2 有限元模型及验证

本文以一底端嵌固，顶端自由的大直径钢管桩为研究对象，通过设置FSI 边界来模拟水体和桩柱的流固耦合效应。钢管桩直径取1.8 m，壁厚22 mm，高度为32.2 m。将钢管桩视为弹性结构，考虑到其壁厚较薄，采用4 节点壳单元来模拟。流体域平面尺寸为10 倍桩径的圆，采用8 节点六面体FCBI 单元模拟流体。为考虑水体粘性引起的阻尼比增大，水体采用不可压缩粘性流，以更真实的模拟水体。流体域边界为：底边界采用可滑移固壁边界，即边界上的法向速度为零；顶边界采用自由表面边界，侧边界采用一致流边界，以模拟无限远处的边界条件。计算时钢材参数为：弹性模量E=2.1×1011Pa，密度ρ=7 850 kg/m3；流体参数：海水密度ρ=1 025 kg/m3，粘滞系数μ=1.01×10-3kg/m·s-1。本文建立的桩基结构与水体相互作用有限元模型如图1 所示。

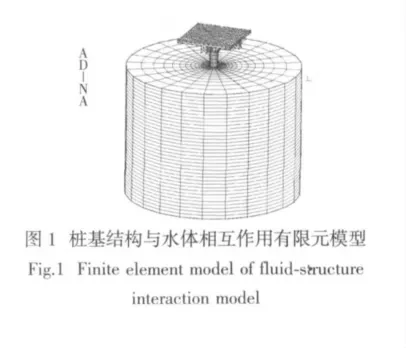
为验证本文所建立模型的正确性，根据文献［9］中的模型试验条件建立考虑流固耦合效应的水体-结构相互作用数值模型，并将数模计算结果与模型试验结果进行对比分析。数模计算结果和试验结果见表1。

由表1 可知，数模计算结果与试验结果基本相同，验证了本文所建立的考虑流固耦合作用的有限元模型的可信性。

3 考虑流固耦合影响的桩基结构基频分析

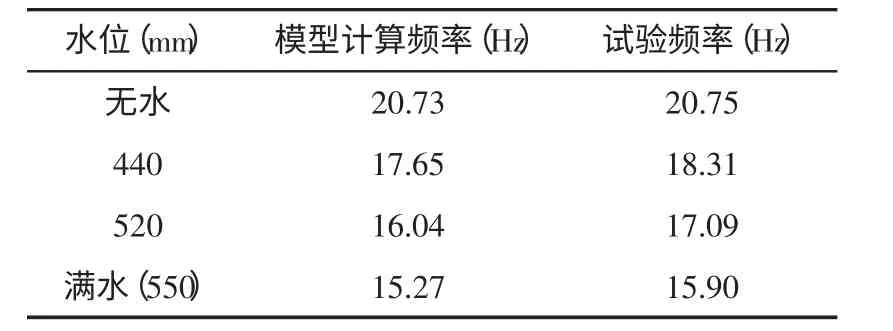
表1 数模计算结果与试验结果对比Fig.1 Contrast of numerical analysis and model test results

3.1 水深与桩长之比d/L 的影响

相关研究［5-6］表明，水对柱体的影响相当于附加在柱体上的分布质量，因此，水中柱体自振频率比无水时降低。但对于水深淹没深度对于桩体自振特性的影响程度，尚缺乏进一步的研究。为了分析水深对桩基结构自振特性的影响，在桩长一定的情况下不考虑上部结构，水深d 与桩长L 的比值依次取0.0、0.125、0.25、0.375、0.5、0.625、0.75、0.875、1.0，对桩基结构进行考虑流固耦合作用效应的自振特性分析。考虑流固耦合作用的结构1 阶振型如图2 所示，不同水深情况下结构的基频变化情况如图3 所示。

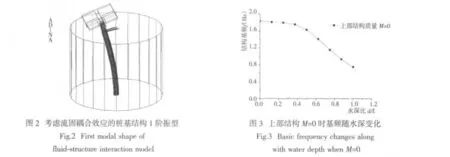
由图3 可知，考虑流固耦合相互作用后，桩基结构的横向振动的基频相对无水情况减小，其减小幅度随着水深比d/L 的增大而增加。水深比d/L 小于0.5 时，结构基频随水深增加而减小的幅度较低，曲线变化较平缓；水深比d/L 大于0.5 后，结构基频随水深增大而减小的幅度增大，曲线斜率迅速增大，下降趋势明显，桩完全被水淹没时，基频降至最小。上部结构质量为零，结构淹没时的基频相对无水情况减小幅度为59.32%。

3.2 不同上部结构对基频减小量的影响

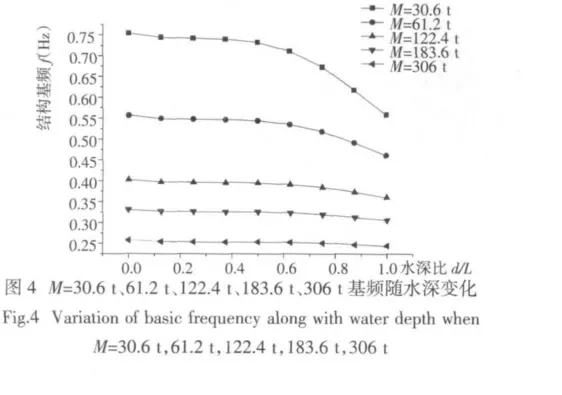
为了研究上部结构对桩基结构振动特性的影响，保持桩基不变的情况下，通过给上部结构赋予不同质量，来模拟不同的上部结构型式。上部结构的质量M 分别取0 t、30.6 t、61.2 t、122.4 t、183.6 t、306 t，通过考虑流固耦合效应的自振特性分析，来研究不同上部结构的基频随水深比d/L 减小的情况。其计算结果如图4、图5所示。

综合分析图3 和图4 可知，不改变桩基情况下改变上部结构，其基频随水深比d/L 增大均呈降低的趋势。在上部结构质量较小时，结构基频随水深比d/L 增大而降低的幅度较大，降低的趋势比较明显；上部结构质量较大时，结构基频随水深比d/L 增大而降低的幅度有所减小，降低的趋势趋于平缓。

定义结构基频降低程度a 如下

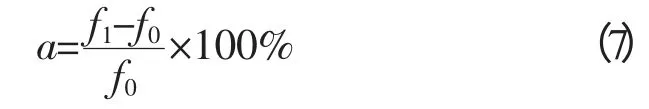
式中：f1为某一水深比d/L 对应的结构基频；f0为水深比d/L=0 时的结构基频。

则上部结构取不同质量，d/L=1 时a 随质量变化曲线如图5 所示。

由图5 可看出，考虑流固耦合作用时桩基结构基频降低程度随着上部结构质量的增大而减小，随着上部结构质量增加减小趋势逐渐趋于平缓。

3.3 不同桩基抗弯刚度的影响

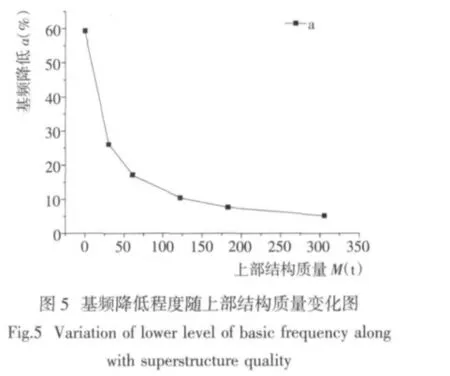
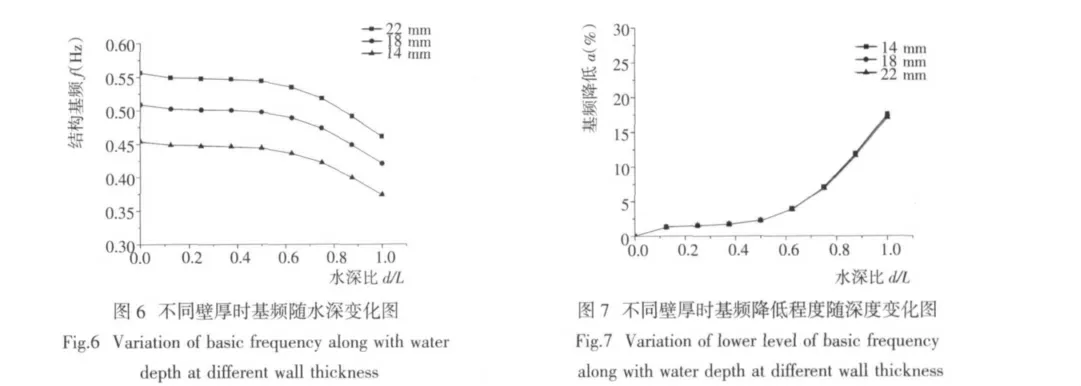
为了研究桩基抗弯刚度对结构振动特性的影响，保持桩径D=1.8 m、桩长L=32.2 m 不变的情况下，通过改变壁厚来改变桩基的抗弯刚度。取上部结构质量M=61.2 t 时进行分析，钢管桩壁厚分别取14 mm、18 mm、22 mm，则不同水深情况下结构基频计算结果见图6、图7。

由图6 可知，在桩径不变的情况下，随着壁厚的增大，结构的抗弯刚度增加，基频也随之增大，且不同壁厚时结构基频均随水深比d/L 增大而减小。由图7 可看出3 条曲线基本重合，即在不同壁厚情况下，同一水深比d/L 所对应基频相对于无水情况的降低幅度基本相同。由此可知，在桩径和上部结构不变情况下，桩的壁厚改变对基频降低程度的影响可以忽略。

3.4 不同桩径的影响

为了研究桩基直径对结构振动特性的影响，保持上部结构不变的情况下，通过改变桩径来研究桩径变化对桩基结构自振特性的影响。从国内外已有工程实践看［1-2］，港口工程离岸深水结构中所采用的桩径介于1.2～2.4 m，上面分析可知钢管桩壁厚变化对于基频降低程度的影响可忽略不计，故桩径分别取1.2 m、1.8 m、2.4 m，壁厚均取22 mm。

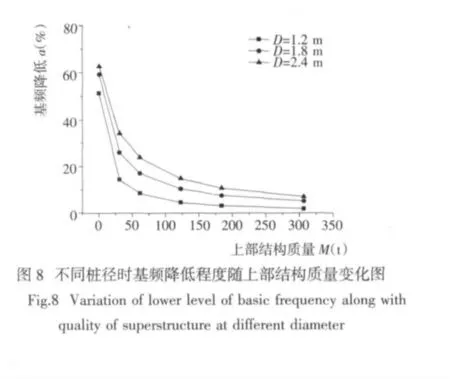
对不同桩径的结构，分别改变上部结构的质量并计算水深比d/L=1 时结构基频降低程度a1，计算结果如图8 所示。

由图8 可知，不同桩径情况下，桩基结构基频降低程度均随上部结构质量的增加呈递减趋势，桩径越大则结构基频降低程度越大，说明桩径大的结构基频受水的影响较桩径小的结构要大。

港口工程离岸深水结构其水深与桩长之比d/L 一般都在0.8 以上，考虑流固耦合效应则结构基频相对于无水情况有明显降低的趋势。特别是对于上部结构质量较小的如系缆墩等全直桩结构，考虑流固耦合后其基频降低幅度较大，使结构周期明显增大，流固耦合的影响不容忽视。因此，对于港口工程中水深较大的桩基结构的振动特性分析时，应考虑流固耦合作用的影响。

4 水体对桩基结构振动阻尼比的影响

结构在振动中阻尼的大小可以归结为耗能量的大小，结构中的阻尼有2 种，即结构材料的内阻尼和与周围介质之间产生的外阻尼。结构在一定的环境介质中工作，环境介质将显著影响结构的阻尼［3］。本文通过建立结构在水中振动的数值模型，来分析水体对桩基结构阻尼比的影响。

为计算结构振动过程的阻尼比，采用敲击法对桩基结构进行激振，给结构施加一个持续一段时间的横向冲击荷载，让结构在冲击荷载作用后进行自由振动。由此得到结构横向振动的水平位移衰减曲线，采用对数衰减法计算结构振动过程中的阻尼比［10-11］。

4.1 水体对结构阻尼比的影响

为研究水体对结构阻尼比的影响，分别对有水情况和无水情况结构振动进行数值模拟。给结构顶部以作用时间0.2 s 的冲击荷载，让结构做自由振动，采用隐式复合积分计算结构顶部水平位移时程曲线。有水情况时，水深取28.82 m、桩长33.2 m、桩径1.8 m，水温20 ℃，其粘性系数取1.002×10-3N·S/m2。计算结果见图9～图11。

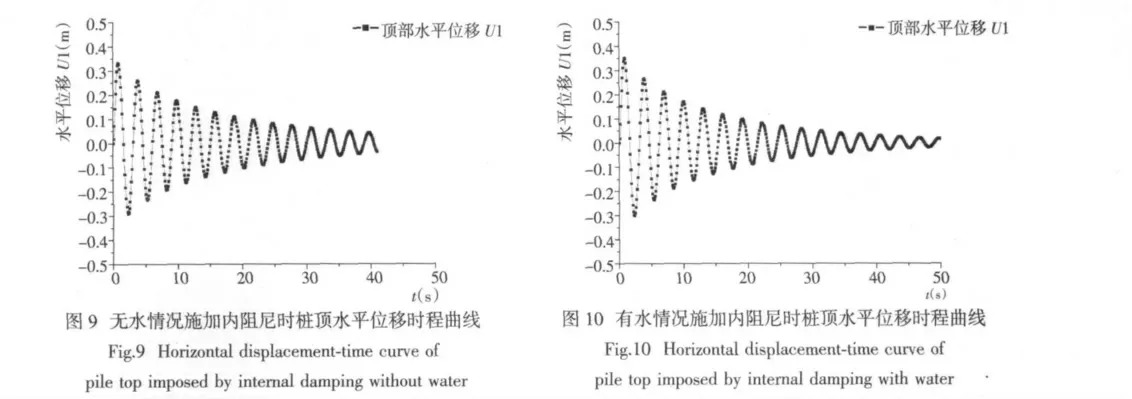
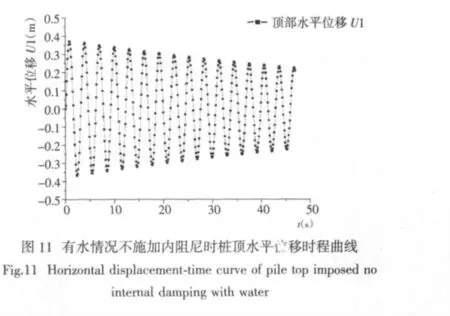
根据以上结构的水平位移时程曲线，利用对数衰减法计算相应的阻尼比。无水情况结构的阻尼比为ζ2=0.023 4；有水情况只考虑水体产生的外部阻尼，计算得到的阻尼比为ζ1=0.005 4；有水情况同时施加结构内阻尼，计算得到的阻尼比为ζ3=0.028 7。

计算结果表明，水体的存在使结构的阻尼比有较明显的增大，对于水中振动的结构进行动力分析时，应考虑水体引起的阻尼。结构在水中振动时的阻尼包括水体引起的外阻尼和结构材料的内阻尼，二者可以线性叠加，即单独由水体产生的阻尼与结构材料的内阻尼相加等于水中结构振动的总的阻尼。

4.2 水深与桩长之比d/L 影响

为了分析水深对桩基结构在水中阻尼比的影响，在结构保持不变的情况下，水深d 与桩长L 的比值依次取0.5、0.6、0.7、0.8、0.868、0.9。让结构在冲击荷载作用后进行自由振动。由此得到一系列结构横向振动的桩顶水平位移时程曲线，采用对数衰减法计算结构振动过程中的阻尼比。水体产生的阻尼比随水深变化情况如图12 所示。

从图12 中可以看出，在水深比小于0.5 时，水体引起的阻尼比较小，可忽略不计。随着水深增大，水体引起的阻尼比逐渐增加。

4.3 不同桩径的影响

保持上部结构不变的情况下，通过改变桩径来研究桩径变化对水体产生的阻尼比的影响。模型中桩径分别取1.2 m、1.8 m、2.4 m，壁厚均取22 mm。则在不同桩径下，阻尼比随水深变化情况如图13 所示。

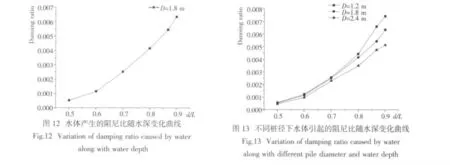
由图13 可知，在不同桩径情况下，水体产生的阻尼比均随水深增加而增大，且桩径对于水体产生的阻尼比有一定的影响。在水深比相同情况下，桩径大的结构由水体产生的阻尼比比桩径小的结构由水体产生的阻尼比小，这和文献［12］中的实验研究相吻合。港口工程中离岸深水结构桩径一般介于1.2～2.4 m、水深比一般介于0.8～0.9，从图13 可知水体引起的阻尼比介于0.003 5～0.007 5。

5 结论

水-结构的耦合振动是一个比较复杂的问题，针对现有研究的不足，并结合工程实践的需要，本文通过建立水体-桩基结构相互作用的三维有限元数值模型，分析了水体对结构自振特性及阻尼比的影响，得到一些可供工程设计参考的数据和结论：

（1）水体对桩基结构横向振动自振特性具有较明显的影响，随着水深比d/L 的增大，结构基频呈下降趋势。在水深小于桩长的50%以内时，流固耦合对基频影响较小，水深大于桩长50%以后，流固耦合对基频的影响逐渐增大。桩径较大的结构其基频受水的影响程度要大于桩径较小的结构。

（2）水体对桩柱的影响相当于附加在桩上的分布质量，当附加质量的量级与结构的质量同一量级时，流固耦合引起的基频降低幅度较大。随着上部结构质量的增加，附加质量与结构质量的比值逐渐减小，流固耦合引起的基频降低趋势减弱。

（3）对于港口工程中水深较大的桩基结构，其柔度较大，自振周期大，接近波浪等动力荷载周期。流固耦合作用引起结构基频降低，使周期进一步增大，更易诱发结构共振。因此对港口工程离岸深水桩基结构进行自振特性分析时，应考虑流固耦合作用的影响。

（4）由于水体是粘性体，结构在水中振动其阻尼比相对无水情况有所增大，水体引起的阻尼比可与结构内阻尼比线性叠加。随水深增加，水体引起的阻尼比逐渐增大。同一水深比情况下，桩径大的结构由水体产生的阻尼比比桩径小的结构由水体产生的阻尼比小。对于港口工程中离岸深水结构，由水体产生的阻尼比介于0.003 5～0.007 5，可根据桩径和水深比参照图13 进行取值。

［1］宗泽. 离岸深水码头全直桩结构分析［D］. 南京：河海大学，2007.

［2］赵石峰. 大型开敞式深水码头建设关键技术研究［D］. 大连：大连理工大学，2008.

［3］丁思远. 粘性流体对结构固有频率及阻尼的影响［J］. 郑州轻工业学院学报，1994，3（4）: 50-53.DING S Y. The effects of viscous fluids on original frequency and damping of structure［J］. Journal of Zhengzhou Institute of Light Industry，1994，9（4）:50-53.

［4］于洋，周树信. 浅水对柱体附加质量与阻尼系数的影响［J］. 大连海事大学学报，1995，21（1）: 51-55.YU Y，ZHOU S X. Added-mass and damping coefficients of a slender body under the influence of shallow water［J］. Journal of Dalian Maritime University，1995，21（1）:51-55.

［5］张悉德. 部分埋入水中悬臂圆柱体的弯曲自由振动［J］. 应用数学和力学，1982，3（4）: 537-546.ZHANG X D. Free Bending Vibration of Circular Column Partially Submerged in Water［J］. Applied Mathematics and Mechanics，1982，3（4）:537-546.

［6］张绍文，倪汉根. 水中悬臂结构振动与水动力特性研究［J］.大连理工大学学报，1996，36（3）: 329-333.ZHANG S W，NI H G. Study of hydrodynamic characteristics and vibration of cantilever structure in water［J］. Journal of Dalian University of Technology，1996，36（3）:329-333.

［7］杨吉新，秦延飞，刘素云，等. 水中结构振动特性的实验研究［J］. 武汉理工大学学报：交通科学与工程版，2010，34（6）:1 104-1 107.YANG J X，QIN Y F，LIU S Y，et al. Experiment Study on Vibration Characteristic of Sturctures in Water［J］. Journal of Wuhan University of Technology：Transportation Science & Engineering，2010，34（6）:1 104-1 107.

［8］王元战，龚薇，及春宁，等. 基于粘性流模型的筒型基础防波堤波浪力数值分析［J］. 海洋工程，2008，26（3）：38-43.WANG Y Z，GONG W，JI C N，et al. Numerical analysis of wave force on cylindrical foundation breakwater based on viscous flow model［J］. The ocean engineering，2008，26（3）:38-43.

［9］张敏. 桥墩与河水流固耦合振动分析［D］.大连：大连交通大学，2006.

［10］张文清. 悬臂管在同心套管包围的水中振动特性的研究［J］. 核科学与工程，1993，13（3）: 211-217.ZHANG W Q.Study on bibration character for a cantilever tube in water confined by concentric tube［J］.Chinese Journal of Nuclear Science and Engineering，1993，13（3）:211-217.

［11］唐友刚. 高等结构动力学［M］. 天津: 天津大学出版社，2002.

［12］M·G·哈勒姆，N·J·黑弗，L·R·伍顿. 海洋建筑物动力学［M］. 北京: 海洋出版社，1981.