政府支持企业R＆D项目中运用线性回归方法选择目标企业

杨 云，庞 宇，韩 勇

(科学技术部评估中心，北京 100081)

1 引言

线性回归方法是实证研究中最简单、最常用的一种方法。它用于确定自变量和因变量之间的关系，例如，企业销售收入与研发经费投入、科研人员数量之间的关系。通过已知的数据，按照统计学的规律，采用线性回归方法求出一个方程，就可以预测出:自变量发生改变时，因变量会有什么样的改变。

这种方法在科研管理实践有着广泛的用途。例如，在政府支持企业R＆D项目中选择目标企业时，我们可以根据企业的历年数据，考察哪一些企业的R＆D投入带来了更多的产出，从而选择这些企业作为资助对象。

2 线性回归的简化理解

根据若干组自变量和因变量数据，用数学方法就可以求出线性回归方程 (具体的方法在本文后面介绍)。例如，

Y=30.6×X+250，R=0.8，n=20

此为一元线性回归方程。其中，Y是因变量，只有X一个自变量，30.6为回归系数，R=0.8为相关系数，n=20为样本数。R和n的数值决定了所得方程是否可靠，n越大，说明观察的样本数越多，越容易接近真实情况。R越接近1，说明根据样本数据描出的坐标点越接近所得方程表示的曲线，换言之，就是方程越接近真实情况。在常见的统计学教科书中，都会给出一个相关系数表，通过查表可以得出，不同样本数对相关系数有不同的要求。例如，当 n=10时，相关系数 R=0.76460，置信度=0.01(表明有99%的概率方程是准确的);相关系数R=0.63190，置信度=0.05(表明有95%的概率方程是准确的)。通常只要做到置信度不小于0.05就可以了。

在置信度可以接受 (小于0.05)的情况下，回归系数越大，说明自变量对因变量的影响越大。回归系数为正数，表明因变量与自变量存在正相关关系。反之，则表明因变量与自变量存在负相关关系。我们通常要做的，是寻找因变量与哪些自变量存在正相关关系，哪个自变量对因变量的影响最大。

大量文献表明，R＆D投入与产出存在正相关关系。以江苏省1562家高新技术企业的研究样本为例，研发经费投入力度与技术创新绩效产出存在明显的正相关关系［1］。西安高新区2900家企业研发投入与产出的数据分析也表明，企业研发投入与产出绩效之间存在明显的正相关关系［2］。用1995—2005年中国R＆D资本存量与中国高技术产业各个产出指标进行分析，发现它与该行业专利申请受理数量、销售收入、利润和新产品销售收入等指标都存在显著的正线性相关关系［3］。用1992—2007年全国R＆D投入与产出增长的数据分析，也显示我国企业研发投入与产出增长之间存在着明显的单向因果关系［4］。

3 用简单易行的分析工具求线性回归方程

在科研管理实践中，真正运用实证方法选择目标企业的实例不多。其原因是，实证方法涉及大量的数学计算，一些人无力为之，一些人不愿为之。

线性回归是实证研究中最简单的方法之一，但是对不熟悉数学和计量经济方法的人来说，还是有些望而生畏。笔者在实际工作中，发现了两个简单易行的工具，这里特别介绍给大家:

(1)Microsoft Excel。用Microsoft Excel 2007以上版本可以做一元一次线性回归分析。在Excel表格中填入自变量和因变量数值，选择数据，插入“散点图”。双击图片，在图表工具栏中下拉选择图表类型，选择带fx标志的图表类型，就可以自动得出线性回归曲线、线性回归方程和相关系数。

(2)数学集成计算系统Forlab。数学集成计算系统Forlab是一个功能很强大的数理运算软件系统，能够解决大部分的数学计算问题。它的功能包括:全屏幕编辑制表、Forcal编程计算、函数作图、矩阵运算及数据分析、多元分析、数值计算以及建立各种数学模型等。系统界面简洁，功能实用，易于操作。

Forlab数据区和计算结果是各自独立的，数据区以表格形式进行分析，计算结果则视情况分别以文本方式或者表格的方式进行显示。数据区和结果都可以用鼠标进行任意剪切、复制、粘贴等编辑，而且可以与Excel表格进行剪切、复制、粘贴等编辑。Forlab可以免费下载。

4 运用线性回归方法选择目标企业的尝试

最近，我们协助开展了科学仪器重大专项的有关工作，科技管理部门有意在研发方面对一部分企业给予支持。我们的任务是协助选择有实力、有发展潜力的目标企业。

我们尝试用实证方法。中国高新企业数据库积累了大量的企业基本信息和经营数据资料。我们从中选择仪表行业的企业数据，第一步确定挑选的数据字段包括企业名称、年份、企业注册时间、工业总产值、主营业务收入、净利润、年末负债合计、年末资产总计、年末资产负债率、研发经费投入合计、全职科研人员数量、年末从业人员数、发明专利授权数。查询仪表企业的10年经营数据，时间跨度为2001—2010年。经过查询，找到数据比较完整的企业总共有48家。

如前所述，大量文献表明R＆D投入与产出存在正相关关系。产出主要表现为企业收入、企业利润、发明专利等。我们希望从仪表行业整体的角度，来看看R＆D投入与哪一项产出的相关关系更明显，以便找出最主要的数据项，作为我们选择企业的依据。其中，发利专利授权数只有2006到2010年期间的5年数据。为了简化问题，我们不做多元线性回归，而是做三次一元线性回归。以R＆D投入 (RD)为自变量，分别以企业收入(Re)、企业利润 (Pr)和发明专利数 (Pa)为因变量。四组数据均采用48家企业10年总额，以便了解行业的整体状况。用Microsoft Excel 2007很容易对数据进行汇总，并得出相应的线性回归方程。见图1、图2、图3，分别得出三个方程如下:

①Re=34.38×RD+25044，R2=0.566(R=0.752)，n=48

图1 研发支出 (RD)与企业收入 (Re)的相关性曲线

②Pr=1.631×RD+18187，R2=0.28(R=0.529)，n=48

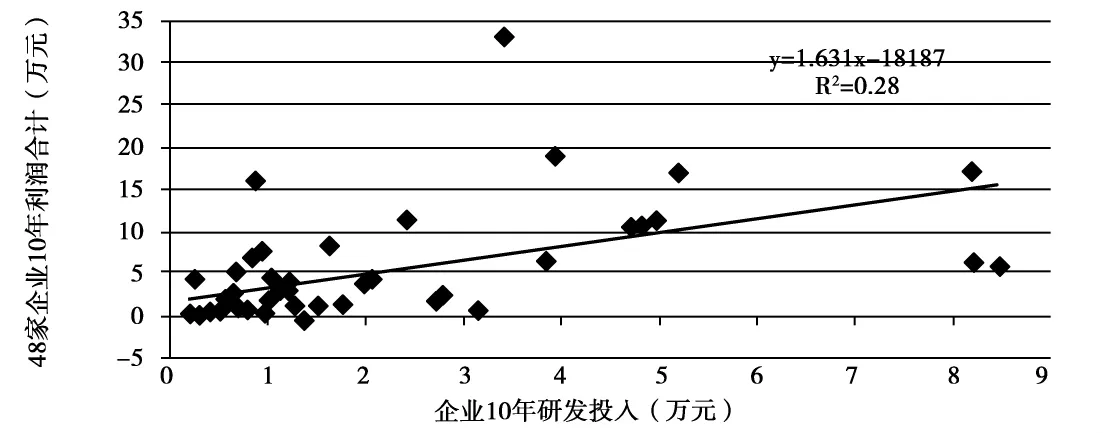
图2 研发投入 (RD)与企业利润 (Pr)的相关性曲线

③Pa=2×10－5×RD+25.73，R2=0.005(R=0.071)，n=48

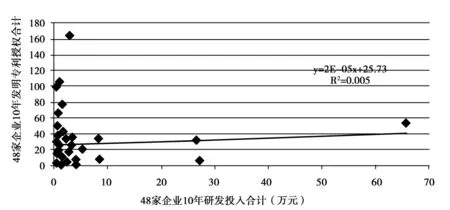
图3 研发投入 (RD)与发明专利授权数 (Pa)的相关性曲线

查阅相关系数表知道，n=48时，置信度ɑ=0.05对相关系数的要求是R不小于0.28452。由此表明，前两个回归方程都是可以置信的。企业收入、企业利润与研发投入存在正相关关系，其中，企业收入受研发投入的影响最大。发明专利授权数与研发投入的相关性不明显，大概是因为发明专利授权数只有5年数据，导致数据没有代表性。

通过以上分析，我们就确定了选择目标企业的方法:以各家企业10年的企业收入 (Rei)与研发投入 (RDi)数据为切入点，进行48次线性回归分析，分别求解每一家企业的线性回归方程。在置信度允许的前提下，选出回归系数最高的企业作为目标企业。

在企业计算过程中，由于企业在某些年份的研发投入为零，为了减少这些异常情况的干扰，我们将这些数据做剔除处理。因此，不是每家企业都是用10年数据做回归的。表1中列出n值，代表企业数据所包含的年数。根据数学上的经验，线性回归的样本数一般不宜小于5。

依次对48家企业的数据进行线性回归分析，得出回归系数值最大的前5家企业如下表，同时列出线性回归的相关系数R作为参考。

我们通过案头研究、企业访谈等方式对选出来的企业进行考察，对实证研究得出的结论给予了佐证。

贵阳新天光电科技有限公司是国家机电行业大型高新技术企业，一直被列为贵阳市、贵州省及国家重点发展的装备制造企业，在2006年还被国家统计局认定为“自主创新能力行业十强企业”。

浙江佳环电子有限公司是国家重点高新技术企业、中国环境保护产业骨干企业，产品覆盖全国30个省市自治区及远销国外。

吉林市光大电力设备有限责任公司国内电厂化学领域知名企业，是吉林省政府命名的小巨人企业，是国家人事部首批批准设立“国家博士后科研工作分站”的企业。

表1 五家企业研发投入与收入线性回归的相关系数

北京牡丹联友环保科技股份有限公司是北京中关村科技园区的高新技术企业和北京市重点扶持的环保企业。该公司的HP5000烟气在线监测设备拥有全部自主知识产权和专有技术。已有1100多套HP5000型烟气在线监测系统在北京、上海、天津等20多个省市投入运行。

爱博精电公司是国际领先的能源管理和智能测量仪表供应商，在拥有自主知识产权的产品，应用于市政、机场、石化、冶金、交通、医院、大学、数据中心、银行、国防和电力等领域。

从数据出发选择企业，然后跟定性观察相对照，这样既能做到选出优秀的企业，又能做到公平公正。

以上实践表明，线性回归这样的实证研究方法，简单、有效，不熟悉计量经济专门知识的人也可以掌握，在科研管理的实际工作可以广泛加以应用。希望给为广大同行提供参考。

［1］胡义东，仲伟俊．高新技术企业技术创新绩效影响因素的实证研究［J］．中国科技论坛，2011，(4):80－85．

［2］王育宝，吴淑娥，胡芳肖等．科技园区企业科技投入与产出绩效关系的实证分析——以西安高新区为例［J］．科技进步与对策，2010，27(7):29 －33．

［3］张小蒂，王中兴．中国R＆D投入与高技术产业研发产出的相关性分析［J］．科学学研究，2008，26(3):526－529．

［4］于成学．我国企业研发投入与产出增长关系的实证研究［J］．科技管理研究，2009，29(10):315－317．