基于亚波长二维光栅的入射角不敏感颜色滤光片研究*
2013-08-22洪亮杨陈楹沈伟东叶辉章岳光刘旭
洪亮 杨陈楹 沈伟东 叶辉 章岳光 刘旭
(浙江大学光电信息工程学系,现代光学仪器国家重点实验室,杭州 310027)
(2012年7月13日收到;2012年9月19日收到修改稿)
1 引言
具有入射角不敏感特性的颜色滤光片在传感探测、液晶显示、彩色印刷和装饰等领域具有重要的应用前景.传统的光学薄膜干涉滤光片有显著的蓝移现象,即光谱曲线会随着入射角的增大向短波方向移动,因而限制了其在大角度下的应用.近年来,随着微纳米光栅电磁理论研究的深入和微纳米加工技术的发展,研究人员提出了各种由亚波长光栅结构构建的颜色滤光片[1-5].导模共振滤光片[1,2]通过将光栅介质内的高级次泄漏模与波导模式耦合,在很小范围内引起入射光能量在反射和透射间的切换,从而得到超窄带的滤光片,然而导模共振滤光片对入射角度极为敏感,即使可以通过结构优化等手段扩展其入射角容忍度,但还是难以得到较大的入射角不敏感特性[6,7].Kanamori等[5]采用单层的亚波长光栅结构,通过在石英衬底上制备硅材料的一维亚波长光栅,得到了红、绿、蓝三色的透射颜色滤光片,但其特性会随入角度而变化.研究人员还提出了层叠的亚波长光栅结构[8-11],将两层一维或二维的亚波长光栅层叠起来,得到正入射下性能更佳的颜色滤光片.为了改善入射角不敏感特性,Cheong等[12,13]使用高折射率的硅作为二维亚波长光栅材料来实现强调制光栅,得到了s偏振光入射情况下具有较大角度不敏感特性的反射式滤光片.然而,其结构在p偏振入射的情况下,随着入射角的增大,反射率不断降低且带宽不断减少,因而在非偏振光入射的情况下随入射角增大其通带反射率会大幅下降.目前尚未见非偏振光入射下光学特性随入射角不敏感的反射滤光片的报道.
本文提出了一种基于亚波长二维光栅结构的入射角不敏感反射式滤光片.使用严格耦合波分析理论(rigorous coupled-wave analysis,RCWA)[14]进行仿真计算,详细分析了光栅周期、光栅层高度、光栅尺寸等参数变化对光栅反射光谱的影响,并验证了其在非偏振光入射情况下的入射角不敏感特性.
2 仿真模型与分析理论
本文设计的单元结构为三角柱的二维亚波长光栅,其结构如图1所示.其中t表示光栅层厚度,Λx与Λy表示光栅x和y方向的周期,a和h分别表示三角柱的底边和高.为了简化结构设计,在后续的仿真中,均有Λx=Λy且a=h.由于设计的光栅单元为三角形,沿x和y两方向的占空比是渐变的,为了方便描述,文中将占空比 f定义为a/Λx.入射介质和衬底分别为空气和熔融石英,其折射率固定为n0=1.0和ns=1.46,光栅材料采用多晶硅,其折射率与消光系数采用文献[15]的数据,节点中间的值采用线性插值得到.

图1 亚波长二维光栅的结构示意图
求解亚波长光栅的反射光谱使用的是RCWA方法.RCWA方法是通过求解麦克斯韦方程组来分析光栅结构衍射问题的方法.其求解过程可大致概括为以下几个步骤[16]:1)入射区域和透射区域,写出电场表达式并求得磁场表达式;2)光栅区域,将其介电常数分布及电磁场展开为傅里叶级数的形式,并代入麦克斯韦方程组,得到各级次的耦合波方程;3)在边界处运用电磁场边界条件,得到各级次衍射波的振幅及衍射效率.由于在理论推导过程中不存在近似,因此RCWA方法是一种精确求解麦克斯韦方程组的方法.在实际计算中,受限于计算机的性能和计算时间,只能考虑有限级次的衍射级.在仿真中,x和y方向上保留衍射级数都定为5.
我们使用RCWA算法模拟分析了设计结构在s和p偏振光入射情况下的反射光谱及入射角不敏感特性,模拟的波长范围为380 nm到780 nm的可见光波段,并使用时域有限差分算法(FDTD)对最终结果进行了验证.采用RCWA算法分析了不同光栅周期、光栅厚度值、光栅占空比等结构参数对反射光谱及非偏振光入射角不敏感特性的影响.
3 模拟结果与讨论
3.1 设计结构的模拟结果
设计的二维光栅滤光片的结构参数为Λx=Λy=120 nm,a=h=100 nm,t=100 nm,其反射光谱与入射角关系如图2所示.设计的光栅滤光片的中心波长为424 nm,其带宽约45 nm,最大反射率为56%.图2(a),2(b)分别为s和p偏振光入射的情况.随着入射角的增大,各波长的反射率在s偏振光入射时均有所增加,而p偏振光入射时则有所减小,中心波长位置则几乎没有改变.将s和p偏振光的反射率平均,得到在非偏振光入射下的反射光谱.从图2(c)可以看出,当入射角从0°增加到40°时,反射光谱几乎没有变化,而入射角进一步增加到60°时,其反射光中心波长向长波方向移动了约6 nm,反射率下降了6%.由反射光谱计算出CIE1931色品图上的位置如图2(d)所示,考察的入射角从0°至60°,间隔10°.可见设计滤光片的颜色为紫色,在40°范围内颜色变化范围很小.由此可见,设计的基于二维亚波长光栅反射式滤光片,具有良好的入射角不敏感特性.在非偏振光入射的情况下,入射角从0°增加到60°,都可以保持其反射带位置和反射率基本不变.
亚波长二维光栅的光学特性与光栅周期、光栅层厚度、光栅尺寸大小等因素相关,下面将分别分析这些因素对反射光谱及入射角不敏感特性的具体影响.
3.2 光栅周期对反射光谱及入射角不敏感特性的影响
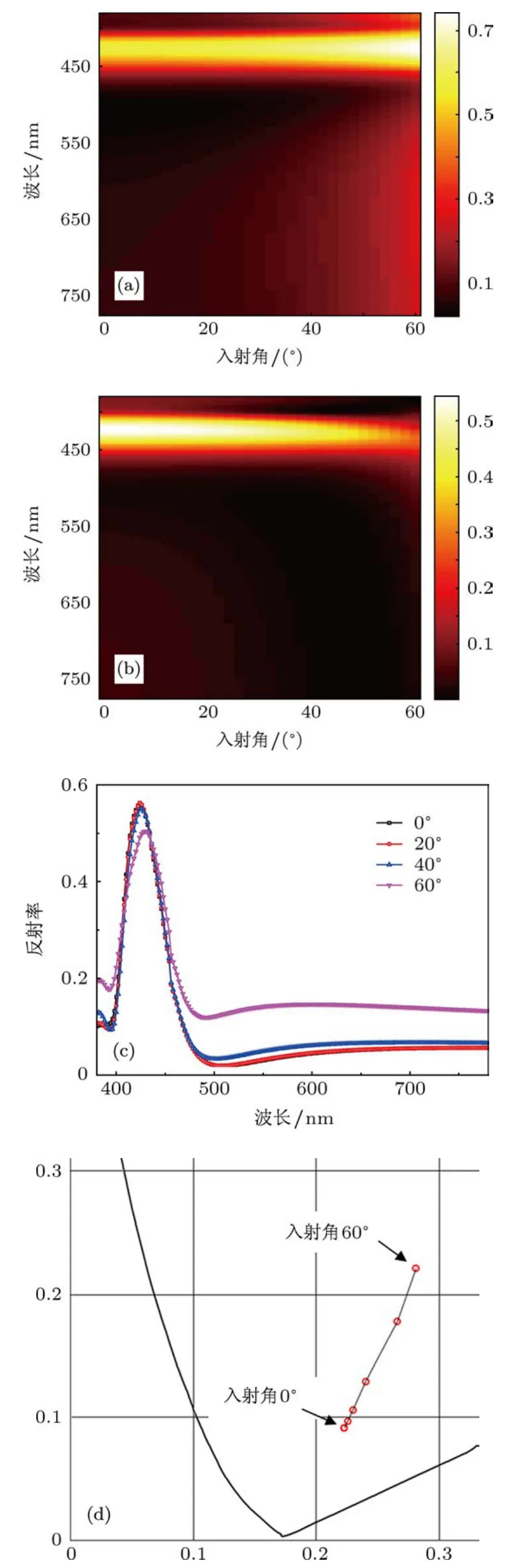
图2 亚波长二维光栅光学特性的模拟结果 (a)s偏振光入射;(b)p偏振光入射;(c)非偏振光入射下的反射率曲线;(d)设计滤光片的色坐标位置随角度变化示意
首先考察的是光栅周期.初始结构设定a=h=0.1µm,t=0.1µm,Λx与Λy的变化范围从0.1µm到0.2µm,步长0.01µm.图3展示了光栅周期对反射光谱及入射角度敏感性的影响.非偏振光正入射的反射光谱图如图3(a)所示,光栅周期主要影响的是峰值反射率,而对反射光谱形状、峰值位置和带宽的影响较小.考察其入射角敏感性时,由于反射带带宽在不同入射角下的变化不大,因而主要对比了反射率峰值和峰值位置这两个参数.正入射和入射角为45°时光栅周期对反射率峰值和峰值位置的影响如图3(b)所示.正入射时,反射率先增大后逐渐递减,在Λx=Λy=0.13µm时达到最大反射率56.6%,而反射率峰值位置变化不大.对比两种入射角的情况,当光栅周期大于0.12µm时,两种入射角下反射率峰值和峰值位置的差值开始增大,入射角不敏感特性减弱.

图3 非偏振光入射下光栅反射光谱与光栅周期的关系(a)正入射时不同周期的反射光谱;(b)入射角为0°和45°时反射率峰值和峰值位置随光栅周期的变化情况
3.3 光栅层厚度对反射光谱及入射角不敏感特性的影响
图4考察光栅层厚度对反射光谱的影响.初始结构设定a=h=0.1µm,Λx=Λy=0.12µm,t的变化范围从0.05µm到0.25µm,步长0.01µm.从图4(a)可以看出,非偏振光正入射时,随着厚度的增加,反射带带宽逐渐增加,峰值位置向长波方向移动,而反射峰值先增大再减小.当厚度增大到0.16µm时其反射光谱特性已经很差.图4(b)为正入射和45°入射角时反射光谱峰值和峰值位置与光栅层厚度的关系图.两种入射角下反射率峰值的差异并不大,反射率峰值的最大值出现在光栅层厚度为0.1µm附近,此后的反射率峰值开始迅速下降,当厚度大于0.14µm后,其反射率峰值降至小于30%.至于反射率峰值位置,在光栅层厚度小于0.15µm时,两个入射角下反射率峰值和峰值位置的差值并不大,随着厚度的增加,反射率峰值位置向长波方向移动,两者基本成线性关系.

图4 非偏振光入射下光栅反射光谱与光栅层厚度的关系(a)正入射时不同光栅层厚度的光谱;(b)入射角为0°和45°时反射率峰值和峰值位置随光栅层厚度的变化情况
3.4 固定占空比后光栅结构尺寸对反射光谱及入射角不敏感特性的影响
光栅结构的尺寸大小同样对其反射光谱特性有影响,因此尝试等比例放大或缩小光栅结构,考察反射光谱以及入射角不敏感特性的变化情况.根据前面讨论的结果,当a=h=0.1µm,Λx=Λy=0.12µm时可以获得较高的反射率和入射角不敏感特性,因此将f固定为0.1/0.12,光栅层厚度t固定为0.1µm,改变三角形的底边长度a从0.05µm到0.25µm,步长0.01µm,观察不同入射角度情况下的反射光谱峰值位置和带宽的变化.从图5(a)中可以看出,非偏振光正入射和45°角入射时,反射带的位置基本未变,而尺寸较大结构的反射带反射率有显著的下降.此外,图5(a)中a为0.23µm,入射角为45°情况下的光谱在620 nm附近出现了反射率突变.这是因为此时入射光波长约为光栅周期的一倍到两倍之间,使得光栅处于共振区而发生瑞利伍德反常[4,17,18],造成特定波长附近的反射率出现突变.因此结合考虑入射角不敏感特性,需要在通带附近避开光栅共振区.图5(b)展示了0°和45°入射时反射光谱峰值和峰值位置随三角形底边长度的变化关系.当a大于0.14µm后,两种入射角反射率峰值的差值迅速增大,且在a继续增大到大于0.2µm后,瑞利伍德反常会对光谱形状有进一步影响.因此,在固定占空比为0.1/0.12的情况下,为保持较好的入射角不敏感特性,三角形底边长度可在小于0.14µm的范围内调节以改变反射率峰值波长位置,反射率峰值位置的变化范围可从400 nm至480 nm.
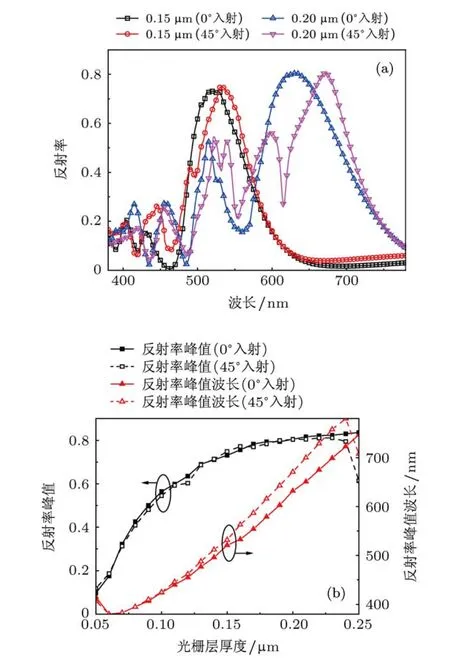
图6 非偏振光入射下,固定光栅层厚度、三角形底边和光栅周期的比例后的反射光谱与光栅层厚度的关系 (a)正入射与45°入射时两种光栅层厚度的反射光谱;(b)入射角为0°和45°时反射率峰值和反射率峰值位置随光栅层厚度的变化情况
为了进一步增加峰值波长位置的可调节范围,还可以固定光栅层厚度t与三角形底边a以及光栅周期Λ的比值,同比例改变这些结构参数.仿真中固定 t:a:Λ=0.1:0.1:0.12,t的变化范围为0.05µm至0.25µm,步长0.01µm.图6(a)为两种大小的结构在非偏振光入射下的反射光谱图.对比光栅层厚为0.15µm和0.2µm的正入射光谱图可以发现,随着结构尺寸的增大,光谱在短波方向上会出现次级反射峰而影响其特性.此外,在45°角入射t为0.2µm的反射光谱中,同样观察到了反射率突变现象,使得两种入射角的光谱曲线形状差异较大,而t为0.15µm时,两种入射角的光谱曲线形状差异较小.图6(b)对比了0°和45°入射时反射光谱峰值和峰值位置随结构尺寸大小的变化关系.可见两种入射角的反射率峰值差异不大,而在光栅层厚度大于0.15µm后,两种入射角的反射率峰值位置差异迅速增大,加之大结构尺寸在大入射角下会发生反射率突变反常,因此为保持较好的入射角不敏感特性,在固定光栅层厚度和占空比的比例为0.1:0.1/0.12时,光栅层厚度需小于0.15µm,此时反射率峰值位置的调节范围为400 nm至520 nm.
综上所述,对于设计的亚波长二维光栅结构,光栅周期和光栅层厚度均对反射率大小有影响,通过调节光栅层厚度,可以一定范围内改变峰值波长位置.此外,在固定占空比以及占空比和光栅层厚度的比例时,可以更大范围地调节反射光谱的峰值波长位置.
4 结论
本文基于亚波长二维光栅结构,提出了光栅单元结构为三角柱的反射式颜色滤光片.仿真使用严格耦合波分析算法,设计优化了中心波长424 nm,峰值反射率为56%,带宽约45 nm的反射式滤光片.仿真结果表明,设计的滤光片在非偏振光入射的情况下,反射光谱在入射角高达60°时仍没有显著改变,表现出显著的入射角不敏感特性.本文还分析了光栅周期、光栅层厚度等参数对其反射光谱的影响,这些因素主要影响反射光谱的反射率峰值和中心波长,因此可以通过在一定范围内调节这些参数,得到不同中心波长的滤光片,调节范围可从400 nm至520 nm.
[1]Magnusson R,Wang S S 1992 Appl.Phys.Lett.61 1022
[2]Ma J Y,Liu S J,Wei Z Y,Xu C,Jin Y X,Zhao Y A,Shao J D,Fan Z X 2008 Acta Phys.Sin.57 827(in Chinese)[麻健勇,刘世杰,魏朝阳,许程,晋云霞,赵元安,邵建达,范正修2008物理学报57 827]
[3]Chen Q,Cumming D R S 2010 Opt.Exp.18 14056
[4]Zhao H J,Yang S L,Zhang D,Liang K Y,Cheng Z F,Shi D P 2009 Acta Phys.Sin.58 6236(in Chinese)[赵华君,杨守良,张东,梁康有,程正富,石东平2009物理学报58 6236]
[5]Kanamori Y,Shimono M,Hane K 2006 IEEE Photon.Technol.Lett.18 2126
[6]Li C G,Gao Y H,Xu X S 2012 Chin.Phys.Lett.29 034202
[7]Lemarchand F,Sentenac A,Giovannini H 1998 Opt.Lett.23 1149
[8]Yoon Y T,Lee H S,Lee S S,Kim S H,Park J D,Lee K D 2008 Opt.Exp.16 2374
[9]Lee H S,Yoon Y T,Lee S S,Kim S H,Lee K D 2007 Opt.Exp.15 15457
[10]Ye Y,Zhou Y,Zhang H,Chen L S 2011 Appl.Opt.50 1356
[11]Ye Y,Zhang H,Zhou Y,Chen L S 2010 Opt.Commun.283 613
[12]Cheong B H,Prudnikov O N,Cho E,Kim H S,Yu J,Cho Y S,Choi H Y,Shin S T 2009 Appl.Phys.Lett.94 213104
[13]Cho E H,Kim H S,Cheong B H,Prudnikov O,Xianyua W,Sohn J S,Ma D J,Choi H Y,Park N C,Park Y P 2009 Opt.Exp.17 8621
[14]Moharam M G,Gaylord T K 1981 J.Opt.Soc.Am.71 811
[15]Palik E D 1985 Handbook of Optical Constants of Solids(Vol.1)(New York:Academic)p563
[16]Moharam M G,Grann E B,Pommet D A,Gaylord T K 1995 J.Opt.Soc.Am.12 1068
[17]Fu Z P,Lin F,Zhu X 2011 Acta Phys.Sin.60 114213(in Chinese)[傅正平,林峰,朱星2011物理学报60 114213]
[18]Hessel A,Oliner A A 1965 Appl.Opt.4 1275
