自由曲面数控加工的实时自适应进给速度规划算法

董靖川，王太勇，丁彦玉，李 勃，刘 喆

（1. 天津大学 电气与自动化工程学院，天津 300072；2. 天津大学 机构理论与装备设计教育部重点实验室，天津300072；3. 天津大学 机械工程学院，天津，300072）

0 引言

进给速度规划对数控机床的加工效率、轮廓精度、振动和表面质量等方面有重要影响。对于自由曲面的加工，CAM软件生成的程序包含了大量的由小线段组成的刀具路径。数控系统需要在机床性能的约束条件下对进给速度曲线进行优化，以减少加工时间并获得平滑的进给运动。

为了实现小线段程序的高速平滑加工，在数控系统中引入了前瞻算法。前瞻算法提前预读若干程序段，并通过对预读程序段的分析实施加减速处理。Han等人[1]引入了预读缓冲区实现对小线段的速度规划。Hu等人[2]讨论了小线段转角的约束条件，并对前瞻段数和时间的关系进行了仿真。Luo等人[3]发表一种通过双向链表数据结构实现的通过速度规划算法。Ye等人[4,5]对小线段几何特征进行分类，引入了包含多个小线段的规划元。但是该方法中要求规划元内小线段数目基本相等，而且需要根据经验指定。

小线段路径在转角位置具有方向不连续性。为了提高加工速度，降低冲击，很多学者应用曲线拟合或插值的方法修改程序中的加工路径以提高连续性[6～8]。但曲线构造、速度规划和插补的方法需要的运算量非常大，而且会产生一定的误差。实际上，在生成自由曲面加工程序时，由于原始刀具路径本身是连续曲线，可以通过提高CAM软件的直线拟合精度减小生成的程序中相邻小线段间的方向变化。但在复杂曲面加工中，刀具路径的曲率变化范围很大，在高曲率位置如果以高速进给会产生很大的冲击，需要进行适当控制[10]。同时，在不同曲面相交的位置刀具进给方向也会发生突变，需要预先检测并处理。

本文针对自由曲面数控加工的小线段程序，提出了一种自适应进给速度规划算法。通过分析小线段间几何关系对曲率进行估计，在此基础上实施进给速度调整。同时检测进给速度具有较大突变的转角位置，进行速度限制。在前瞻处理中采用了具有限制加加速度的7段加减速曲线，给出了不同情况下的规划解。在该算法中开发了目标速度滤波器，以减小进给速度波动，并降低速度规划单元的数量，减少实时运算负担。最后，通过仿真和实际加工测试验证了本文算法的有效性。

1 自适应进给速度调整

1.1 加工路径曲率估计

在自由曲面的高速加工中，如果采用恒定的进给速度加工，那么在到达刀具路径曲线上大曲率的位置时将产生极大的加速度冲击，导致轮廓误差增大和机床结构振动。为了达到平稳的加工效果，数控系统需要在大曲率位置自动减速，降低法向加速度。在三维空间中，对于解析式已知的参数曲线，曲率κ可由下式确定：

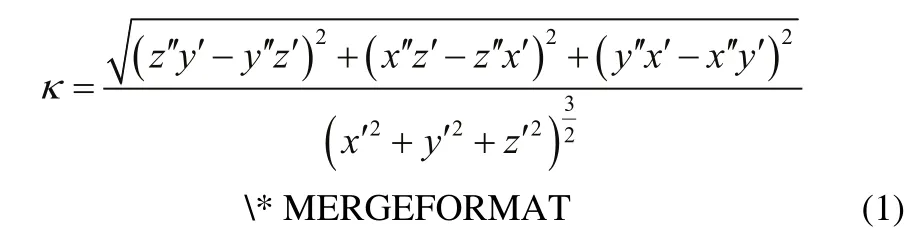
然而，对于由微小线段组成的加工路径，无法获得曲率的解析表达式，因此只能根据线段间的几何关系对曲率进行估算。

首先考虑对于圆的等弦高误差小线段逼近，如图1所示。其中，φ为两个小线段间的夹角，S为小线段长度，则可求得半径R为：

注意到在生成自由曲面的数控加工程序时，为了减少小线段的数目，CAM软件同样会采取等弦高误差的方法用小线段生成加工路径。可以根据小线段的长度及线段间的夹角构造一个近似曲率圆ˆC，如图2所示，并用其半径作为曲率半径的估计。假设加工路径上某个小线段的长度为S，该线段与上一线段间的夹角为φ，则曲率半径估计值ˆρ为：

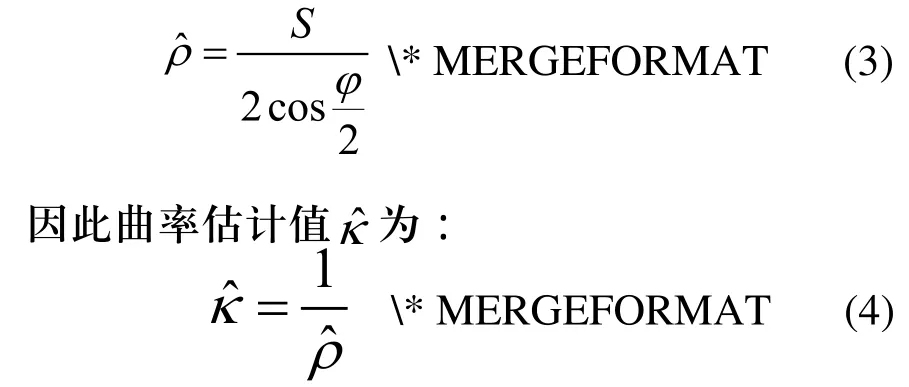
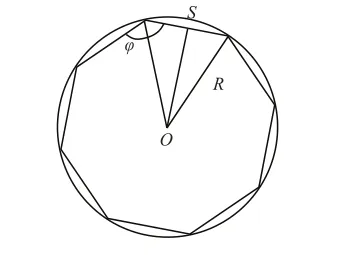
图1 圆的等弦高误差小线段逼近

图2 小线段加工路径的曲率半径估计

按照式和估计曲率时，需要进行耗时的三角函数计算。在实时速度规划中，可以用以下方法避免三角函数计算。如图3所示，假设相邻两个小线段的单位方向向量分别为1e和2e，则：

单位方向向量e1和e1还可以进一步用于插补计算。

图3 用向量关系求解

1.2 进给速度调整

若刀具路径上某一点的曲率为κ，进给速度为v，则该点的法向加速度nA为：

假设加工过程中允许的最大法向加速度为Anmax，曲率半径估计值为κˆ，由式可知进给速度v应满足：

对于刀具路径上一个小线段，假设其编程进给速度为pv，则其目标运行速度tv可设置为：

另外，如图3所示，在加工路径的上两个小线段的夹角位置，由于有速度方向的突变，可能造成冲击。在对连续曲面加工时，一般相邻小线段间夹角接近180°，冲击较小。但在刀具路径不连续的地方，例如两个曲面的相交位置，则可能造成较大冲击。因此必须限制速度突变。设伺服系统允许的最大突变为maxvΔ，则转角处进给速度cv应满足：

2 前瞻速度规划

2.1 限制加加速的加减速方法

对于运动路径上的每一个速度规划单元（简称规划元），给定其运动距离、起始速度、目标速度和结束速度，为了获得平滑的进给运动，需要应用适合的加减速方法得到其速度规划曲线。限制加加速度的加减速方法具有连续的梯形加速度曲线，减少了对结构的冲击。完整的加减速曲线包含7段[9]，如图4所示。图中，t，S，v，A，J分别表示时间，位移，速度，加速度和加加速度。在每个段内的运动方程为

根据机床特性，可以设定最大加加速度J和最大加速度Amax，则最大加加速时间Tj为:

在对小线段路径进行速度规划时，在长度较短或速度变化较小的情况下，加减速曲线可能少于7段。速度规划需要确定加减速曲线包含哪些阶段，并确定各阶段的运行时间。给定规划元长度S，起始速度vs，目标运行速度vt和目标结束速度vet，通过位移方程和速度方程可解出各段运行时间，具体规划算法如下：

图4 完整的限制加加速度加减速曲线

1）计算临界距离1cS

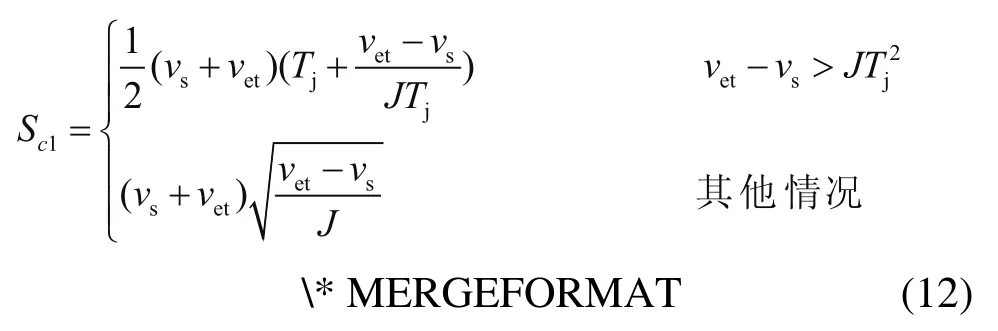
4）计算临界距离c4S

6）计算临界距离c5S

在求解某些规划结果时需要解高次多项式方程，可以采用Newton-Raphson迭代方法求得数值解，其中迭代初始值可设为

2.2 前瞻速度规划

在速度规划中，为了减少不必要的加减速，缩短加工时间，希望每个规划元的目标结束速度vet尽量大。在实时前瞻速度规划中，控制器通过提前预读多个规划元确定当前规划元的 vet。假设前瞻缓冲区内已预读了N个规划元，其中第k个规划元的长度和目标速度分别为 S (k)和 vt(k)，由式确定的第 k -1个和第k个规划元间的转接点速度限制为 vc(k - 1 )，设 vme(N)=0，则以第N段到第1段的顺序依次应用以下反向速度规划得到 vet。

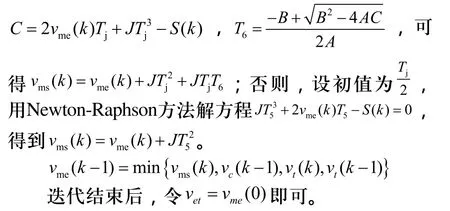
2.3 目标速度滤波器

由前瞻算法原理可知，速度元的数量决定了速度规划的实时计算量和加减速的次数。在加工小线段程序时，如果将每个小线段视为一个规划元，则需要大量实时运算，同时加减速限制在每个小线段内部，造成过多加减速。为此，本文提出了目标速度滤波器算法，以减少规划元的数量。假设第k段小线段的目标运行速度为 vtin(k)，则对应的滤波器输出 vtout(k)为

式中a为滤波器参数，取值范围[0,1)。目标速度滤波器的作用是，在目标速度变化较小时，延迟目标速度的变化，使相邻的小线段尽可能以相同的目标进给速度运行，如图5所示。

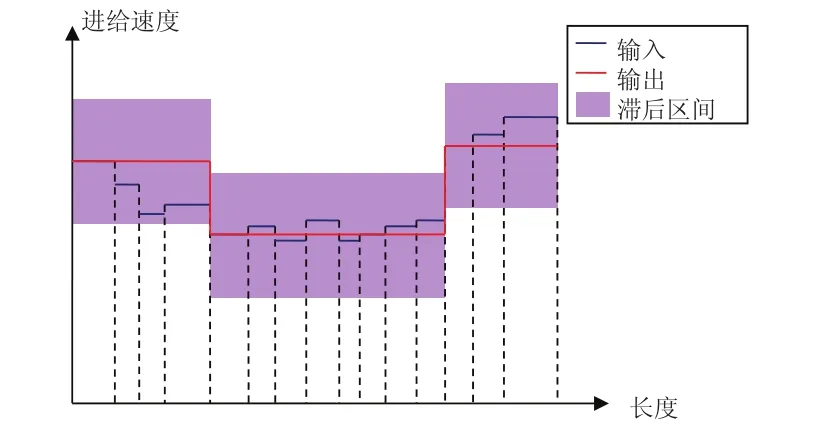
图5 目标速度滤波

若第k段和第 k + 1 段的转角限制速度为 vc(k)，则对于满足 vtout(k)= vtout(k + 1 )且的相邻两个小线段可以合并到一个规划元。通过反复执行合并，一个规划元可以包含多个微小线段。可见，目标速度滤波器减少了规划元数量，提高了加工效率。

3 实验测试

首先，在matlab软件中验证本文提出的实时自适应进给速度规划算法的有效性，测试轨迹如图6所示。该平面图形由1498条小线段构成。根据本文算法获得的曲率估计如图7所示。轨迹规划中编程进给速度为1000mm/min，前瞻规划缓冲区大小为10个规划元，允许的最大速度突变为60mm/s，最大法向加速度为50mm/s2，最大加加速度为50000mm/s3，最大加速度为2500mm/s2，滤波器参数为0.3。在未开启目标速度滤波器和开启目标速度滤波器的情况下，规划结果分别如图8和图9所示。可见，开始目标速度滤波器后，速度波动明显减少，运动轨迹更加平滑，总体运行时间也更少。同时可以看出，进给速度在尖角处和高曲率位置处自动下降，防止产生冲击，实现了自适应调整。

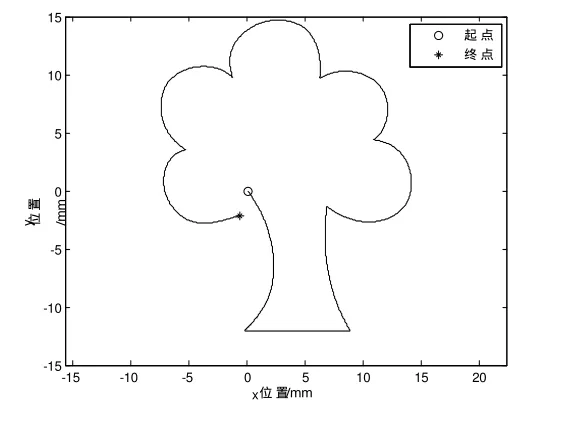
图6 平面测试刀具路径轨迹

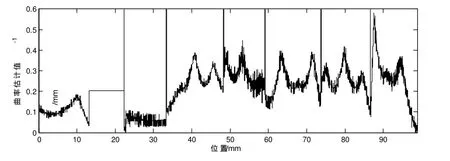
图7 平面测试刀具轨迹曲率估计

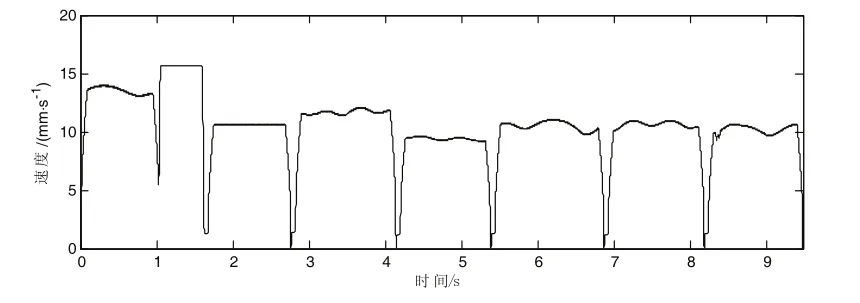
图8 未开启目标速度滤波器的规划结果

图9 开启目标速度滤波器的规划结果

为了验证实际加工自由曲面零件时的效果，在自行开发的运动控制卡上实现了本文的算法。该运动控制卡基于ARM处理器和FPGA芯片，其实物如图10所示。实际加工在一台加工中心上进行。测试加工程序为三轴联动曲面铣削，包含大量小线段，其曲率估计结果如图11所示。由于测试程序的进给方向与X轴呈45度夹角，因此看以看出曲率分布并不对称。测试时编程进给速度为2000mm/min，前瞻规划缓冲区大小为100个规划元，允许的最大速度突变为60mm/s，最大法向加速度为1000mm/s2，最大加加速度为10000mm/s3，最大加速度为500mm/s2，滤波器参数为0.3。在加工过程中切削进给平稳，没有振动现象，实际加工效果如图12所示。

图10 运动控制卡实物

图11 曲面铣削刀具路径的曲率估计结果

图12 测试加工的零件

4 结论

本文针对自由曲面的小线段程序加工问题提出了一种实时自适应进给速度规划算法。该算法能够对加工路径的曲率进行估计，并在高曲率位置和大速度突变位置自动实施减速，实现了自适应进给速度调整。通过限制加加速的前瞻速度规划处理实现了平滑的进给速度曲线。目标速度滤波器的应用减少了规划元数量，降低了实时规划运算量。仿真和实际加工测试验证了本文算法的可行性。与传统方法相比，本文方法不但能够实现基于曲率估计的自适应平滑速度规划，而且有效降低了小线段程序的前瞻处理运算量，有利于实现高性能数控加工。

[1] G-C Han, D-I. Kim, H-G. Kim, K. Nam, B-K. Choi, S-K.Kim, A high speed machining algorithm for CNC machine tools, 25th Annual Conference of the IEEE Industrial Electronics (1999) 1493-1497.

[2] J. Hu, L. Xiao, Y. Wang, Z. Wu, An optimal feedrate model and solution algorithm for a high-speed machine of small line blocks with look-ahead, The International Journal of Advanced Manufacturing Technology 28 (2006)930-935.

[3] F. Luo, Y-F. Zhou, J. Yin, A universal velocity profile generation approach for high-speed machining of small line segments with look-ahead, The International Journal of Advanced Manufacturing Technology 35 (2007) 505-518.

[4] P. Ye, C. Shi, K. Yang, Q. Lv, Interpolation of continuous micro line segment trajectories based on look-ahead algorithm in high-speed machining, The International Journal of Advanced Manufacturing Technology 37 (2008)881-897.

[5] C. Shi, P. Ye, The look-ahead function-based interpolation algorithm for continuous micro-line trajectories, The International Journal of Advanced Manufacturing Technology 54 (2011) 649-668.

[6] H. Zhao, L. Zhu, H. Ding, A real-time look-ahead interpolation methodology with curvature-continuous B-spline transition scheme for CNC machining of short line segments, International Journal of Machine Tools and Manufacture 65 (2013) 88-98.

[7] J-B. Wang, H-T. Yau, Real-time NURBS interpolator:application to short linear segments, The International Journal of Advanced Manufacturing Technology 41 (2009)1169-1185.

[8] K. Erkorkmaz, C-H. Yeung, Y. Altintas, Virtual CNC system. Part II. High speed contouring application,International Journal of Machine Tools and Manufacture 46 (2006) 1124-1138.

[9] K. Erkorkmaz, Y. Altintas, High speed CNC system design. Part I: jerk limited trajectory generation and quintic spline interpolation, International Journal of Machine Tools and Manufacture 41 (2001) 1323-1345.

[10] J.R. Conway, A.L. Darling, C.A. Ernesto, R.T. Farouki,C.A. Palomares, Experimental study of contouring accuracy for CNC machines executing curved paths with constant and curvature-dependent feedrates, Robotics and Computer-Integrated Manufacturing 29 (2013) 357-369.