随机共振信号恢复研究

张 攀，王太勇，井路阳，张 莹

(天津大学 装备设计与制造技术天津市重点实验室，天津 300072)

0 引言

自1981年Benzi[1]等人研究古气象冰川问题时提出随机共振（SR）概念以来，有关随机共振理论、实验和模型的研究[2]已成为二十多年来非线性科学研究的一个热点。在信号处理领域，随机共振可用来提取有效信号的特征频率，因此在微弱信息的检测、放大、传输等方面具有独特的优势。但同时，由于系统对周期信号的响应输出畸变为含高频成分的矩形（或梯形）波，给非方波周期信号的后续处理带来了诸多不便。

文献[3]实现了对双稳随机共振系统波形失真输出的恢复。但由于其驱动信号仅限为正弦信号，因此对于非正弦信号(特别是非周期信号)驱动的随机共振系统的恢复具有一定的局限性。能否对于工程实际处理中普遍遇到的被噪声污染的采样信号进行有效的恢复，是本文的出发点和主旨所在。

本文以含噪信号为处理对象，提出了基于信号分类的随机共振恢复方法，既对类正弦信号和类脉冲信号，分别选择级联双稳随机共振和单稳随机共振提取被噪声污染的信息，然后求取参数可调或者参数固定的恢复系统对随机共振输出的响应，从而实现工程中对含噪信号的特征提取。

1 系统化的随机共振恢复方法

随机共振现象反映了噪声和信号在非线性条件下表现出来的协同效应。事实证明，在双稳系统的阱内随机共振[4]中，噪声也会对系统行为产生积极的影响[5]。从这种意义上说，双稳系统是否处于随机共振状态，并不是以发生阱间跃迁为标志，而是看噪声是否对系统输出产生了有利的影响，这种影响既发生在阱间，也发生在阱内。因此，本文中我们称双稳系统中没有发生阱间跃迁的情况为单稳随机共振，有阱间跃迁发生时称为双稳随机共振。

文献[3]中对于正弦信号驱动下的双稳系统采用了级联双稳随机系统和参数调节的恢复系统。由于恢复方法的选择与信号特性相关，对于工程实际处理中普遍遇到的被噪声污染的采样信号,本文提出了基于信号分类的随机共振恢复方法。首先对待处理信号进行初步的分析。如果信号中包含有限几个周期成分，并且这几个成分集中于某一频段，其时域波形表现为较平滑的曲线，不含阶跃成分，我们定义这类信号为类正弦信号，采用级联双稳随机共振和参数调节的恢复系统对有效的时域波形进行恢复。如果信号包含较多或者无限多的周期成分，覆盖很宽的频域范围，其时域波形中含有脉冲的信号形式，我们定义这类信号为类脉冲信号，采用单稳随机共振和参数固定的恢复系统实现波形的恢复。操作流程如图1所示。

图1 系统化的随机共振恢复方法

需要说明的是，该分类方法对于信号是否是周期信号没有限制。下面我们将就两种方法的分别进行讨论。

2 类正弦信号的恢复方法

在外界驱动力 s(t)和由双稳系统势函数U(x) = - 1 /2a x2+ 1 /4bx4决定的能量势场的作用下，过阻尼的布朗粒子其运动满足朗之万方程：

变量上方的“•”表示对时间t求导。典型的随机共振模型中，驱动信号 s (t) = A s in(2π f0t)， n (t)是强度为D的高斯白噪声。

在绝热近似条件下[2]，粒子在 U (x)中的运动轨迹近似满足：

可见，粒子的运动轨迹 ()xt不再严格遵循 ()st的时间历程，对此，文献[3]给出恢复公式：

对于类正弦信号的恢复我们可以采用文献[3]中提出了级联双稳随机共振[6]与参数调节的恢复系统，但其对于恢复系统参数的调节并没有做具体的研究。本文将在其基础上首先研究利用级联双稳随机共振和参数调节的恢复系统中参数的选取问题。具体操作为[7]：

1）将含噪信号 s(t) + n (t)送入级联双稳系统，调节系统参数a、b和二次采样频率fsr，使得双稳系统输出达到随机共振状态。其中，两级双稳系统参数相同，输出分别为 x(t)和 y (t)。

在信号处理中，经过A/D转换，连续的时间历程 ()xt和 ()yt被离散为序列：

其中，N为采样点数。

于是，条件(5)变为对任意的01iN≤≤-满足：

带入上式，仍然成立。注意到方程(7)中分母不能为零，根据文献[3]的分析，要求 xi以及 yi的取值不包括双稳系统的拐点。在绝热近似条件下，粒子经过系统拐点时会发生极快的跃迁，所以我们在计算样本均值时应该去掉阱间跃迁的部分，即分别计算系统输出在正、负势阱中的样本均值。由于跃迁运动是对称的，两个势阱中样本均值的绝对值相等，分别定义为。于是，最优的恢复参数满足

我们仍取文献[3]中的参数：正弦信号频率f0= 0 .01Hz，幅值 A = 0 .3，噪声强度 D = 0 .28，系统参数 a = b = 1 ，采样频率 fs= 5 Hz，考察的点数为200～1200。根据文献[3]，在这组参数下可以使系统输出产生随机共振。通过计算，得到= 0 .787，= 1 .325。根据级联双稳随机共振的理论[8]，无论是第一级输出 x(t)还是第二级输出y(t)，都受到残余噪声的影响，因此样本均值和也带有一定的随机性。考察方程(9)，调节常数项a~比调节二次项系数容易避开这一随机性的影响。所以通常我们固定= 1，而只讨论恢复系统线性项系数。

文献3中描述的正是在这组参数取值下的恢复波形，可以有效的实现信号的恢复。

因此，我们可以提出“类正弦信号”的恢复方法，具体恢复过程如图2所示。

图2 “类正弦信号”的恢复方法

3 类脉冲信号的恢复方法

对于振动测试常见到周期或者非周期冲击信号，时间ε越小，对应的频谱范围越广。这种特性决定了一旦信号中含有脉冲形式，就很容易被噪声干扰。图3中的时间历程含有三个高度为1的脉冲，脉冲位置随机。

添加强度 0.1D= 的白噪声后，我们得到了图4(a)所示的混合信号，显然，我们无法从时域波形中提取到任何关于脉冲的信息，从频谱看，有效的信息也被噪声湮没，如图4(b)所示。

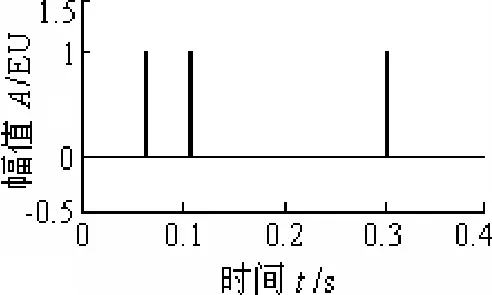
图3 随机脉冲序列的时域波形

图4 含噪脉冲序列的时域波形与频谱

考虑到双稳系统可以改变信号谱图的能量分布，使得响应信号的频谱呈现罗伦兹分布的特性，而恢复系统在一定程度上可以恢复被放大或缩小的幅值，我们采用随机共振的信号恢复方法对图4(a)中的含噪信号进行处理，取双稳系统参数，二次采样频率 fsr= 1 2Hz ，我们得到图5(a)中的随机共振输出。

由图5(a)可以看出，在上述参数下，系统行为受单阱调制，输出始终为正，此时系统处于单稳随机共振状态。这里，我们有意避开双稳共振状态，是由于一方面噪声强度比较小，单稳随机共振也可以使系统输出达到一个较为理想的状态；同时从时域看，对于非周期的脉冲序列，我们很难衡量何时为最佳的双稳共振状态，以指导参数的调节方向。

为了恢复得到脉冲的准确位置和大小，我们采用参数固定的恢复系统，即直接利用恢复公式(3)。选择恢复参数a a=~ 和b b=~ ，得到图5(b)所示的结果，可以发现脉冲的位置和高度都得到了较为精确的提取。考虑到重复性可作为判定实验结果是否有效的标准之一，我们提出了类脉冲信号的恢复方法，如图6所示。

图5 含噪脉冲序列的随机共振波形恢复

图6 “类脉冲信号”的恢复方法

4 实验验证

4.1 仿真实验一

对于单自由度振动系统，加上阻尼装置后，图7所示，其质点位移 ()xt可表示为：

上式称为有阻尼的自由振动方程，将其作为我们的目标信号。该信号是一个瞬变非周期信号，它不是一个等幅的简谐振动，其幅值按指数衰减。由于测试设备、环境等带来的干扰，采集到的信号含有大量的噪声。

图7 单自由度振动系统

图8 振动衰减信号的恢复结果

对于含噪待处理信号图8(a)，我们采用类正弦信号的恢复方法，选择参数系统为 a = b = 1 以及二次采样频率 fsr= 4 Hz[9]，得到级联双稳输出。求解样本均值，代回到方程（9）中，得到恢复参数组合 a~ = 1.68和 b~ = 1。对于图8(b)的恢复结果，经过合理的线性插值、拟合[10]等后处理，最终得到图8(c)所示的时域波形。可以清楚地看出原始信号的时域特征，判定可知恢复结果与目标信号即振动衰减信号相符，并可以计算所测结构的特征参数。

4.2 实验二

图9记录的是金属切削过程的振动信号，工程背景参见文献[6]。通过对实验背景的初步判断，我们知道，当刀具切削到棒料工件的硬点时，将产生周期性的脉冲冲击，其频率为机床主轴转频，这里将待识别的目标信号归入类脉冲信号，采用图6中的恢复方法进行处理。

图9 文献[6]中的切削振动信号

图10 不同二次采样频率下的双稳系统输出与恢复结果

由此可以看出，对于本实验中的周期性脉冲信号，类脉冲信号的恢复方法都可以得到较为理想的处理结果。由于单稳共振状态的参数调节范围远远大于双稳共振状态的调节范围，并且只需要改变二次采样频率的大小以获取重复性的时域信息，极大的降低了调节参数的数量和难度，因此与级联双稳随机共振相比，类脉冲信号的随机共振恢复方法具有更大的实用价值。

5 结论

本文把工程实际中普遍遇到的含噪信号分为“类正弦信号”和“类脉冲信号”，针对两类信号给出了不同的恢复方法，这两种方法的区别在于是否达到双稳共振状态，以及恢复系统参数是否固定。实验证明，基于信号分类的随机共振恢复方法，可实现工程中对含噪信号的特征提取。与二次采样和参数调节随机共振方法结合，亦可扩展到大频率范围内，对于噪声强度也具有一定的适应性。由于该法具有随机共振在信号处理中异于常规方法的优势，并且对信号周期性没有要求，因此有望在信号的时域处理中得到更加广泛的应用。对于类脉冲信号，建立二次采样频率srf和最佳恢复效果的关系，是下一步工作需要解决的问题。

[1] R.Benzi, A.Sutera, et al. The Mechanism of Stochastic Resonance[J], J. Phys.A,1981,14(11):L453-4572.

[2] L.Gammaitoni, P.Hänggi,et al. Stochastic Resonance[J],Rev. Mod. Phys.,1998,70(1): 223-285.

[3] 张莹, 王太勇,等. 双稳随机共振的信号恢复研究[J], 力学学报, 2008, 40(4): 528-534.

[4] Alfonsi L., Gammaitoni L.,Santucci S., et al, Intrawell stochastic resonance versus interwell stochastic resonance in underdamped bistable systems, Phys.Rev.E,2000,62(1):299-302.

[5] Gammaitoni L.,Hänggi P.,Jung P., et al,Stochastic Resonance, Rev. Mod. Phys., 1998, 70(1): 223-285.

[6] HE HL, WANG TY, et al. Study on non-linear filter characteristic and engineering application of cascadedbistable stochastic resonance system[J],Mechanical Systems and Signal Processing, 2007, 21(7):2740-2749.

[7] ZHANG Y, WANG TY, et al. Application of Stochastic Resonance Signal Recovery[J], Chinese Journal of Mechanical Engineering,2009, 22(4):542-549.

[8] 冷永刚,王太勇,级联双稳系统的随机共振特性Stochastic resonance behaviors of bistable systems connected in series.

[9] 冷永刚,王太勇,等.二次采样随机共振频谱研究与应用初探[J].物理学报,2004,53(3):717-723.

[10] Xu BH, Duan FB,Bao RH,et al.Stochastic resonance via tuning system parameters:The application of bistable system in signal processing[J].Chaos,Solitons&Fractals,2002,13(4):633-642.