建筑施工中极坐标放样精度分析

郭长宏

（胜利油田胜利勘察设计研究院有限公司，山东 东营257026）

0 前言

施工放样是按规定的精度和设计要求，将建筑物、构筑物的平面位置和高程位置放样到实地。放样的精确程度直接影响施工的精度，进而影响最终工程质量。随着建筑物趋于多样化，给施工测量提出了更高的要求，因此精度分析在施工测量方面显得尤为重要。近些年来，微电子学、光电技术和计算机科学技术的迅速发展，使得测量仪器不断更新换代，全站型电子速测仪的应用，改变了传统的放样方法，极大地降低了工程施工技术人员的劳动强度，提高了劳动效率，给测量放样工作带来一个较大的变革[1]。

影响放样点平面位置的误差主要包括控制点测量引起的误差和放样过程中所产生的误差,要保证放样的精度,可以分别考虑它们应满足的精度要求[2]。要使待放样点的平面位置的测设达到有关技术规程的要求,分析施工放样过程产生的误差对放样点位误差的影响,对施工测量工作具有很重要的实际意义。

1 建筑施工中放样方法

点的平面位置测设根据施工现场控制网的形式、现场条件、建筑物大小、测设精度和仪器工具及人员配备等不同，通常采用的方法有如下几种：极坐标法、角度交会法及GPS-RTK直接坐标法。

1.1 极坐标法放样

极坐标法放样不需要事先计算放样元素，只要提供坐标就行，操作方便简单。全站仪架设在设站点上，输入待定点的坐标，后视定向，反算方位角，仪器会自动计算测站与后视的方位角，将仪器向左右旋转到达设计的方向线上，接着通过测设距离，按照仪器提示棱镜前后移动，直至放样出设计的距离，完成点位的放样。

1.2 角度交会法放样

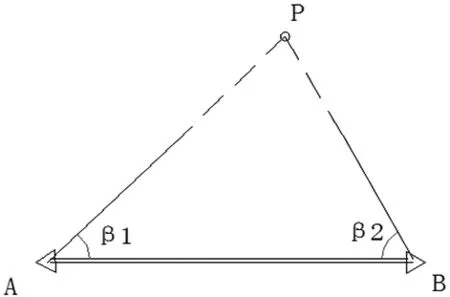
图1 角度交会法

角度交会法放样的原理及实现方法如图所示，根据两个已知点A、B的坐标和待定点P的设计坐标可以求得两个放样元素，即交会角β1、β2，现场放样时在两个已知点A、B上架设两架经纬仪，分别放样相应的角度β1、β2。两架经纬仪的视线的交点即是待定点P的平面位置。

1.3 GPS 直接坐标放样

GPS RTK需要一台基准站接收机和一台或多台流动站接收机以及用于数据传输的电台。RTK定位技术是将基准站的相位观测数据及坐标信息通过数据链方式及时传送给动态用户，用户将收到的数据链连同采集的相位观测数据进行实时差分处理，从而获得动态用户的三维位置。用户再将实时位置与设计值相比较，进而指导放样。

角度交会法适用于不便量距或控制点较远但能同时通视2-3个控制点时。GPS放样误差主要来源于GPS卫星星历、电离层散射、多路径效应、基准站坐标等。这样使得GPS-RTK放样精度较低，一般在1.5-3CM，难以在高精度建筑放样中应用。极坐标法放样能保证精度，同时操作简便，对一些形体复杂的建筑物放样工作有明显的优势，是目前较为常用的放样方法，为此本文重点对其放样精度进行分析。

2 极坐标放样精度分析

2.1 极坐标放样过程

极坐标法放样是利用数学中的极坐标原理，以两个控制点的连线作为极轴，以其中一点作为极坐标建立极坐标系，根据放样点与控制点的坐标，计算出放样点到极点的距离及该放样点与极点连线方向和极轴间的夹角。如下图所示，已知：A、B坐标及P点设计坐标，计算放样数据。

图2 极坐标放样

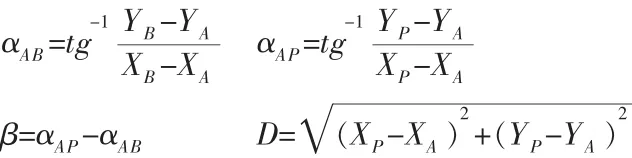
得出放样数据后，放样工作步骤如下：

1）在已知点A上安置仪器；

2）瞄准已知点B完成定向，并顺时针测设角度β，得到AP的方向；

3）沿着所测设的AP方向,测设距离D；

4）在地面上标定P点的位置并检核。

2.2 极坐标放样精度影响因素分析

由于各项工作都是互不相关发生,彼此均是独立的。按误差理论,用极坐标法测设P点时,放样过程中的各项误差对P点点位误差影响可按下式估算：

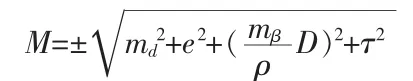
式中：md为水平距离测设的仪器误差；e为仪器的对中误差；mβ为角度的测设误差；τ为标定误差；D为距离；ρ为常数，值为206 265。

3 建筑施工中极坐标放样算例分析

建筑施工中常用的全站仪测角精度为±2″,测距精度为md=±(2+2×10－6D)，以此为例分析各项误差的来源及对放样点位误差的影响：

3.1 水平角测设误差的来源及影响

水平角测设的误差主要来源于下列几方面,即：望远镜照准误差、读数误差、仪器误差、目标偏心误差、测站偏心误差和外界条件的影响等。

3.1.1 望远镜照准误差ms。该误差与望远镜的放大倍数有关,取v=30，则 ms=±60″/v=±60″/30=2″

3.1.2 读数误差mr。 全站仪多次重复显示的读数差一般不超过1″,故读数误差为 mr=±1″。

3.1.3 仪器误差mi。仪器误差主要是竖轴的倾斜误差,因全站仪一般带有倾斜补偿装置,管水准器的分划值(30″/2 mm),故取 mi=±1.5″。

3.1.4 外界条件的影响mv。 据资料介绍,温度变 1°C,测角误差的变化范围在 0.27″-0.85″之间,故取 mv=±0.5″。

以上几项误差,它们都与所测距离无关,它们对半测回方向中误差影响为：

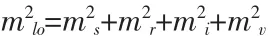
3.1.5 目标偏心引起的误差mp。在实际作业中,棱镜常采用带圆水准器的对中杆作为目标,由于圆水准器的精度为8′/2mm,假设对中杆的高度为 1.5m,目标偏心的偏离量为 8×60×1.5/206 265=3.5(mm),考虑其它因素的影响取4mm进行计算,若设测距长度为D,则由它引起的方向误差为：mp=±0.004×206 265″/D。

3.1.6 测站偏心引起的误差mo。测站偏心误差即测站点仪器对中时所产生的误差。采用光学对点器一般其误差不超过3mm,同样设边长为 D,则由此引起的方向测角误差为：mo= ±0.003 ×206 265″/D。 综合上述因素的影响, 半测回方向中误差为由此推算出半测回测角中误差为

3.2 水平距离的测设误差

放样过程中，测设距离的误差主要来源于仪器误差，测站偏心引起的距离误差等。

3.2.1 仪器误差 md。 仪器误差可取标称精度值，即 md=±(2+2×10-6D)mm。

3.2.2 测站偏心误差。由于测站光学对点器的对中误差一般不超过3mm，因此，测站偏心引起的距离误差可取±3mm，即e=±3mm，综合考虑上述因素，则测距中误差为

3.3 地面点的标定误差τ

引起地面点标定的因素主要有对中杆的偏心引起的误差和在地面上标记的误差。

3.3.1 对中杆偏心引起的误差m1。同前面目标偏心对角度影响的分析,推求得对中杆偏心可能引起的偏离量为4 mm,因而可取它对位置的标定误差的影响为m1=4mm。

3.3.2 地面上标记的误差m2。按通常的做法,精度要求较高的放样标记用小钉来进行,因而可取m2=3mm。

综合考虑两方面的因素,则标定误差为

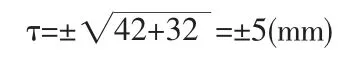
3.4 各项测设误差对放样点平面位置的综合影响值估算

根据上述对各项误差的分析和估计,取不同的D值,把各项误差代入,可求得各项误差对放样点位置中误差的影响如下表：

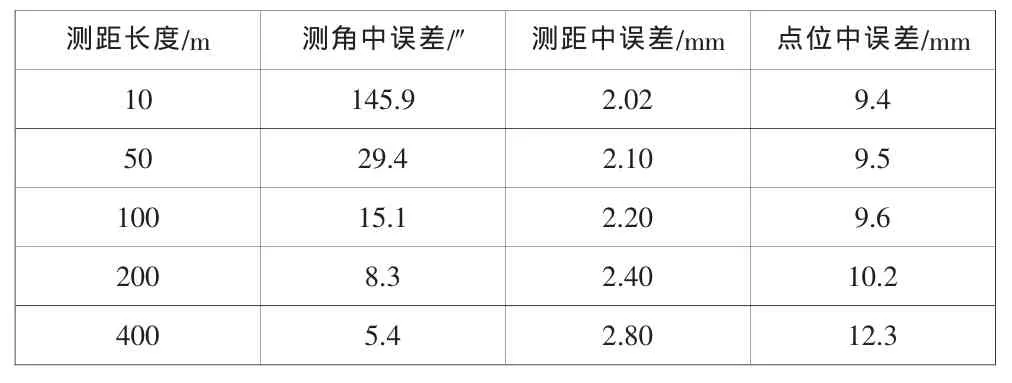
表1

从表中可看出,随着边长的增长,其角度测设的测角中误差减小较快,而距离测设的中误差和放样点点位误差的变化却不是很明显。考虑实地情况和工作效率,可选择比较适宜的放样边长，其中50-300m为比较适宜的放样边长。

4 结论与建议

现代工程的施工,通常采用同时交叉作业的方法,现场的施工机械、运输车辆、材料堆放等都阻挡视线。因此,现场放样的通视条件较差。采用极坐标法放样,它只需要在一个控制点上进行作业,仅需测设角度和量测控制点到放样点的距离，这样可以提高控制点的使用率,可以减少工作时间,提高工作效益。

［1］工程建设标准规范[S],GBJ50026-93 2测量规范[S].中国建筑工业出版社,1994-11.

［2］李青岳,陈永奇,等.工程测量学[M].湖北：测绘出版社,1997,02.

［3］贺占尧.全站仪放样道路中线的精度探讨[J].武汉大学测绘通报,2004,12.

［4］潘尚龙.全站仪、GPS 在建筑施工放样中的应用[J].建筑,2007,02.

［5］黄志奇.利用全站速测仪提高施工放样效率[J].山西建筑,2007,03.