基于任务的潜用导弹武器系统保障性仿真评价
2013-12-02王新华杨迎化
衡 辉,魏 勇,王新华,杨迎化
( 海军潜艇学院 导弹兵器系,山东 青岛266044)
0 引 言
导弹武器系统在使用阶段要经历多个任务过程,如技术准备阶段、航渡待机阶段、发射准备阶段、飞行阶段等。而其保障性的好坏与任务通知时刻或上一次任务结束时刻武器系统的状态及其保障系统的维修保障能力有关,对于那些在任务执行期间很难或根本不能进行维修保障的任务来说,任务准备阶段(从任务通知时刻到任务开始时刻)或任务间歇期(从上一次任务结束时刻到下一次任务开始时刻)的维修保障能力将直接影响到任务能否成功开始甚至成功完成。因此,在给定任务开始要求、任务通知时刻系统状态以及任务准备阶段的维修保障方案情况下,评价导弹武器系统任务准备阶段的保障性,对于实现复杂武器系统战备完好性评估与维修保障资源优化配置具有重要意义[1]。
目前,对保障性指标评价的仿真研究,国内学者则更多关注武器系统战备完好性和可用度研究[2-4],对基于任务的保障性评价研究很少,并且研究对象仅限于单一装备层次[5],对由多个同型装备及保障系统构成的装备基本作战单元并没有开展相关研究。尽管文献[6]提出了基于任务效能定义的任务持续性,但在工程上缺乏可操作性。本文旨在前人研究成果的基础上,考虑武器系统的任务需求和任务执行逻辑,首先给出基于任务的使用可用度、战备完好率及任务成功率3 个指标的定义;然后建立了使用可用度、战备完好率及任务成功率3 个评价指标的仿真统计模型;最后根据导弹的典型使用任务过程,通过Monte Carlo 法仿真模拟该过程,以此评价其保障性。
1 基于任务的保障性评价指标及仿真模型
1.1 保障性评价指标
表示装备保障性评价所采用的形式取决于系统、系统设计及使用条件。由于装备的类型、任务范围和使用特点各异,因而标识不同装备保障性评价的指标也不相同,不存在对所有装备系统都适用的统一的战备完好性度量参数。海军装备比较常用的保障性评价指标用使用可用度、战备完好率及任务成功率表示。各指标定义如下:
1)使用可用度(operational availability,AO):是指使装备服役后,在使用一段时间内使用时间与总时间的比值。使用可用度表达式为
AO=工作时间/ (工作时间+不能工作时间)。
在不考虑非工作时间的情况下,如果与任务时间相联系,总工作时间可以被定义为总的任务时间,能工作时间也就是系统完成任务的时间。因此,从任务角度考虑,AO又可以表示为
AO=系统完成任务的时间/总任务时间。
2)战备完好率(operational readiness probability,POR):是指当武器装备或武器系统(军事单位)投入作战时,该系统能够执行任务的概率。因此,从任务角度考虑,其可表示为:在规定的使用及维修保障方案下,系统能够执行的任务数与总任务数之比。其表达式为
POR=能够执行的任务数/总任务数。
3)任务成功率 (mission completion success probability,PMCS):是指在规定的任务剖面中完成任务成功性的概率,是装备任务成功完成总次数与任务执行总次数的比值。其表达式为
PMCS=任务成功完成的总次数/仿真的总次数。
1.2 仿真统计模型
评价指标仿真统计模型主要是完成所评价指标的统计输出,是保障性评价指标仿真统计的核心之一。各评价指标的仿真统计模型如下:
1)使用可用度统计模型
任一基本任务的完成都需要历经3 个阶段,如图1所示。
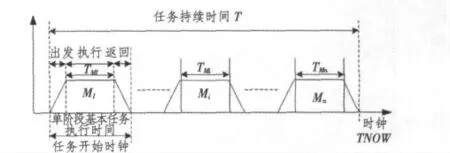
图1 多阶段固定任务时序模型图Fig.1 The time-sequenced model of multi-phase fixed task
执行任务时,只有当执行第i 个基本任务的时间大于第i 个基本任务要求的执行时间,即TFEi≥TMi时,任务才算完成。在任务执行过程中,如果执行到第i 个基本任务时,由于故障等原因,该任务没有成功完成,则第N_Sim 次仿真的任务累积时间将累加到第i-1 个基本任务完成时刻。设第i-1 个基本任务的任务序号为nMi-1,第N_Sim 次仿真时累积执行任务的时间为:
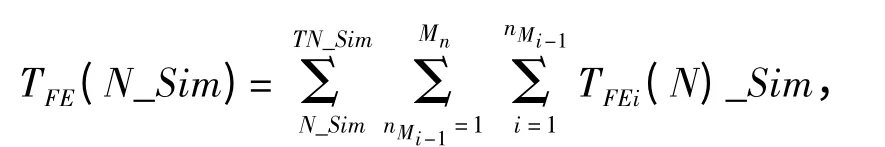
则使用可用度的仿真统计模型为
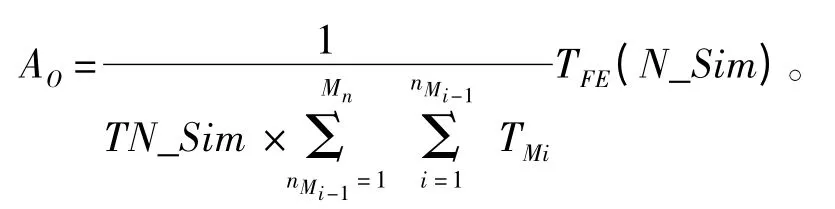
式中:Mi为第i 个基本任务,i=1,2,…,n;TMi为第i 个基本任务的执行时间;TFEi为实际执行第i个基本任务的时间;TN_ Sim 为总的仿真次数。
2)战备完好率统计模型[7-8]
假设在第N_Sim 次仿真时对第i 个基本任务开始执行的次数开始计数,记为NMSEi(N_Sim),则有
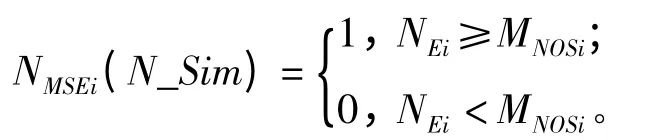
假设在第N_ Sim 次仿真时对第i 个基本任务成功执行的次数开始计数,记为NMSi(N_Sim),则有
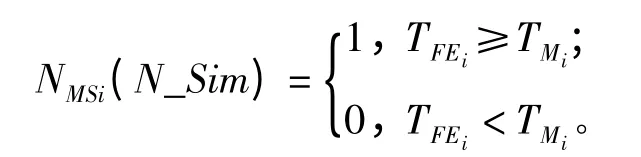
记在第N_ Sim 次仿真时第i 个基本任务能够执行的次数为NMEi(N_Sim),则有
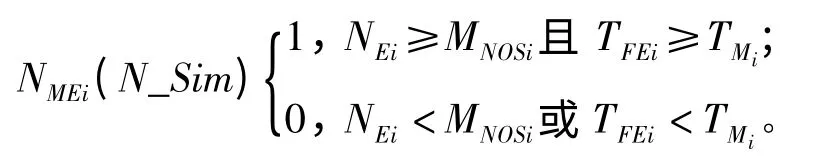
总的能够执行任务数
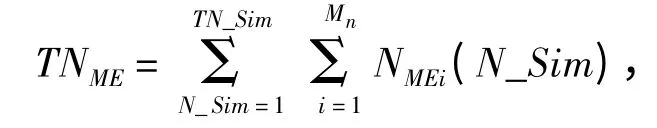
则战备完好率仿真统计模型为
POR=TNME/TN_SimxMn。
3)任务成功率统计模型
任务成功与否与装备故障引起的停机时间STD和任务允许的停机时间MRTD 有关。在第N_ Sim次仿真时,如果STD >MRTD,任务失败,记录任务失败次数NMF(N_Sim)=-1;反之,记录任务成功次数NMF(N_Sim)=1。因此,任务成功率仿真统计模型为
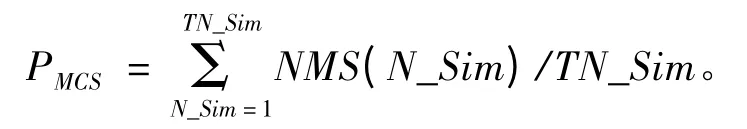
任务可靠性R 统计模型和置信度模型为[9]
R=成功试验任务数/总试验任务数(NMission)。
通过数理统计置信度模型得到的置信下限为
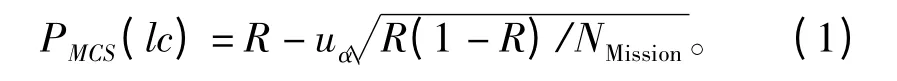
式中:α 为显著性水平,通常取α=0.9;1-α 为PMCS的置信水平;uα为α 的标准正态分布的分位数。
2 基于任务的保障性评价仿真原理
保障性仿真评价是依据装备任务剖面来对装备执行任务的方案进行仿真,主要着眼于装备的保障性、维修性以及保证装备在有限的维修保障资源情况下完成规定任务的能力。仿真中综合考虑任务需求和多级后勤保障组织,以任务为驱动,产生装备的各种事件(工作、故障、运输、修理等),根据装备在任务和维修工作中的状态,利用输出统计模型输出装备在任务阶段的战备完好性、任务成功性和保障能力等评价参数。保障性仿真评价原理如图2所示。
由评价指标模型知,其仿真利用Monte-Carlo仿真技术和事件调度法,在读取系统的设计参数和使用参数后,通过事件驱动依次模拟设备和系统在使用中的状态。仿真程序的具体流程如图3所示。
3 导弹武器系统保障性仿真
3.1 装备使用任务过程
图4 给出了典型的导弹装备使用任务过程,包含装备的技术准备、测试、待机、发射准备、故障维修等事件。本文所述仿真模型力图通过Monte Carlo 仿真原理来模拟图1 中所示装备的典型使用任务过程。
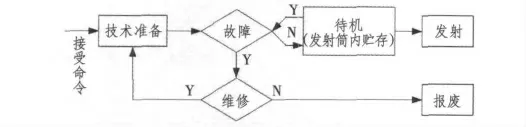
图4 简化的使用任务过程Fig.4 The process of simplified task using
3.2 设计与使用数据输入
案例中导弹的设计和使用数据主要包括在不同任务阶段的导弹各功能单元的平均故障间隔时间MTBF、单发导弹的MTTR、库存量、平均后勤保障延误时间MLDT 等。经优化,不考虑非任务件,导弹系统由5 个LRU 单元组成,该单元共包括107 个LRU 和121 个SRU,主要参数见表1。
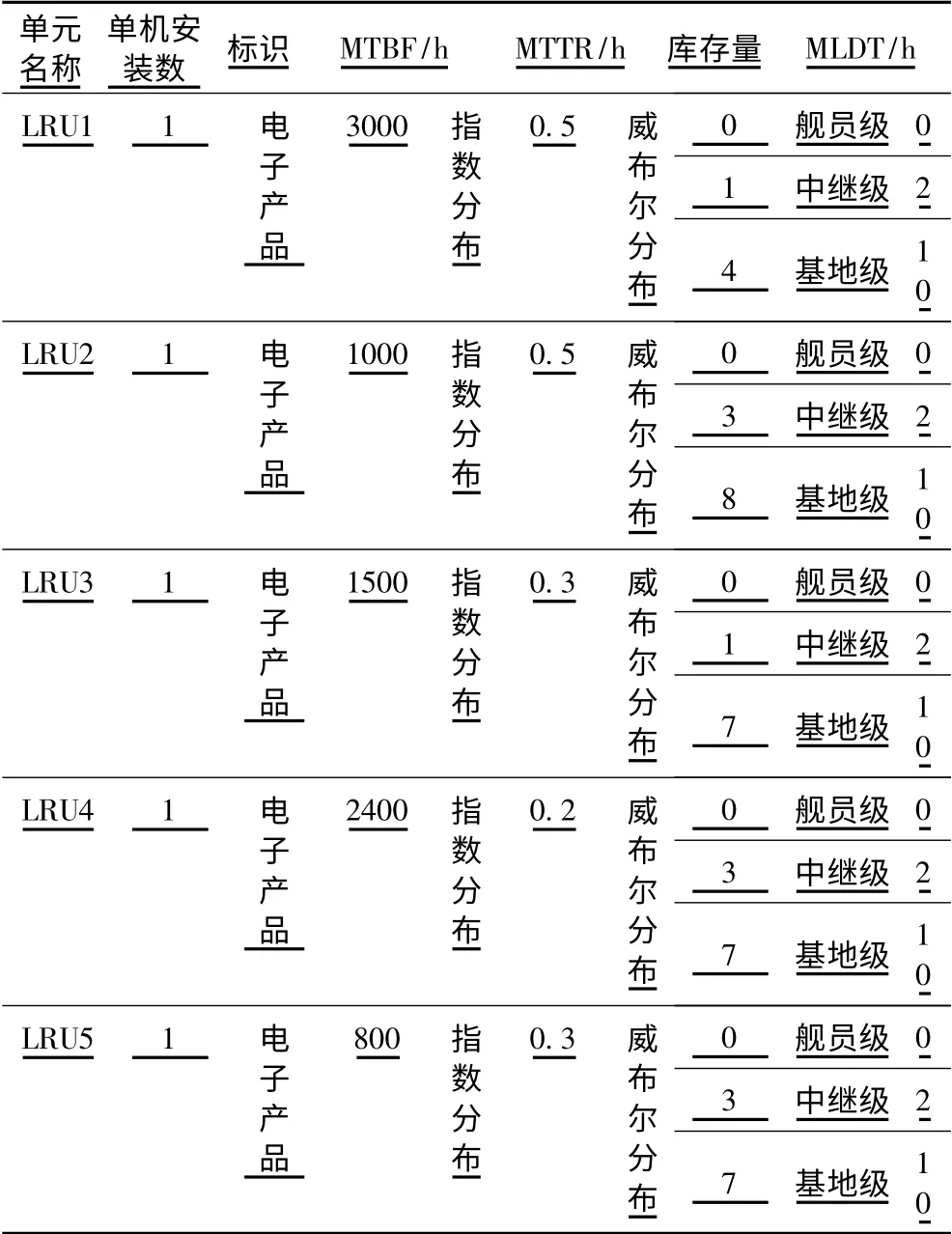
表1 功能参数表Tab.1 The table of function parameter
3.3 使用任务要求输入
导弹的使用任务要求参数包括任务要求的导弹数目、任务开始与结束时间、任务日历时间等参数。具体数据见表2所示。
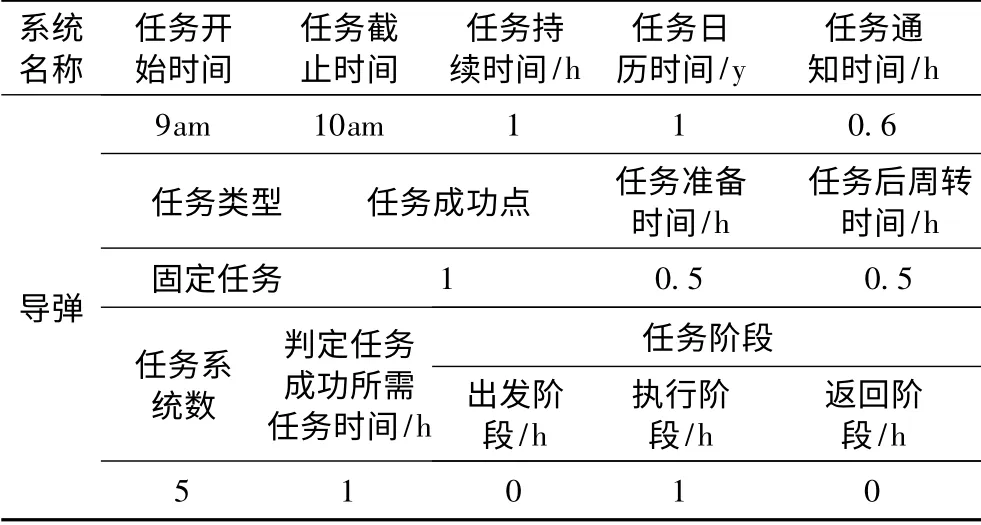
表2 使用任务参数表Tab.2 The parameter table of task using
3.4 仿真结果
针对上述数据,利用离散事件蒙特卡洛法对建立的仿真模型进行仿真,设定任务周期为1 200 h,即仿真周期为1 200 h,仿真次数为50 次,如表3所示。在一定的任务时间、维修保障方案及导弹的可靠性、维修性数据等的约束下,通过模型仿真计算,得出了导弹的使用可用度、战备完好率及任务成功率。
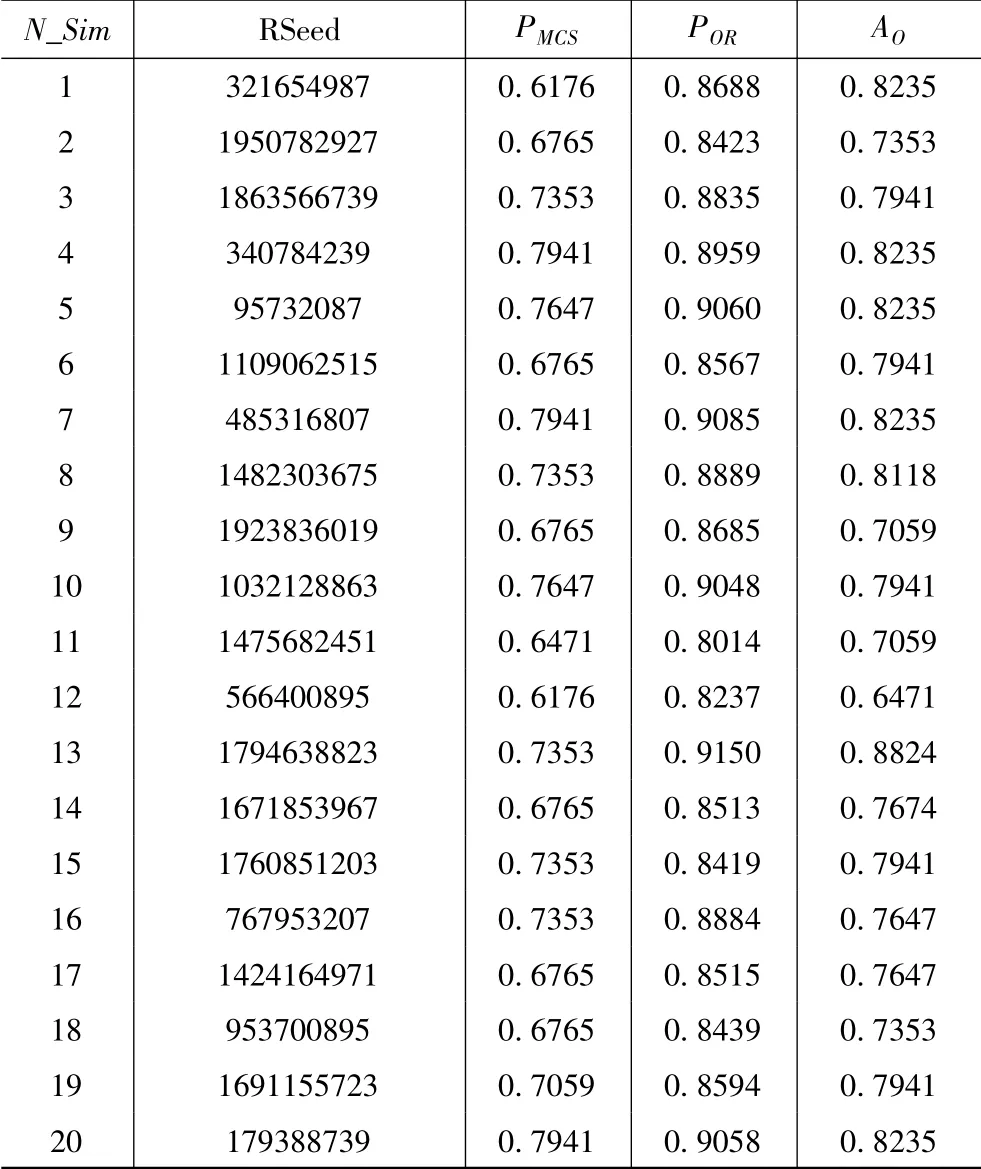
表3 仿真数据统计表Tab.3 The statistics table of simulation data
通过对仿真数据的统计,可以计算出任务可靠性(成功任务数/总任务数)为0.88。
取α=0.9,则由式(1)可得任务可靠性置信下限为0.821 2,任务成功率为0.711 8,使用可用度为0.780 4,战备完好率为0.870 3。
评价结果:已知任务规定要求为0.7,由于任务可靠性的置信下限大于规定的要求,装备满足保障性要求;从任务要求来看,与该任务所配置的保障系统是能够完成规定任务的。
4 结 语
本文通过对装备系统状态的分析,根据装备维修保障的运行机理,应用离散事件动态仿真原理,建立基于装备任务、保障组织及维修任务的仿真模型和仿真原理,并通过一个案例对模型和算法进行验证,得出了导弹武器装备系统的作战能力与保障能力的评价参数对装备使用部门和维修保障部门的管理决策具有一定的指导意义。
本文使用仿真的方法研究了装备使用与维修保障行为的特点,效果较好,但在模型设计上还存在局限性,主要表现在以下几点:
1)文中只对装备部件的寿命服从指数分布和维修时间服从威布尔分布的情况进行了研究。而在实际过程中,分布函数还有正态分布、伽马分布等,且获得这些分布函数需要进行大量的数据采集分析工作,如何获得这些分布函数还有待研究。
2)文中对备件需求的分布采用的是泊松分布,假定海军级备件库具有完全保障能力。而实际中,海军级备件库在备件短缺时需要订货,这也还有待研究。
3)文中只对装备LRU 层面的可更换单元进行了研究,实际中,每个可更换单元还可继续向下分解至最小单元,这样可以得到装备系统的详细结构层次。
[1]张建军,郭波,刘芳,张涛.任务准备阶段复杂武器系统战备完好率评估模型[J].系统工程与电子技术,2006.28(10):1534-1538.
ZHANG Jian-jun,GUO Bo,LIU Fang,ZHANG Tao.Model for evaluating the operational readiness of complex weapon system during the mission preparation period[J].Systems Engineering and Electronics,2006,28(10):1534-1538.
[2]焦健,王自力.军用飞机使用可用度仿真论证[J].北京航空航天大学学报,2006,32(1):112-116.
JIAO Jian,WANG Zi-li.Operational availability demonstration of military airplane based on simulation[J].Journal of Beijing University of Aeronautics and Astronautics,2006,32(1):112-116.
[3]虞兰,李泉生.应急备用装置的可用度与维修策略[J].机械设计与制造,1999(7):1-2.
YU Lan,LI Quan-sheng.Avaliability and maintenance of emergency standby equipment[J].Machiney Design and Manufacture,1999(7):1-2.
[4]李云峰.潜射弹道导弹武器系统可用度的计算模型[J].火力与指挥控制,2003,28(S):36-39.
LI Yun-feng.Research on model for operational availability of ballistic missile weapon system[J].Fire Control and Command Control,2003,28(S):36-39.
[5]ZHANG W J,KANG R,GUO L H,et al.Study on military equipment support modeling and simulation[J].Chinese Journal of Aeronautics,2005,18(2):142-146.
[6]聂成龙,张柳,于永利.多阶段任务系统任务持续能力仿真模型研究系[J].系统仿真学报,2008,20(3):729-737.
NIE Cheng-long,ZHANG Liu,YU Yong-li.Research to PMS mission sustainability simulating models[J].Journal of System Simulation,2008,20(3):729-737.
[7]郭霖瀚,康锐.基本作战单元任务持续性仿真度量模型研究[J].系统仿真学报,2009,21(2):325-329.
GUO Lin-han,KANG Rui.Individual operational unit sustainability simulation measure model research[J].Journal of System Simulation,2009,21(2):325-329.
[8]MIRACLE W B.Just-in-time effects on peacetime efficiency and wartime readiness[D].Master′s Thesis,ADA383919,Army Command and General Staff Coll.,Fort Leavenworth,KS.,1999.
[9]程文鑫,陈立强,龚沈光,等.基于蒙特卡洛法的舰船装备战备完好性仿真[J].兵工学报,2006,27(6):1090-1094.
CHENG Wen-xin,CHEN Li-qiang,GONG Shen-guang,et al.Readiness simulation of ship equipment based on Monte-Carlo method[J].Acta Armamentarll,2006,27(6):1090-1094.
