框架-核心筒超限高层结构的抗震性能评估*

杨春 潘健明 蔡健† 廖祥盛 李光星

(1.华南理工大学土木与交通学院，广东广州 510640;2.华南理工大学亚热带建筑科学国家重点实验室，广东 广州 510640;3.广州城建开发设计院有限公司，广东 广州 510620)

随着社会经济的发展，框架-核心筒结构越来越多地出现在超高层建筑结构中.鉴于该类结构的迅速发展，人们越来越关注其抗震性能.对于超限的框架-核心筒结构，更需要对其进行抗震性能研究和评估［1-5］.GB 50011—2010《建筑抗震设计规范》和JGJ3—2010《高层建筑混凝土结构技术规程》中新增了结构抗震性能设计内容，明确地给出了抗震性能目标与抗震性能水准，特别提到对超限结构进行抗震性能设计的重要性.对超限结构进行抗震性能设计，就是通过对结构进行试验或者数值模拟分析，确定结构的不规则程度，找出结构可能出现的薄弱部位，并对结构薄弱部位进行加强，以达到预期的抗震性能目标［6-9］.

在此背景下，文中针对某框架-核心筒超高层结构进行基于性能的抗震性能评估，利用三维结构非线性分析与抗震性能评估软件Perform 3D［10］对该框架-核心筒结构进行罕遇地震下的动力弹塑性时程分析，提出以结构整体地震响应、材料应变、主要受力构件变形作为抗震性能评估指标，从结构整体和局部的地震响应层面上，综合考察结构设计是否满足预期的抗震性能目标.

1 工程概况

该框架-核心筒结构建筑高309 m，两层地下室，地面以上主体结构68 层(另加机房层，共69 层)，结构首层层高6m，第二至四层层高5m，其他标准层层高均为4.5 m，建筑平面尺寸为48.1 m ×58.0 m，高宽比约为6，外围框架柱均为钢管混凝土柱，63 层以上平面内缩，内缩前后结构刚度比达到1.88.结构在第18 层、35 层和52 层的外围框架柱之间以及柱与核心筒之间布置了3 种不同截面的钢支撑，以增强结构整体抗侧刚度.结构平面布置如图1 所示.钢管混凝土柱和筒体剪力墙构件的截面和材料强度等级如图2 所示.建筑结构安全等级为二级，结构重要性系数γ=1.0;抗震设防烈度为6 度，设计地震分组为第一组，抗震设防分类为乙类［11］.

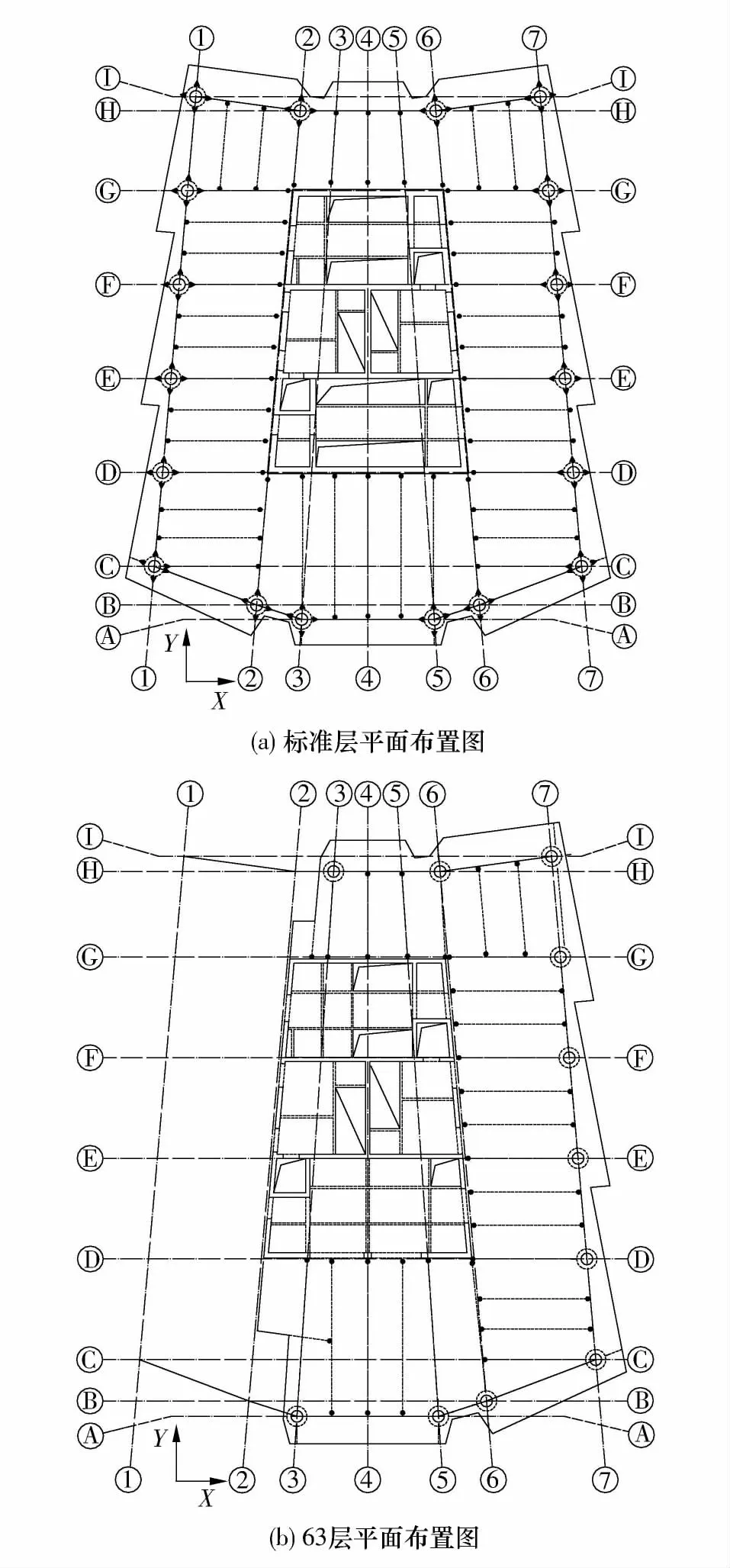
图1 结构平面布置图Fig.1 Plan layout of the structure

图2 主要构件截面尺寸和材料强度Fig.2 Dimensions and material strength of main components

结构超限情况如下:(1)结构高309 m，超出B 级高度89 m，高度超过规范限值;(2)楼板局部不连续;(3)平面扭转位移比为1.4，属于平面扭转不规则结构;(4)有局部夹层和转换，楼层承载力有突变.

该结构各主要构件的抗震性能目标如表1 所示.

表1 结构各构件抗震性能目标Table 1 Seismic performance objectives of structure components

2 结构分析

由于结构存在高度超限和体型超限问题，采用Perform 3D 非线性软件进行动力弹塑性时程分析.有限元分析模型中，材料强度均采用标准值;钢材与钢筋采用不考虑屈曲的两折线本构模型;混凝土采用Mander 约束混凝土本构模型［12］;钢管混凝土柱中核心混凝土本构模型则根据“钢管混凝土统一理论”的约束混凝土应力-应变关系来确定［13］，考虑强度退化，采用Perform 3D 提供的三折线本构模型来模拟;梁柱单元采用纤维模型;剪力墙采用宏观分层单元模拟.模型分析中，采用瑞利阻尼进行计算，阻尼比取4%.

为保证模型的可靠性，表2 对比了Satwe、Etabs和Perform 3D 3 个软件计算得到的前6 阶周期.通过对比可见，不同软件的计算结果吻合较好，结构分析模型可靠.图3 所示为采用Perform 3D 计算得到的前3 阶振型图.其中，第1、第2 阶振型分别为X 向和Y 向平动，第3 阶振型为平面扭转.通过Satwe 的计算结果可知，结构扭转为主的第1 阶自振周期与平动为主的第1 阶自振周期之比为0.337，满足规范要求.

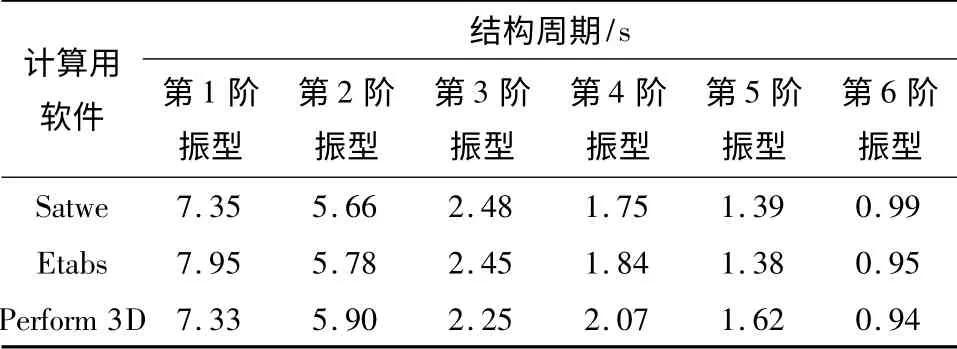
表2 不同软件计算得到的结构周期Table 2 Structural periods calculated by different softwares

图3 Perform 3D 计算得到的结构前3 阶振型图Fig.3 First three vibration diagrams of the structure calculated by Perform 3D

3 动力时程分析

为了合理地评估结构地震反应，经过对多条天然波进行频谱分析，并且根据《建筑工程抗震性态设计通则》、结构自振周期和场地土类别，选取震级较大、震中距较小的6 条天然波(取自太平洋地震工程研究中心地震动数据库)和1 条安评报告提供的地震波(人工波)进行动力时程分析，各地震波的持时为35～40 s，峰值加速度为145 gal.6 条天然波的具体参数如表3 所示.

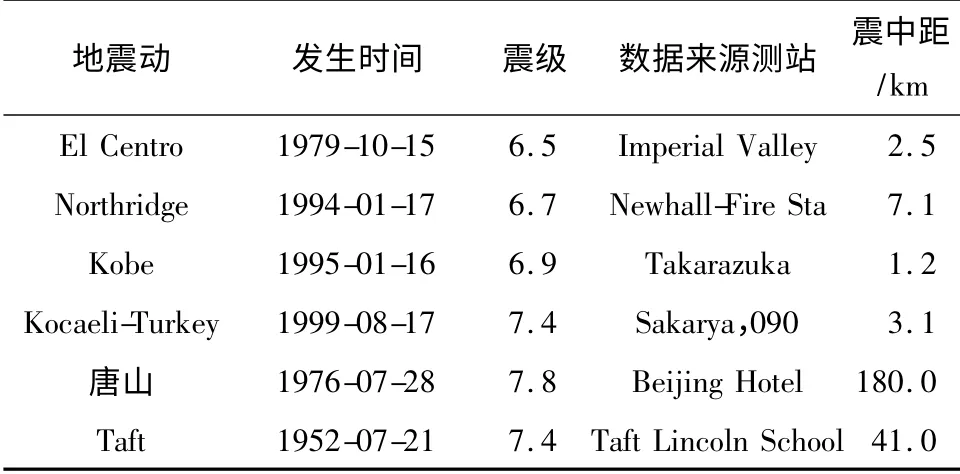
表3 天然波的参数Table 3 Parameters of natural seismic waves

3.1 结构顶点位移曲线

由结构的平面布置图可知，结构的X 向为结构的弱轴方向，因此文中主要分析地震动沿X 方向作用时结构的地震反应.

限于篇幅，考虑到结构在人工波和El Centro 波作用下地震响应最大，在此仅给出框架-核心筒结构在人工波和El Centro 波作用下的顶点位移时程曲线，如图4 所示.结构在各个地震动作用下的最大顶点位移如表4 所示.由表4 可见，不同地震波作用下结构的最大顶点位移相差较大，在Kocaeli-Turkey 波作用下反应最为剧烈，在唐山波的作用下反应最小.

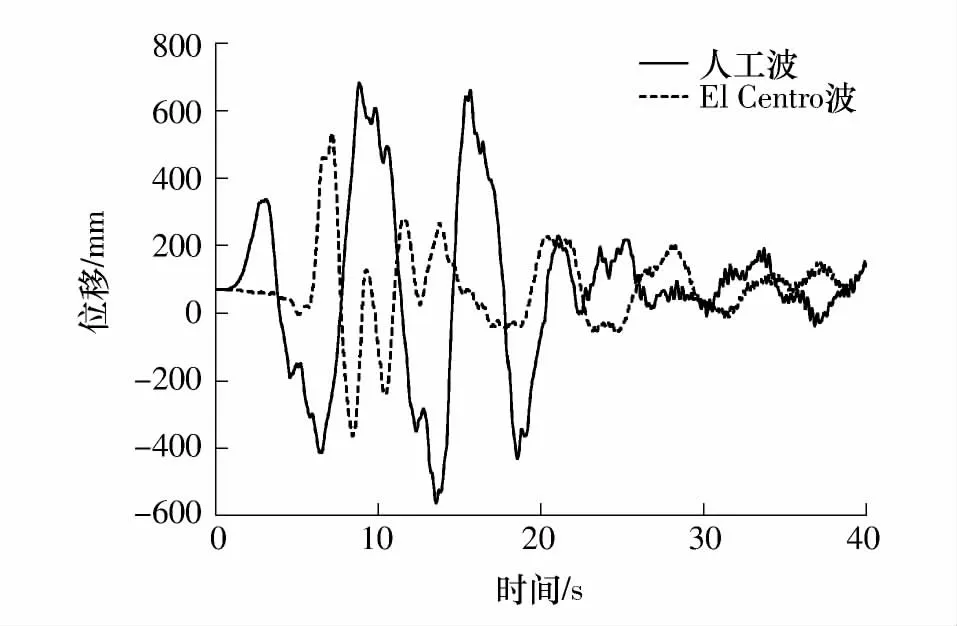
图4 人工波和El Centro 波作用下结构的顶点位移时程曲线Fig.4 Time-history curves of top displacement under artificial seismic wave and El Centro wave

表4 各个地震动作用下结构的最大顶点位移Table 4 Maximum top displacements of structure under different seismic waves

3.2 结构最大层间位移角曲线

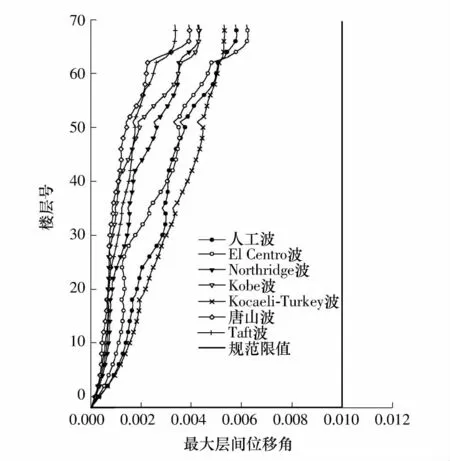
图5 各个地震动下各楼层的最大层间位移角Fig.5 Maximum inter-story drift angle of each story under different seismic waves

结构在各个地震动作用下各楼层的最大层间位移角曲线如图5 所示.由图5 可知，由于结构平面在第63 层缩进面积较大，抗侧刚度在此出现较大突变，各楼层层间位移角曲线在第63 层处附近发生突变.结构各楼层的最大层间位移角出现在第67 层，其中，人工波和El Centro波作用下最大层间位移角分别为1/172 和1/160，均小于规范限值(1/100)，满足规范要求.

3.3 结构基底剪力时程曲线

人工波和El Centro 波作用下结构的基底剪力时程曲线如图6 所示，各个地震动作用下结构的最大基底剪力如表5 所示.由表5 可见，各个地震动作用下结构的最大基底剪力差别较小，最大值与最小值相差不足1.5 倍，保证了结构的计算结果不会出现较大的离散.

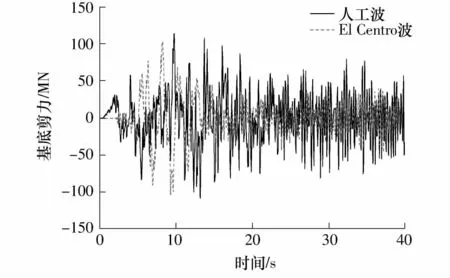
图6 人工波和El Centro 波作用下结构的基底剪力时程曲线Fig.6 Time-history curves of base shear force under artificial seismic wave and El Centro wave

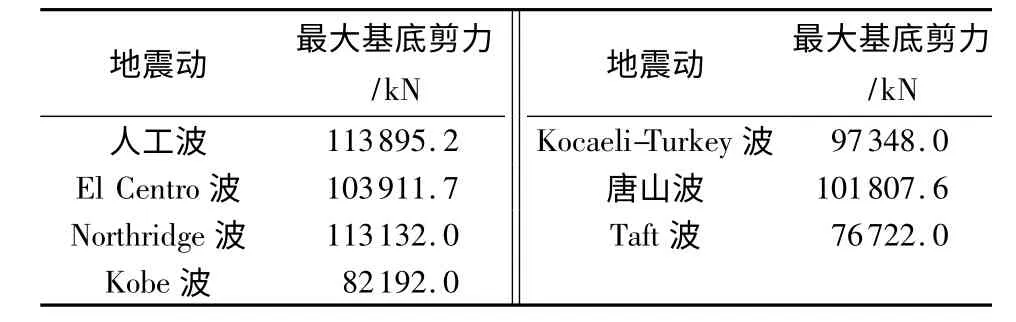
表5 各个地震动作用下结构的最大基底剪力Table 5 Maximumbase shear force of structure under different seismic waves

4 结构损伤状况分析

为探究在罕遇地震动作用下结构主要受力构件处于何种损伤破坏状态，分别以混凝土的极限压应变εcu来划分混凝土受压时的各个破坏状态，以钢筋的极限拉应变εst来划分钢筋受拉时的各个破坏状态.定义混凝土受压应变需求比γ1和钢筋受拉应变需求比γ2为

其中:εperc和εpers分别表示由Perform 3D 计算获得的构件混凝土最大压应变和钢筋最大拉应变;εcu表示混凝土强度下降50%时对应的极限压应变［14］;εst表示钢筋极限拉应变，取值为0.025.构件在不同损伤状态下的最大应变如表6 所示.

在人工波(损伤破坏较大工况)作用下，结构的损伤分布状况如图7所示.图中灰色表示需求比不超过0.4，蓝色表示需求比介于0.4～0.6 之间，绿色表示需求比介于0.6～0.8 之间，橘色表示需求比介于0.8～1.0 之间.

表6 构件在不同损伤状态下的最大应变Table 6 Maximum strain of components under different damage status

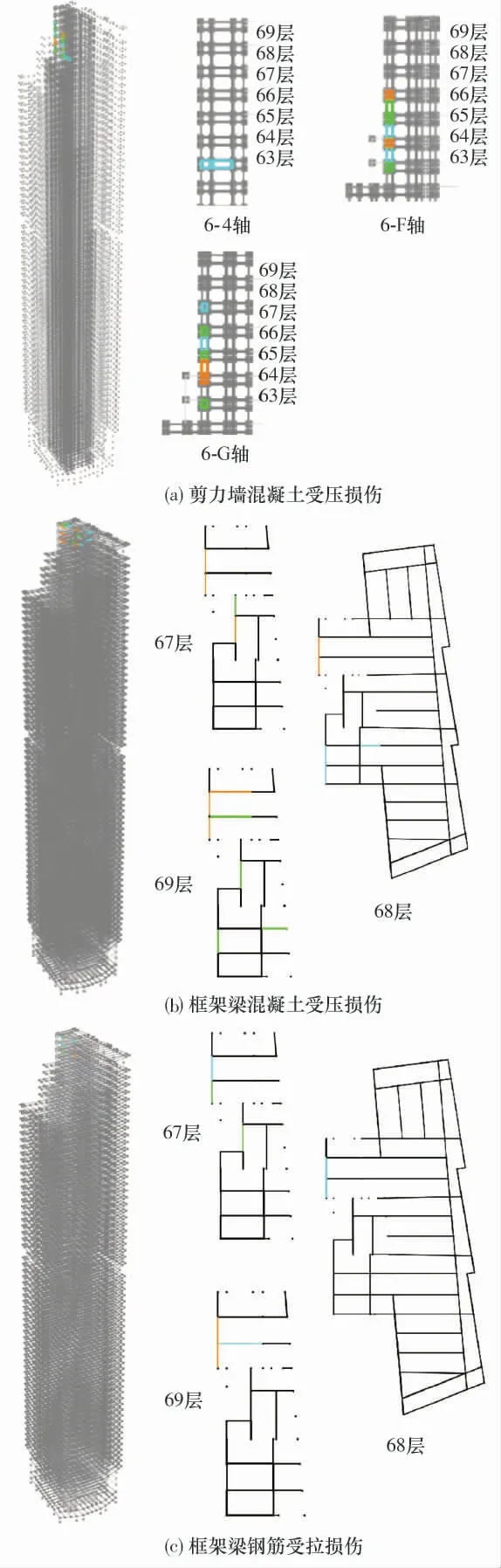
图7 人工波作用下结构的损伤分布Fig.7 Distribution of structural damage under artificial seismic wave

根据人工波的计算结果，连梁和钢管混凝土柱均没有出现损伤，基本处于完好状态，结构的损伤主要出现在顶部的梁和剪力墙构件上，如图7 所示.结构平面缩进处附近的楼层剪力墙损伤较大，6-F 轴64、66 层以及6-G 轴65 层局部剪力墙出现中度损伤，其中最大需求比出现在结构的6-G 轴65 层，为0.81.但是，根据JGJ3—2010《高层建筑混凝土结构技术规程》第4.3.5 条第4 款规定，当取7 组及7 组以上时程曲线进行计算时，结构地震作用效应可取平均值.依此规定，6-F 轴66 层剪力墙平均需求比为0.32，6-G 轴65 层剪力墙平均需求比为0.37，需求比均小于0.4，处于基本完好阶段.因此，建议对人工波作用下出现中度损伤的剪力墙进行局部加固，但是根据规范要求取平均值后整体结构基本保持完好，仍能达到预定的性能目标要求.

各楼层钢支撑最大轴压应力与最大轴拉应力如表7 所示.由表7 可知，各支撑的最大应力均小于钢材的屈服应力345 N/mm2，所有钢支撑均处于弹性状态.

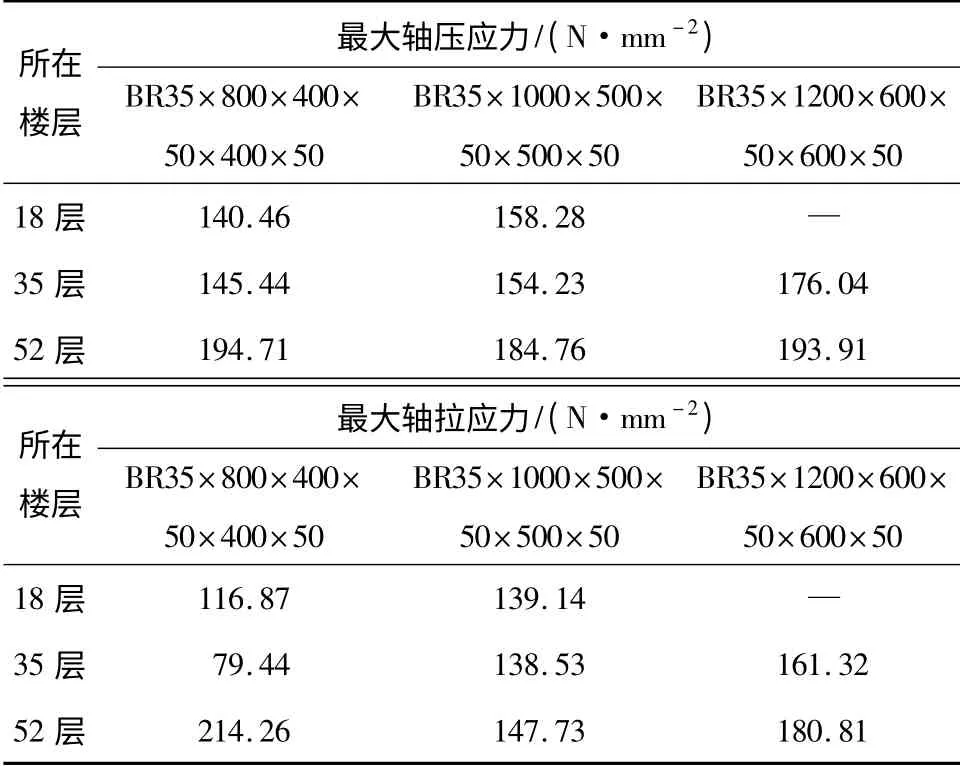
表7 钢支撑最大轴压应力与轴拉应力1)Table 7 Maximum compressive and tensile stresses of steel supports

5 剪力墙构件变形性能分析

为进一步评估结构中剪力墙的抗震性态，对结构剪力墙构件在罕遇地震作用下的变形性能进行分析.参考美国规范ASCE 41［15］中关于构件变形性能指标限值的规定，并结合该结构剪力墙的配筋构造及内力情况，确定剪力墙构件转角的三阶段性能水平为:基本完好(IO)、生命安全(LS)、接近倒塌(CP).各性能水平对应的剪力墙转角限值为:IO 阶段转角不超过0.003rad，LS 阶段转角不超过0.006rad，CP 阶段转角不超过0.009 rad.

人工波作用下结构剪力墙的塑性转角分布状况如图8 所示.由图8 可见:大部分整体剪力墙构件处于IO 状态;第63 层以上6-F 轴和6-G 轴部分墙肢处于LS 状态，其中最大塑性转角为0.005 4 rad，出现在65 层6-G 轴的边缘墙肢上.由结构整体剪力墙塑性转角状况可知，结构处于弱非线性状态.

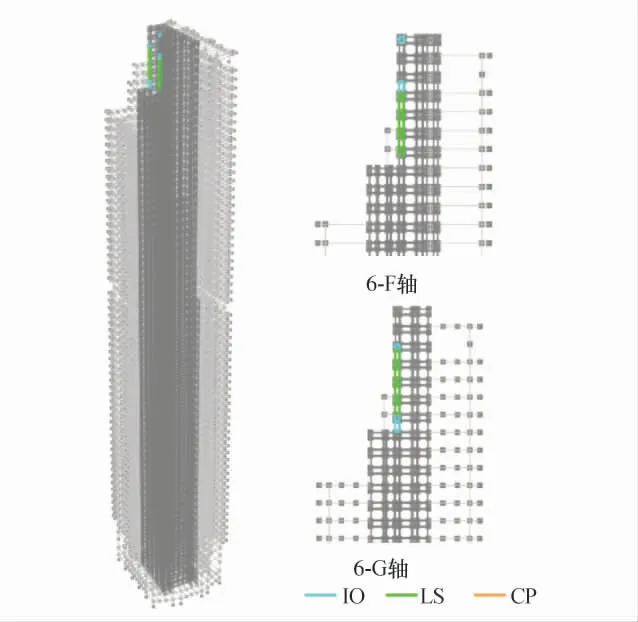
图8 整体剪力墙结构的塑性转角性能Fig.8 Plastic rotation capacity of the whole shear wall structure

6 结论

文中从结构整体和构件层面上对框架-核心筒超限高层结构进行抗震性能评估，主要得到以下几点结论:

(1)通过分析结构整体地震响应可知，在不同的地震动作用下，结构最大层间位移角为1/160，小于规范限值(1/100)，结构整体变形满足规范要求.

(2)根据结构构件的内力和变形分析可知，大部分剪力墙、连梁、框架柱及钢支撑均处于基本完好状态，仅位于结构平面缩进处的剪力墙和框架梁在人工波作用下出现中度损伤破坏，但取其平均值后变形值仍处于基本完好状态;进一步分析剪力墙的变形性能可知，大部分剪力墙的变形均处于弹性范围，结构平面缩进处部分墙肢则发生较大弹塑性变形，但仍处在生命安全状态.

(3)从结构整体和局部的地震响应层面上，综合结构整体地震响应、材料应变、主要受力构件变形的评估分析可知，该框架- 核心筒超限高层整体结构处于弱非线性状态，可达到预期的抗震性能目标.

［1］白国良，楚留声，李晓文.高层框架-核心筒结构抗震防线问题研究［J］.西安建筑科技大学学报:自然科学版，2007，39(4):445-450.Bai Guo-liang，Chu Liu-sheng，Li Xiao-wen.The research on the problem of earthquake fortification line in high-rise frame-core wall structures［J］.Journal of Xi'an University of Architecture ＆ Technology:Natural Science Edition，2007，39(4):445-450.

［2］徐培福，傅学怡，王翠坤，等.复杂高层建筑结构设计［M］.北京:中国建筑工业出版社，2005.

［3］Shahrooz B M，Gong B N，Tunc G，et al.An overview of reinforced concrete core wall-steel frame hybrid structures［J］.Progress in Structure Engineering and Materials，ASCE，2001，3(2):149-158.

［4］徐培福，薛彦涛，肖从真，等.高层型钢混凝土框筒混合结构抗震性能试验研究［J］.建筑结构，2005，35(5):3-8.Xu Pei-fu，Xue Yan-tao，Xiao Cong-zhen，et al.Experimental study on seismic performance of high-rise SRC hybrid structures［J］.Building Structure，2005，35(5):3-8.

［5］韩小雷，唐剑秋，黄艺燕，等.钢管混凝土巨型斜交网格筒体结构非线性分析［J］.地震工程与工程振动，2009，29(4):77-84.Han Xiao-lei，Tang Jian-qiu，Huang Yi-yan，et al.Nonlinear analysis of huge oblique crossing lattice structure with concrete filled steel tube［J］.Journal of Earthquake Engineering and Engineering Vibration，2009，29(4):77-84.

［6］徐培福.关于超限高层建筑抗震设防审查的若干讨论［J］.土木工程学报，2004，37(1):1-12.Xu Pei-fu.Discussion on review of seismic fortification tall buildings with design beyond the code limits［J］.China Civil Engineering Journal，2004，37(1):1-12.

［7］徐培福，戴国莹.超限高层建筑结构基于性能抗震设计的研究［J］.土木工程学报，2005，38(1):1-10.Xu Pei-fu，Dai Guo-ying.Performance-based seismic design of tall building structure beyond the code-specification［J］.China Civil Engineering Journal，2005，38(1):1-10.

［8］Fragiadakis M，Papadrakakis M.Performance-based optimum seismic design of reinforced concrete structure［J］.Earthquake Engineering and Structure Dynamics，2008，37(6):825-844.

［9］吴晓涵，刘东泽，芮明倬，等.非对称刚性连体超高层结构弹塑性时程分析［J］.建筑结构学报，2011，32(6):1-9.Wu Xiao-han，Liu Dong-ze，Rui Ming-zhuo，et al.Elastoplastic time history analysis of asymmetrical rigid-connected twin-tower structure［J］.Journal of Building Structures，2011，32(6):1-9.

［10］韩小雷，陈学伟，林生逸，等.基于纤维模型的超高层钢筋混凝土结构弹塑性时程分析［J］.建筑结构，2010，40(2):13-16.Han Xiao-lei，Chen Xue-wei，Lin Sheng-yi，et al.Elastoplastic time-history analysis of super high-rise RC structure based on fiber model［J］.Building Structure，2010，40(2):13-16.

［11］杨春，何铭基，潘健明.武汉硚口区金三角项目6#写字楼罕遇地震弹塑性时程分析报告［R］.广州:华南理工大学，2012.

［12］Mander J B，Priestley M J N，Park R.Theoretical stressstrain model for confined concrete［J］.Journal of Structural Engineering，1988，114(8):1804-1826.

［13］钟善桐.钢管混凝土统一理论——研究与应用［M］.北京:中国建筑工业出版社，2005.

［14］GB50010—2010，混凝土结构设计规范［S］.

［15］ASCE 41，Seismic Rehabilitation of existing buildings［S］.