有效逼近MIMO信道容量的软解调算法*

蔡曙 黑永强

(西安电子科技大学 综合业务网理论及关键技术国家重点实验室，陕西 西安 710071)

多输入多输出(MIMO)系统在不增加系统带宽的前提下，能够极大地提高无线通信的数据传输速率，因而被视为下一代无线通信极具潜力的核心技术之一.发送端采用比特交织编码调制、接收端采用基于比特软信息迭代的解调器和译码器［1-8］的Turbo-MIMO 系统［2，4］，因能够逼近MIMO 信道的香农容量限而引起了国内外学者的广泛关注.然而，困扰Turbo-MIMO 系统的一大难题是缺乏高效的软解调算法.由于最优软解调最大后验概率(MAP)准则的复杂度随着问题维数呈指数增长［1］，因此，低复杂度高性能的软解调算法成为研究的一大热点.

为降低软解调算法的复杂度，学者们提出了一系列复杂度较低的近似最优的解调算法［1-3，9-10］.其中，对MAP 准则进行Max-Log-MAP 近似是降低复杂度的关键.在此基础上，文献［10］中提出了基于半正定松弛的低复杂度正交相移键控(QPSK)信号的软解调算法，但其误码率较高.为降低计算复杂度，文献［1］中提出了一种列表球形译码(LSD)算法，文献［3］中将软解调问题转变成一系列球形译码(SoD-HSD)问题再求解.这类基于球形译码的软解调算法的解调复杂度有所降低，约为Nt(Nt为发射天线数)次球形译码的复杂度.然而，当信噪比较低或问题的维数较高时，球形译码本身可能呈现指数级的复杂度［11-12］，并且对于不同的信道实现，其运行时间差别会很大.PSK 信号系统采用QML-PSK检测算法［11，13］进行软解调［9］，是进一步降低解调复杂度的一种有效求解思路，但QML-PSK 检测算法不适用于高阶QAM 星座图.因此，针对高阶QAM 星座图实现高性能低复杂度软解调仍是一个值得深入探讨的问题.

针对球形译码复杂度高的问题，文中将QMLPSK 检测算法应用于Turbo-MIMO 系统中，提出了一种低复杂度的QAM-PSK 软解调算法.该算法采用比特级多流编码分层空时(LST)传输技术，将高阶QAM 信号转换成PSK 信号，以实现对任意QAM星座图的低复杂度QML-PSK 软解调.在此基础上，根据比特流分层传输时各层比特的信噪比不同，通过消除低信噪比比特解调错误对高信噪比比特解调的影响来改进QAM-PSK 软解调算法.文中最后对所提QAM-PSK 软解调算法进行了复杂度分析，并通过仿真验证其在性能和复杂度上的优势.

1 系统模型

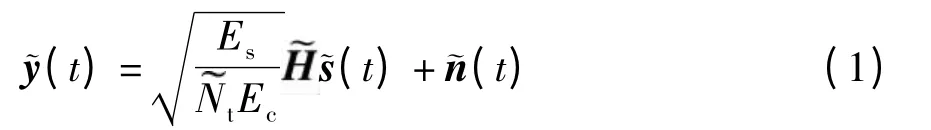
式中:Ec是信号(t)的平均能量;Es是总发射功率;是复信道矩阵(t)是服从CN(0，σ2I)分布的复加性高斯白噪声(AWGN)，信号和噪声均随时间序列t 变化，σ2为噪声方差;(t)中的每个元素由Mc个经过差错控制编码和交织后的比特在2McQAM 星座图上映射产生.不失一般性，为方便起见，对式(1)中的参数实数化，即

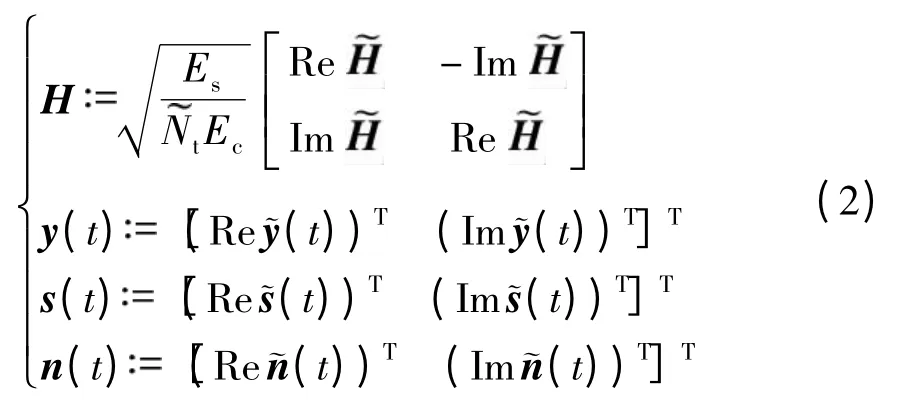
式中，向量s(t)的维数为Nt，其元素由M(M=Mc/2)个经交织后的编码比特在2MPAM 星座图C 上映射得到，C 对应于2McQAM 星座图的实部或虚部.

在接收端，Turbo-MIMO 接收机的软解调器首先根据信号y(t)和待解调向量s(t)中MNt个二进制编码比特{xk(t)}的先验信息{LA(xk(t))计算其外信息LE(t)=(LE(x1(t )y(t))，LE(x2(t)y(t))，…，LE(xMNt(t)y(t)))T，并将所有比特的外信息送入软输入软输出译码器，从而更新编码比特的先验信息或最终判决输出.

可见，Turbo-MIMO 接收机的复杂度取决于信号软解调和译码两部分.目前，译码算法(如BCJR 译码［14］)相对比较成熟，复杂度改进空间不大，因此如何改进软解调器成为降低接收机计算复杂度的关键，而这正是文中所提出的低复杂度QAM-PSK 软解调算法的出发点.

为方便描述，以下推导中省略时间序号t，则式(3)可简化成

当编码比特之间相互独立时，由贝叶斯准则可知，软解调算法所要求解的比特外信息可以表示为［1］

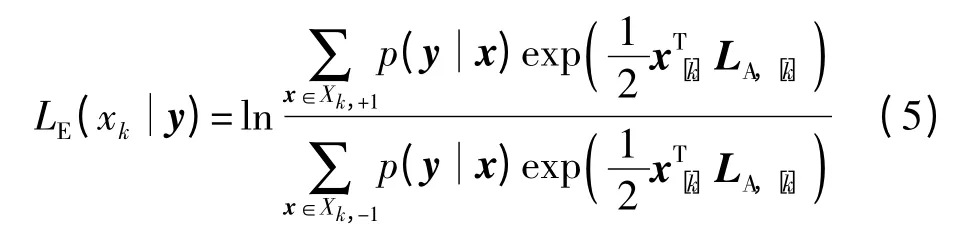
式中，x 是s 中的MNt编码比特所组成的向量，Xk，+1和Xk，-1分别是xk=1 和-1 时x 的取值集合，x［k］是向量x 剔除xk后的向量，xk的先验信息为LA(xk)=ln(p(xk= +1)/p(xk=-1))，似然函数p(yx)∝exp(-y- Hs2/(2σ2)).定义LA= (LA(x1)，LA(x2)，…，LA(xMNt))T，则式(5)中的LA，［k］表示LA剔除LA(xk)后的向量.

通过式(5)直接求解LE(xky)的复杂度为O(2MNt)［1］，此时不妨对式(5)进行Max-Log 近似，这样能够以很小的性能损失获得复杂度的大幅降低［1-3，9-10］.将近似后的公式进一步化简，可得

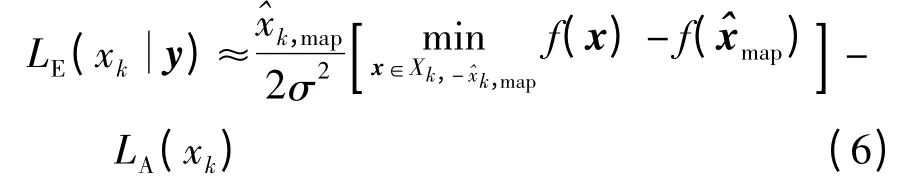
式中，f(x)= y-Hs(x)2-σ2xTLA，s(x)是由比特向量x 在星座图上映射得到的s 向量，^xmap是的最优解，k，map是map的第k 个元素.由式(6)易知，高效求解外信息LE(xky)的关键在于高效求解优化问题和

2 QAM 星座图的高效软解调算法

为有效求解式(6)，文中引入QML-PSK 检测算法，并利用比特级多流编码LST 传输技术，提出一种能适用于各种QAM 星座图的QAM-PSK 软解调算法.

2.1 QML-PSK 检测算法及其在PSK 星座图中的软解调算法

在MIMO 无线通信系统中，当发射信号为QPSK 时，可根据式(2)将QPSK 实数化为BPSK 信号s，有s=x.在AWGN 环境下，最大似然(ML)检测可表示为［10］

其复杂度随问题的维数呈指数增长.为降低复杂度，可将整数约束松弛为复数恒模约束，即x∈Nt=经过化简，式(7)转换成［11］

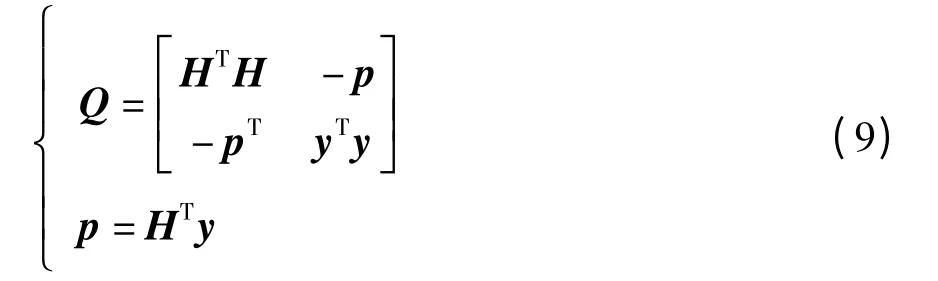
式(8)可由连续同伦投影并行下降法求解，称这种方法为QML-PSK 检测算法［11］.在给定矩阵Q后，其最大计算复杂度仅为O()，而其性能非常接近最大似然检测的最优性能［11］，因此，将QMLPSK 检测算法用于软解调，是一种在极低复杂度下逼近最优性能的求解思路.

在软解调中使用QML-PSK 检测算法的一大难题是如何将式(6)中的f(x)表示成式(8)中的二次型.当发射信号为QPSK 时，f(x)与式(7)中目标函数的差别仅为一线性项，将式(9)中的p 重新定义为p=HTy+σ2LA/2，得到

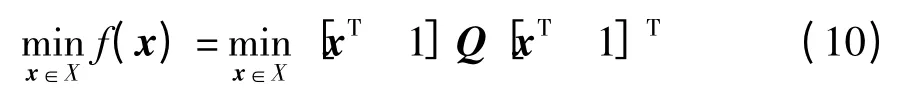
2.2 高阶QAM 星座图中的PSK 软解调算法

为降低高阶星座调制方式软解调方法的复杂度，文中利用比特级多流编码LST 传输技术将高阶星座分成数个调制能量不同的低阶星座，从而能够利用QML-PSK 检测算法进行软解调.不失一般性，文中以方形QAM 调制为例，其他形式的QAM 星座与此类似.

比特级多流编码分层调制是指编码比特映射到QAM 星座图上产生信号时，根据比特所代表信息的不同重要级别，在调制阶段将其分配到不同的能量层中.以16QAM 为例，其对应的4 阶脉冲幅度调制(4PAM)向量s(s∈{±1，±3}Nt)由MNt(M =2)个编码比特调制产生.根据信息的不同重要性，可以将这些编码比特按调制能量的不同分成两组，得到向量x2和x1(xi∈{±1}Nt，和分别为星座点xi的实部和虚部;i =1，2)，并由s =2x2+x1产生调制信号.16QAM 星座图的一种实现形式如图1 所示，Re 和Im 分别表示实轴和虚轴，调制能量高的比特x2决定了调制后信号所在象限，而调制能量低的比特x1决定了调制后的信号在象限中的位置.

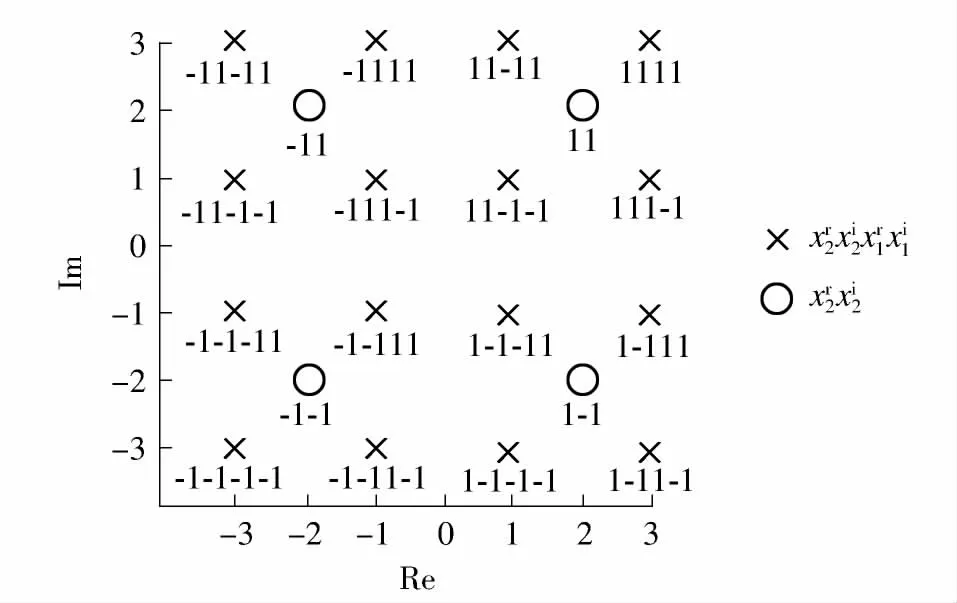
图1 比特级多流编码分层调制的16QAM 星座图Fig.1 16QAM constellation of bit-level multi-stream coded layered modulation

类似地，2McQAM 星座图对应的2MPAM 信号s可由M 个比特向量(xM，xM-1，…，x1)经过映射关系

调制得到，其中xi表示处于第i 层的所有比特，其调制振幅为2i-1.

通过定义矩阵W =［2M-1I 2M-2I … I］和向量，可将式(11)改写成矩阵形式:

从而高阶QAM 信号可以用BPSK 信号来表示.将式(12)代入式(4)中，得到QAM 星座图信号的统一表达式为

把HW 作为新的信道矩阵Hw，得到

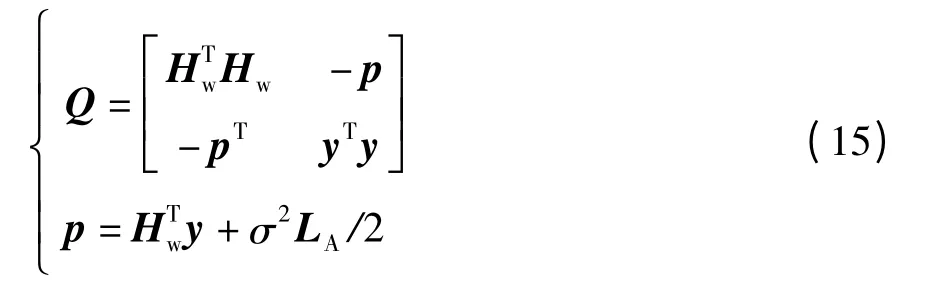
(1)由已知的y、H 和先验信息LA，根据式(12)、(13)将QAM 信号(见(4))改写成BPSK 信号形式(见(14));

(2)将式(14)代入式(7)，并利用式(15)将问题(7)等价转化，得到问题(10);

(3)采用QML-PSK 检测算法求解问题(10)，得到及

(4)将步骤(3)中所求结果代入式(6)，计算比特xk的外信息LE(xky).

虽然QAM-PSK 软解调算法具有复杂度低的优点，但对于高阶QAM 调制信号，直接根据式(10)和(15)计算外信息将导致误比特率(BER)随Turbo 迭代次数的增加而增加.这是因为根据式(6)、(10)及(15)计算比特xk的外信息LE(xky)时，使用了向量x 中所有其他比特的先验信息，即LA.然而，对能量(或比特信噪比Eb/N0)较高的编码比特进行解调时，使用能量(或Eb/N0)较低比特的先验信息会导致解调错误概率增大，这些错误在新一轮迭代中无疑会影响Eb/N0较高比特的解调性能.为避免上述问题，文中提出了一种适用于QAM-PSK 软解调算法的迭代接收机.

3 适用于QAM-PSK 软解调算法的迭代接收机

采用比特级多流编码分层调制及QAM-PSK 软解调算法的Turbo-MIMO 发射机和接收机模型如图2所示，其工作原理描述如下.

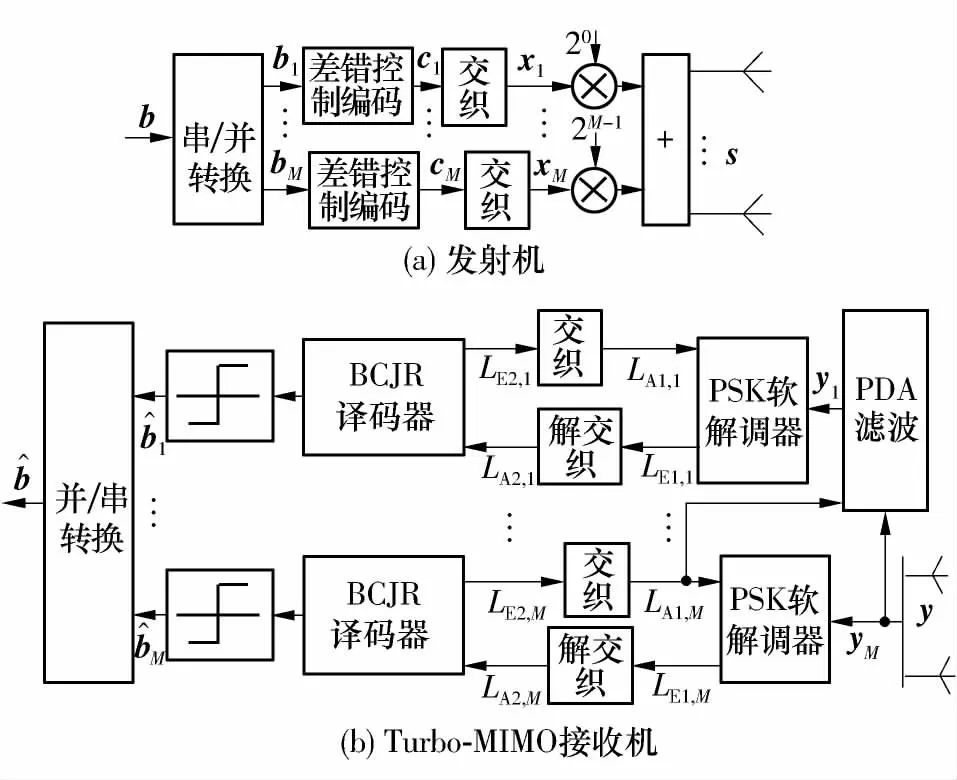
图2 比特级多流编码LST 收发机模型Fig.2 Model of bit-level multi-stream coded LST transceiver

在发送端，信息b 被分成M 个子流{bi，经过差错控制编码和交织后得到{xi，根据式(12)将M 个比特流{xi调制为PAM 符号流s，最后合成2 个PAM 符号流得到QAM 调制信号.

在接收端，在能量不同的层之间，迭代解调和译码按比特调制能量由高到低逐层进行.先由输入信号yM=y 对M 层比特流xM进行迭代解调和译码.当迭代次数达到上限时，由译码器输出编码比特软信息.第i(i ＜M)层根据上层比特软信息计算ni(ni=的均值i和方差，然后对y 进行概率数据关联(PDA)滤波［15］，得yi=(y-i)，再对xi进行迭代解调和译码.

需要指出的是，接收端每一层由QAM-PSK 软解调器和BCJR 译码器组成.对于软解调器，其输入由yi及xi的先验信息LA1，i组成，信号软解调后得到xi的外信息LE1，i，LE1，i经解交织后得到LA2，i;译码器将LA2，i作为编码比特ci的先验信息，译码得到外信息LE2，i，LE2，i经交织后得到更新的先验信息LA1，i，从而完成一次迭代.迭代次数达到上限后，由信道译码器的软输出判断信息bi的估计值i.

根据图2 所示的逐层解调结构可知，在解调能量较大的编码比特时可忽略能量较小比特的先验信息，从而将求解第i 层第l 个比特(xk=xi，l)的外信息计算公式修正为

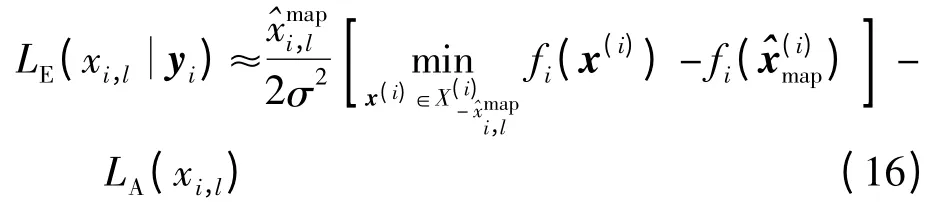
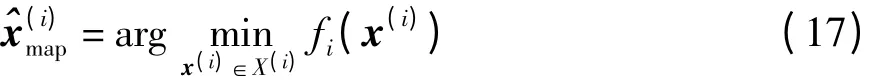
值得注意的是，由于优化问题的维数(即x(i)的维数iNt)随层数i 的减小而减小，求解LE(xiyi)的复杂度也会随i 的减小而不断下降.

Turbo-MIMO 接收机进行软信息迭代解调和译码的步骤如下:

(1)初始化LA1，i(t)=0，其中i=1，2，…，M;t=1，2，…，T;T 为发射所有编码比特的次数.

(2)i=M，yM=y.

(3)t=1.

(4)采用QML-PSK 算法求解式(17)，得到最优解(t)及函数值fi((t));对第i 层的所有得到外信息LE1，i(xi，l(tyi(t)).xi，l，求解式(16)中问题

(5)t=t +1，若t≤T，则转步骤(4)，否则转步骤(6).

(6)解交织{LE1，i(t)}Tt=1得到译码器先验信息LA2，i.

(7)采用BCJR 译码计算后验信息LD2，i和外信息LE2，i.

(8)若迭代次数达到上限，则由后验信息LD2，i硬判决得到估计值bi，并转步骤(10)，否则转步骤(9).

(9)LE2，i经交织器得到软解调的先验信息{LA1，i(t)}，转步骤(3).(10)若i ＞1，则i=i-1，计算，并转步骤(3)，否则输出

4 QAM-PSK 软解调算法的复杂度分析

对于文中所提的QAM-PSK 算法，分析求解x 中MNt比特外信息所需的复杂度.根据Turbo-MIMO接收机模型和式(16)，计算比特外信息需要求解和最优解，其中i=1，2，…，M;l=1，2，…，Nt.求第i 层的需使用PSK 检测算法求解Nti 维的优化问题，而求需使用PSK 检测算法求解维数为Nti-1 的优化问题Nt次，并且计算式(8)中Q 所需的复杂度为O(Nr).由于PSK检测算法求解K 维问题的复杂度为O(K2)，因而计算x 中所有比特外信息的复杂度为，当Nt=Nr时，其复杂度可近似为O(M3/3).

5 数值仿真

为验证所提QAM-PSK 软解调算法的性能，文中先通过仿真比较先验信息给定时QML-PSK 软解调算法与最优软解调算法的性能，然后比较QAMPSK 软解调算法与基于球形译码的LSD 算法［11］和SoD-HSD 算法［13］分别应用于软信息迭代接收时的误码率性能和复杂度.

与MAP 准则的最优性能相比，影响QAM-PSK软解调算法性能的因素包括Max-Log-MAP 近似和ML 检测中对整数约束的松弛.其中Max-Log-MAP近似的性能已有大量文献讨论［16-19］;当先验信息LA=0 时，将ML 检测中的整数约束松弛为复数恒模约束的性能在文献［11］中也有仿真验证.因此，文中主要比较当LA≠0 时将整数约束松弛为复数恒模约束的QML-PSK 软解调算法和性能最优的SoD-HSD 算法的性能.

考虑一个Tx发射天线和Tx接收天线的Turbo-MIMO 系统(Tx分别为4 和8)，信道为瑞利平坦衰落.数据帧长度为9216，数据总长度为500 帧.比特先验信息LA根据文献［7］计算:当比特xk及其与先验信息LA(xk)之间的互信息I 给定时，xk的先验信息LA(xk)为

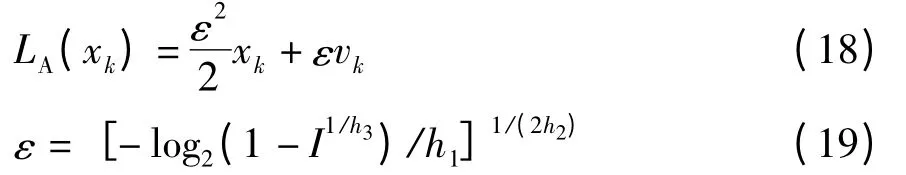
式中，h1=0.3073，h2=0.8935，h3=1.1064，vk是服从标准正态分布的随机变量.利用式(18)和(19)产生先验信息序列，再根据式(6)计算比特的外信息，便得到给定互信息时先验信息对软解调算法性能的影响.

在Max-Log-MAP 准则下，QML-PSK 软解调算法和最优SoD-HSD 算法［3］所输出的外信息随互信息的变化如图3 所示.仿真结果显示，QML-PSK 软解调算法的性能和最优SoD-HSD 软解调算法的性能非常接近，当互信息I ＞0.5 时，两者性能几乎一样.

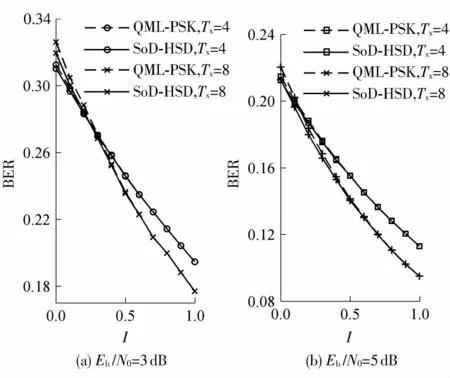
图3 外信息随互信息的变化Fig.3 Changes of external information with mutual information

参照文献［1］中的参数设置，考虑一个收发天线数均为8 的Turbo-MIMO 系统，其信道编码采用码率R =1/2、前馈和反馈多项式为(7，5)的并行Turbo 码，信道为瑞利平坦衰落.基于LSD 系统的数据帧交织长度为9 216，数据总长度为500 帧.对应的比特级多流编码分层调制及其QAM-PSK 软解调的系统参数如表1 所示，其中内迭代次数表示Turbo译码的迭代次数，外迭代次数表示解调器与译码器间的软信息迭代次数.

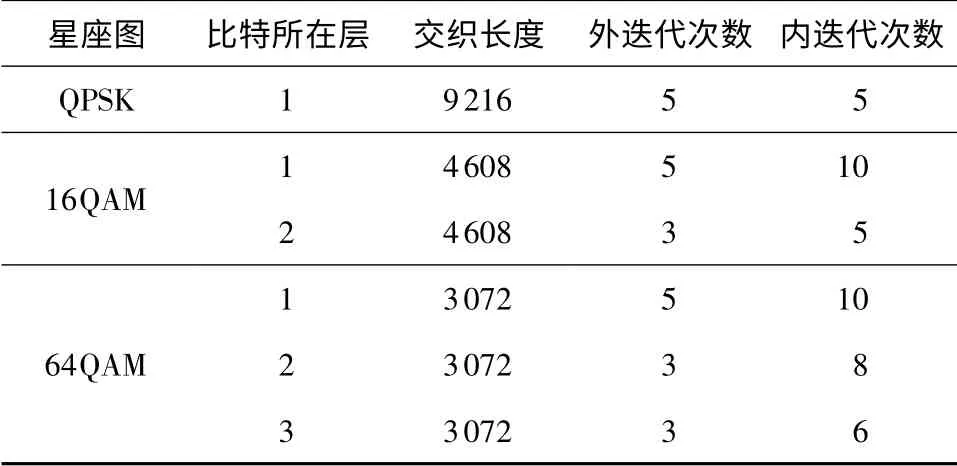
表1 基于QAM-PSK 的软解调迭代接收机的参数Table 1 Parameters of soft demodulation iterative receiver based on QAM-PSK

软信息迭代接收机使用不同软解调算法时的BER 性能随Eb/N0的变化如图4 所示，其中QPSK、16QAM 和64QAM 信号的容量限分别为1.6、3.8 和6.4 dB.对于QPSK 信号，3 种算法在BER =10-5时的比特信噪比几乎相同;对于16QAM 和64QAM 信号，基于QAM-PSK 软解调算法的系统的Eb/N0分别优于基于LSD 算法的系统约0.4 和0.3 dB，较基于SoD-HSD 算法的系统略大(约为0.1 dB).

图4 基于不同软解调算法的Turbo-MIMO 系统的BERFig.4 BER of Turbo-MIMO systems based on different soft demodulation algorithms

在与图4 相同的仿真条件下，QAM-PSK 软解调算法与LSD 和SoD-HSD 算法的平均运行时间之比如图5 所示.为比较不同解调算法的复杂度，仿真统计了接收机中软解调部分所消耗的时间.与基于球形译码的软解调算法相比，QAM-PSK 软解调算法的低复杂度优势在高阶QAM 星座中更为明显.在64QAM 中，当Eb/N0=12 dB 时，QAM-PSK 软解调算法的平均运行时间约为LSD 算法的1/4、SoD-HSD的1/2;当Eb/N0=9 dB 时，QAM-PSK 软解调算法与LSD 和SoD-HSD 算法的平均运行时间之比分别为1/80 和1/20.仿真结果表明，与基于SD 的软解调算法相比，QAM-PSK 软解调算法的低复杂度优势随调制阶数的增加和信噪比的减小而增大，显示出QAMPSK 软解调算法的复杂度较为恒定，而基于球形译码的软解调算法的复杂度在信噪比减小或问题维数增大时呈快速增加趋势.

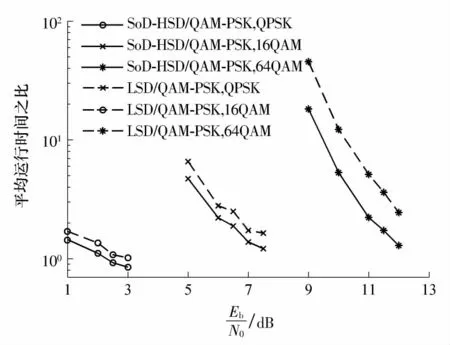
图5 不同比特信噪比下的平均运行时间之比Fig.5 Ratios of average running time at different bit SNRs

SoD-HSD 算法和QAM-PSK 算法的平均运行时间之比随天线数的变化如图6 所示，其中接收信号的信噪比为10 dB，发射天线数和接收天线数相同，其他参数设置与图4 相同.仿真结果显示，QAMPSK 算法在复杂度方面有着明显的优势，尤其是天线数较大时，其运行时间仅为SoD-HSD 算法的1/50.这进一步说明，当问题维数增加时，QML-PSK 算法的复杂度增加速度慢于基于球形译码的软解调算法.

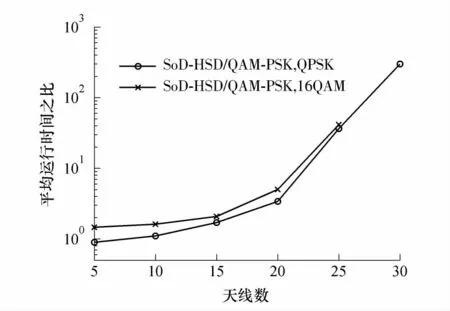
图6 SoD-HSD 和QAM-PSK 算法的平均运行时间之比Fig.6 Ratios of average running time of SoD-HSD to QAMPSK algorithms

6 结语

文中采用比特级多流编码LST 传输技术，将高效的QML-PSK 检测算法应用于Turbo-MIMO 无线通信系统的软信息迭代接收端中，提出了能广泛应用于各类QAM 星座图的QAM-PSK 软解调算法.在此基础上，为了在分层调制系统中避免低能量比特影响高能量比特的解调性能，提出了适用于QAMPSK 软解调算法的软信息迭代接收机，并分析了QAM-PSK 软解调算法应用于这种接收机时的计算复杂度.理论和仿真结果表明，文中提出的软信息迭代接收系统可以在较低的复杂度下逼近MIMO 信道容量限.当频率选择性衰落信道条件下的多用户系统存在码元间干扰和用户间干扰时，多用户的高效软解调问题以及实际系统中信道信息存在误差时的软解调算法，将是今后进一步研究的主要内容.

［1］Hochwald B M，ten Brink S.Achieving near-capacity on a multiple-antenna channel［J］.IEEE Transactions on Communications，2003，51(3):389-399.

［2］Haykin S，Sellathurai M，de Jong Y，et al.Turbo-MIMO for wireless communications ［J］.IEEE Communications Magazine，2004，42(10):48-53.

［3］Renqiu W，Giannakis G B.Approaching MIMO channel capacity with soft detection based on hard sphere decoding［J］.IEEE Transactions on Communications，2006，54(4):587-590.

［4］Kamruzzaman M M，Hao L.Performance of turbo-SISO，turbo-SIMO，turbo-MISO and turbo-MIMO system using STBC［J］.Journal of Communications，2011，6(8):633-639.

［5］Pei Xiao，Erik Ström.Soft demodulation algorithms for orthogonally modulated and convolutionally coded DS-CDMA systems［J］.IEEE Transactions on Communications，2010，58(3):742-747.

［6］李小玮，韦岗，陈芳炯.垂直分层空时码的迭代检测算法［J］.华南理工大学学报:自然科学版，2006，34(6):17-20.Li Xiao-wei，Wei Gang，Chen Fang-jiong.Iterative detection algorithm for V-BLAST［J］.Journal of South China University of Technology:Natural Science Edition，2006，34(6):17-20.

［7］Cai Shu，Matsumoto T，Yang Kehu.SIMO channel estimation using space-time signal subspace projection and soft information［J］.IEEE Transactions on Signal Processing，2012，60(8):4219-4235.

［8］Huang Yuheng，Dong Yan，Xie Rupeng，et al.A new rate adaptive system:controlled soft demodulation［C］∥Proceedings of ComComAp.Hong Kong:IEEE，2012:360-364.

［9］Steingrimsson B，Luo Zhi-quan，Wong K M.Soft quasimaximum-likelihood detection for multiple-antenna wireless channels ［J］.IEEE Transactions on Signal Processing，2003，51(11):2710-2719.

［10］Nekuii M，Kisialiou M，Timothy N D，et al.Efficient softoutput demodulation of MIMO QPSK via semidefinite relaxation［J］.IEEE Transactions on Signal Processing，2011，5(8):1426-1437.

［11］Kisialiou M，Luo Zhi-quan，Luo Xiao-dong.Efficient implementation of quasi-likelihood detection based on semidefinite relaxation［J］.IEEE Transactions on Signal Processing，2009，57(10):4811-4822.

［12］Jalden J，Ottersten B.An exponential lower bound on the expected complexity of sphere decoding［C］∥Proceedings of ICASSP.Stockholm:IEEE，2003:393-396.

［13］Kisialiou M，Luo Xiao-dong，Luo Zhi-quan.Semidefinite relaxation codes for the discrete integer least squares problem［EB/OL］.(2006-12-03)［2012-05-29］.http:∥www.ece.umn.edu/～luozq/Publication_Software.html.

［14］Bahl L，Cocke J，Jelinek F，et al.Optimal decoding of linear codes for minimizing symbol error rate［J］.IEEE Transactions on Information Theory，1974，20(2):284-287.

［15］Luo J，Pattipati K R，Willett P K，et al.Near-optimal multiuser detection in synchronous CDMA using probabilistic data association ［J］.IEEE Communications Letters，2001，5(9):361-363.

［16］Robertson P，Villebrun E，Hoeher P.A comparison of optimal and sub-optimal MAP decoding algorithms operating in the log domain［C］∥Proceedings of IEEE International Conference on Communications.Seattle:IEEE，1995:1009-1013.

［17］Perişoar˘a L A，Stoian R.The decision reliability of MAP，log-MAP，Max-Log-MAP and SOVA algorithms for turbo codes ［J］.International Journal of Communications，2008，1(2):65-74.

［18］Robertson P，Hoeher P，Villebrun E.Optimal and suboptimal maximum a posteriori algorithms suitable for turbo decoding ［J］.European Transactions on Telecommunications，1997，8(2):119-125.

［19］Vogt J，Finger A.Improving the Max-Log-MAP turbo decoder［J］.Electronics Letters，2000，36(23):1937-1939.