沃尔什序列组的两个新性质及其推论*

郭黎利 刘明夺 姜晓斐

(1.哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001;2.中国电子科技集团公司第54 研究所，河北 石家庄 050001)

沃尔什(Walsh)序列是一种正交性良好的伪随机序列.在理论数学和信息通信领域中，Walsh 序列得到了国内外很多学者的关注.文献［1］中介绍了Walsh 函数的一种变换形式;文献［2］中提出了一种新的生成能完全避免正交误差的Walsh 序列方法;文献［3-4］中给出了利用Walsh 序列特性变换来提高码分多址(CDMA)系统性能的算法;文献［5-6］中讨论了Walsh 序列的基本性质和生成算法;文献［7］中研究了Walsh 序列的均衡搭配性质，并在此基础上设计了一种新的Walsh 序列生成器.

文中在文献［5-7］研究的基础上，推导出完备Walsh 序列组中多条序列的列同性，依据列同性导出了2 个新推论，即完备Walsh 序列组中序列列同性的Walsh 编号关系及3 条序列等幅叠加生成序列和原序列组中序列的部分相关性，并进行了仿真验证.最后分析了叠加生成序列部分相关性在并行组合扩频(PCSS)通信系统四相相移键控(QPSK)调制中的应用，根据调制后正交序列和本地序列的部分相关性，采用峰值置零法来实现软判决接收，进一步扩展并行组合扩频通信系统多相相移键控(MPSK)软判决调制的实现方式.

1 Walsh 序列及其主要性质

Walsh 函数系是一种归一化完备正交函数系，有不同的定义方法和排列次序.文中应用的Walsh序列使用Walsh 编号排序，表示为Wal(l)，序列中第i 个码元表示为Wal(l，i)，其中l 为序列的Walsh编号，l=0，1，…，L-1;i =1，2，…，L;L 为Walsh 序列的阶数.Walsh 序列有很多重要的性质，文中仅介绍2 个主要的性质.

性质1 Walsh 序列的乘法定理［5］

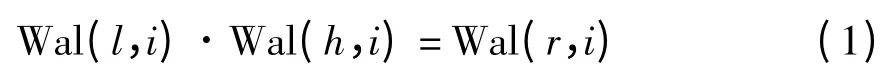
式中，r =l⊕h，即r 等于l 和h 的二进制表示式的模2 之和.

性质2 Walsh 序列的均衡搭配性质［7］

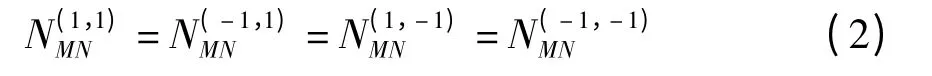
2 Walsh 序列的新性质及其推论

2.1 完备Walsh 序列组中3 条序列的列同性

性质3 在L ×L(L≥4)阶完备Walsh 序列组中，若从中选取任意不同序列Wal(a)、Wal(b)、Wal(c)，则此3 条序列中必有L/4 列码元完全相同，即满足

定义多条序列对齐后同列码元完全相同的情况为列同性.使用A、B、C 来代表序列Wal(a)、Wal(b)、Wal(c)，且a≠b≠c，其他序列表示方法与此类似.

证明 分3 种情况来讨论.

情况1 设a =0，则Wal(a，i)=1，其中i =1，2，…，L.根据Walsh 序列的均衡搭配性质(见式(2))，有

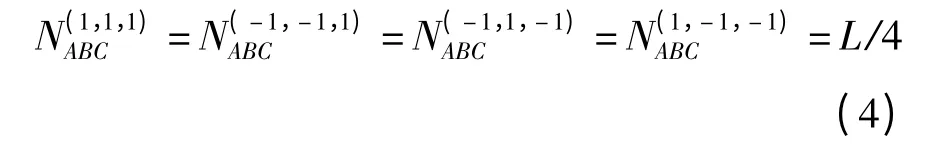
情况3 设a≠0，b≠0，c≠0，且a⊕b⊕c≠0.令f=a⊕bc，根据Walsh 序列的乘法性质可得

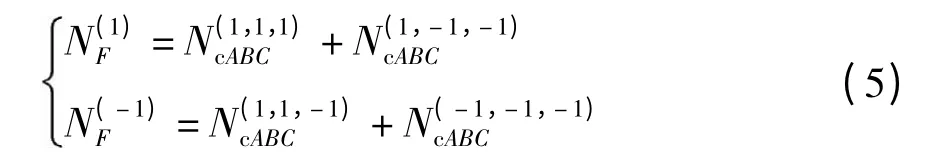
将式(6)代入式(5)，得

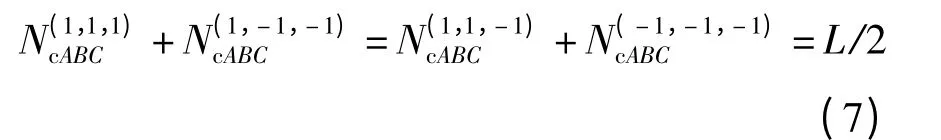
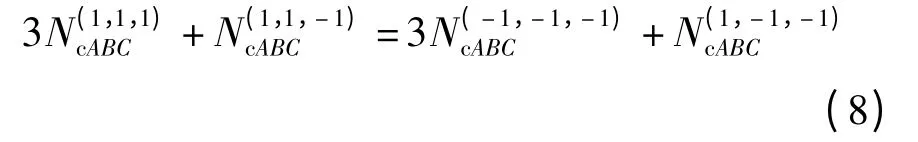
将式(8)代入式(7)，得到3 条序列的码元组合列数关系为

因RG(0)=RA(0)+RB(0)+RC(0)=3L，即

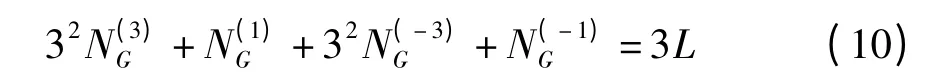
将式(10)代入式(7)、(9)，最终得到3 条序列的码元组合列数为

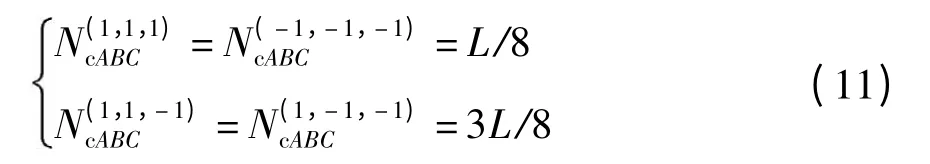
证毕.

2.2 完备Walsh 序列组中4 条序列的列同性

性质4 在L×L(L≥4)阶完备Walsh 序列组中，若从中选取任意3 条不同序列Wal(a)、Wal(b)、Wal(c)，则剩余组中必存在且仅存在1 条序列Wal(d)，使A、B、C、D 序列间有L/4 列码元完全相同，即满足

证明 分2 种情况来讨论.

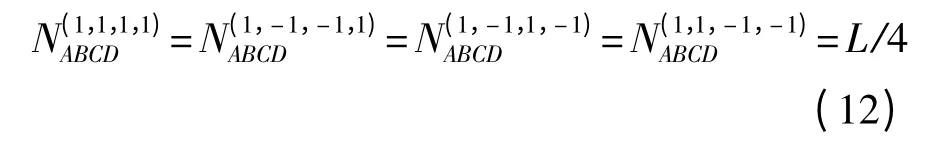
(2)若a≠0，b≠0，c≠0，a⊕b⊕c =0，这与(1)中题设条件相同，则4 条序列码元的组合列数为

(3)用反证法证明唯一性

假设完备Walsh 序列组中存在1 条序列E =Wal(e)，使A、B、C、D、E 间有L/4 列码元完全相同，a=0，b⊕c⊕d=0.

若A、B、C、D、E 有L/4 列码元完全相同，结合式(13)，则有=L/4.因b⊕c⊕e≠0，故根据式(11)可得

情况2 (1)若a≠0，b≠0，c≠0，且a⊕b⊕c≠0，则有3L/8.同时，设d=a⊕b⊕c，有

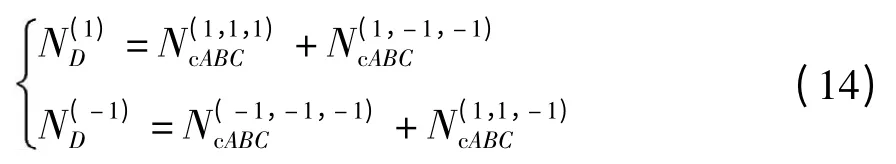
则序列A、B、C、D 的码元组合列数与序列A、B、C 的码元组合列数关系如下:

(2)用反证法证明唯一性

设完备Walsh 序列组中存在一条序列E =Wal(e)，使A、B、C、D、E 有L/4 列码元完全相同，即

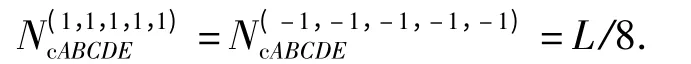
若e≠0，设H=A+B+C+D，则H 码元数为

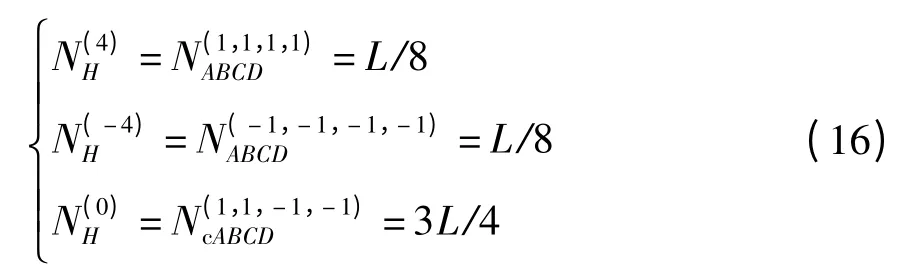
E 和H 的互相关函数为

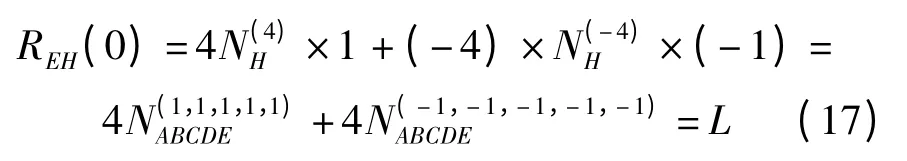
根据Walsh 序列间相关性，有REH(0)=0，而求得的REH(0)=L 与此矛盾，故Wal(e)不存在.证毕.

2.3 Walsh 序列列同性的Walsh 编号关系

推论1 在L×L(L≥4)阶完备Walsh 序列组中，若从中选取任意不同序列Wal(a)、Wal(b)、Wal(c)、Wal(d)，且这4 条序列之间有L/4 列码元完全相同，则其Walsh 编号满足a⊕b⊕c⊕d =0;在完备Walsh 序列组中，若任意4 条不同序列的Walsh 编号满足a⊕b⊕c⊕d=0，则此4 条序列之间有L/4 列码元完全相同.

2.4 等幅叠加Walsh 序列的部分相关性

推论2 在L×L(L≥4)阶完备Walsh 序列组中，若从中选取任意3 条不同的序列Wal(b)、Wal(c)、Wal(d)，令Z=B +C +D，将Z 按式(18)映射为2条正交的序列X 和Y(RXY(0)=0，xi、yi、zi分别表示序列码元):

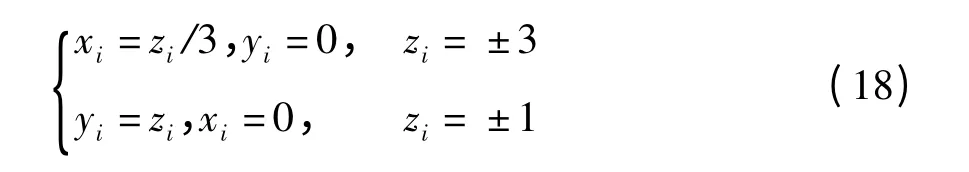
则X、Y 和剩余序列组中任意序列Wal(a)的相关函数有如下关系:

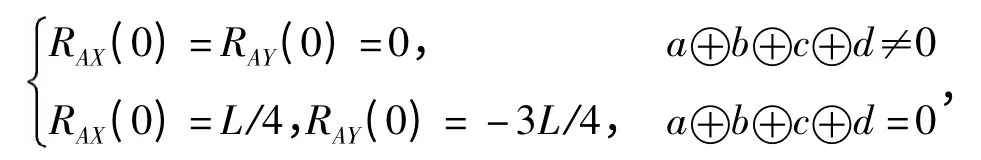
称此种相关性为完备Walsh 序列组中3 条序列等幅叠加生成序列和原序列组中序列的部分相关性.

证明 分3 种情况来讨论.情况1 和2 为a⊕b⊕c⊕d≠0 条件下的讨论，情况3 为a⊕b⊕c⊕d =0条件下的讨论.

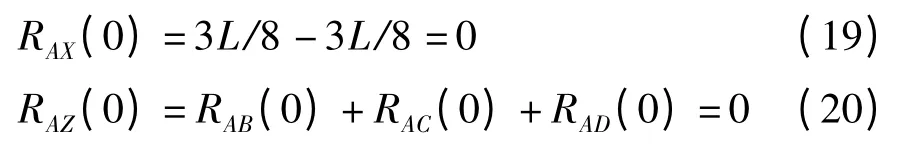
且

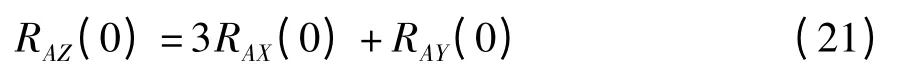
故RAY(0)=0.

情况2 设a≠0，b≠0，c≠0，d≠0，且a⊕b⊕c⊕d≠0，则根据性质3 和推论1 可知，必存在一条序列E=Wal(e).令B、C、D、E 有L/4 列码元完全相同，则b⊕c⊕d⊕e =0，且设P=B+C+D+E.

(1)若e=0，因N(4)P=L/4，N(0)P=3L/4，且A 和P 正交，则

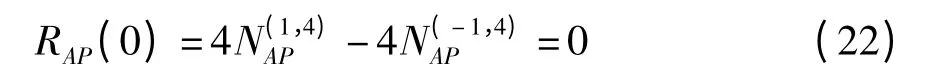
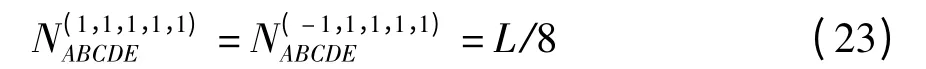
且有

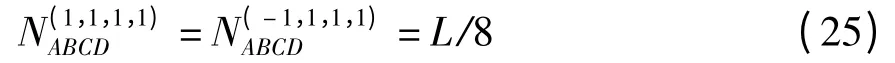
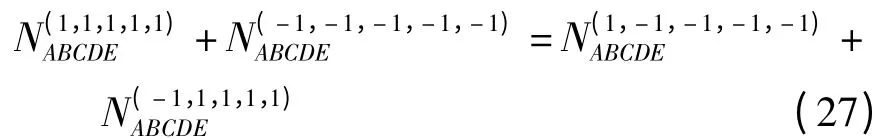
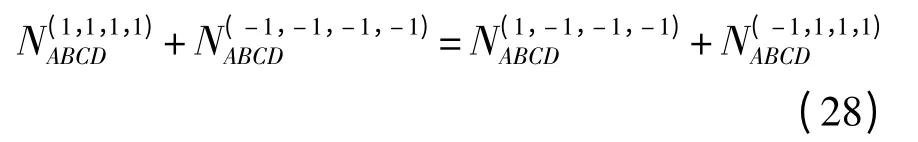
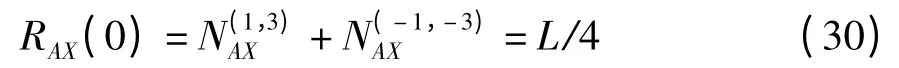
根据式(21)，有

证毕.

3 仿真结果验证

为验证完备Walsh 序列组中3 条序列等幅叠加生成序列的部分相关性，用Matlab 软件进行仿真，L=16 及L =32 时完备Walsh 序列组中等幅叠加序列Z 的部分相关性(ρXW(n)=RXWal(n)(0)/L 和ρYW(n)= RYWal(n)(0)/L，分 别 为RXWal(n)(0)和RYWal(n)(0)的相关系数)仿真结果如图1 所示.因为分别求Wal(n)与序列X 和Y 的相关值，所以每组数据得到2 幅子图.所选3 条序列的Walsh 编号分别根据推论2 证明过程中的2 种情况随机抽取.

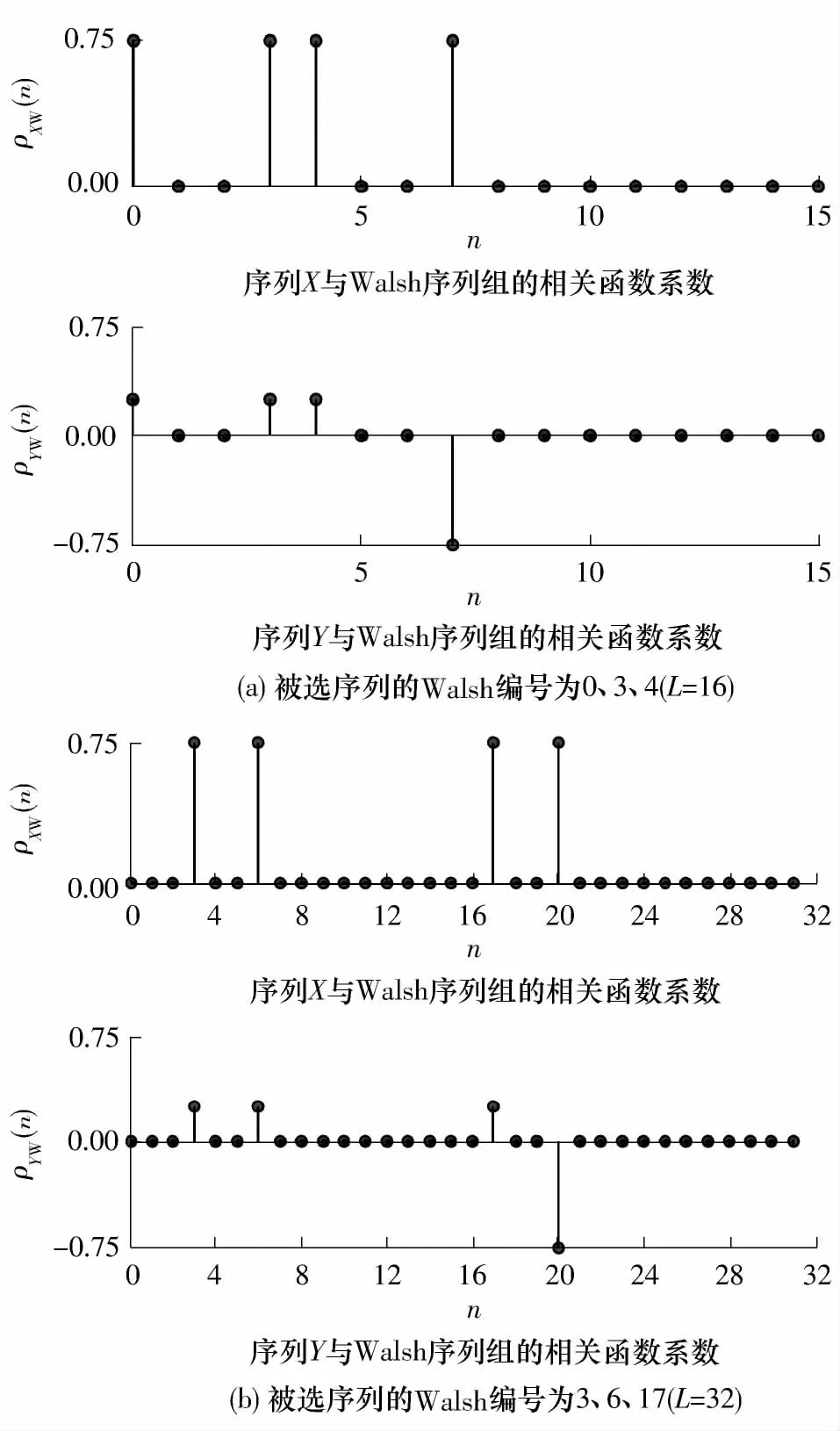
图1 完备Walsh 序列组中3 条序列等幅叠加生成序列映射后的部分相关性仿真结果Fig.1 Partial correlation simulation restults of three superposition sequences in complete Walsh sequence set

图1(a)中，映射后序列X、Y 和剩余组中任意编号为n(n ≠0，3，4，7)的序列正交，即ρXW(n)=ρYW(n)=0(n≠0，3，4，7).被选序列的Walsh 编号为0、3、4，则000⊕011⊕100 =111，即在完备Walsh序列组4 条序列列同性中第4 条序列的Walsh 编号应为7，故n=7 时，ρXW(7)=0.25，ρYW(7)=-0.75.

图1(b)中被选编号为3、6、17，在完备Walsh 序列组4 条序列列同性中第4 条序列的Walsh 编号应为20.可见，ρXW(n)=ρYW(n)=0(n≠3，6，17，20)，ρXW(20)=0.25，ρYW(20)=-0.75.

序列X、Y 和参与组成叠加序列的被选序列仍然保有自相关特性，且与其他序号满足a⊕b⊕c⊕d≠0 的序列正交，而与序号为d =a⊕b⊕c 的序列非正交，故称此序列Wal(d)为干扰序列.同时可以看出，干扰序列和X 的相关函数绝对值等于叠加序列与X 的自相关函数绝对值，Wal(d)和Y 的相关函数绝对值等于叠加序列与Y 的自相关函数值的3 倍.

4 叠加Walsh 序列部分相关性的应用

4.1 并行组合扩频通信系统模型

并行组合扩频通信系统在发射端每k 比特数据串并转换，然后送入数据序列映射器，在本地的M 个伪随机序列集{PNi}(i =1，2，…，M)中取出r 条不同的伪随机序列，同时考虑序列极性qi∈{0，-1，+1}，r 条序列并行传输形成组合序列，将该组合序列进行对应码片的等幅度叠加，形成多值叠加生成序列［8-10］

式中:qi为伪随机序列i 的选取控制因子，qi=0 表示不选取序列PNi，且qi=0 的取值共有M-r 个，qi= ±1 则表示选取序列PNi或序列PNi的互补形式;j=1，2，…，NT;NT为随机序列的周期长度.由于并行组合扩频通信系统中共有CrM 个序列选择状态，同时选取的r 条序列有2r个极性状态，数据序列映射方式为:依据从M 个扩频序列中选取的r 条序列的状态来映射k-r 比特数据，采用字典排序映射法［11-12］进一步根据这r 条扩频序列的极性完成r 比特数据的映射.每次发送的数据量k 可确定为

式中，［* ］表示对* 取整数部分.

接收端有M 个解扩器，在本地伪随机序列解扩之后，依据序列-数据逆映射算法，从M 个扩频序列相关器输出值中选出绝对值最大的r 个，结合它们的极性即可解调出原始发射信息［13-14］.

4.2 Walsh 序列在并行组合扩频通信系统QPSK 调制中的应用

在并行组合扩频通信系统中使用Walsh 序列作为被选序列，基带扩频后传输的是多值序列D(j)，D(j)共有r +1 种取值［15］，当M = L 且r =3时，多值序列D(j)的取值为{±1，±3}.

常规并行组合扩频信号QPSK 调制接收时只能通过硬判决来解调和解扩，即必须先解调判决出每个扩频码码元数据再进行解扩处理，性能无法达到最优.若按照文中推导的完备Walsh 序列组中3 条序列等幅叠加生成序列的映射关系，可实现系统的QPSK 调制软判决，即接收端解调时无需先判决出Walsh 序列中每个码元数据再解扩，而是可以同时进行解调解扩处理.

根据仿真分析可知，接收端的干扰序列Wal(d)和序列Y 的相关函数有如下特征:，若除去干扰序列，则可实现序列X、Y 与本地序列的完备正交.当Eb/N0=1 dB 时，应用图1(b)中序列实现并行组合扩频通信系统QPSK 置零软判决算法的接收端序列的相关系数如图2 所示.图2(a)、2(b)分别为I 和Q路解调解扩后的相关值，可见Q路中峰值RYD(0)为干扰序列，相对于其他相关值，干扰序列的相关绝对值较大，故可利用的峰值特性检测出Wal(d)的编号为20，将I 和Q 路中RXWal(20)(0)和RYWal(20)(0)同时置0，然后相加可得到图2(c)，则接收的多值序列与编号为3、6、17 的本地序列有较大的相关性，而与其他本地序列正交，即恢复了被选序列和原序列组中序列Wal(n)的完备正交性.

图2 采用QPSK 调制置零软判决算法的接收端相关系数Fig.2 Correlation coefficients of receiver using peak removal soft decision algorithm of QPSK modulation

进行上述处理后，从接收的M 组相关值中选择较大的r 个符号进行逆映射，完成系统信息的接收，实现并行组合扩频通信系统QPSK 软判决的解调.

5 结语

文中证明了在L ×L(L≥4)阶完备Walsh 序列组中，任意3 条序列对齐后有L/4 列同列码元完全相同，且在此序列组中必存在第4 条序列，使这4 条序列中有L/4 列同列码元完全相同.此3 条和4 条序列的列同性反映了完备Walsh 序列组内在的规律性，依据此性质推导出完备Walsh 序列组中4 条序列列同性的Walsh 编号的二进制之和为0，以及3条序列等幅叠加生成序列正交映射后2 条序列和原序列组中固定编号序列仍然正交.文中最后通过Matlab 仿真进一步验证了等幅叠加序列的部分相关性.

文中还简要分析了此生成序列的部分相关性在并行组合扩频通信系统QPSK 软判决调制的可行性，今后将进一步研究生成序列的部分相关性质在并行组合扩频通信系统中的其他应用.

［1］Falkowski B J，Rahardja S.Walsh-like functions and their relations［J］.Vision，Image and Signal Proceeding，1996，143(5):279-284.

［2］郭黎利，吴永梅，张晓林.产生Walsh 函数序列的一种新方法［J］.哈尔滨工程大学学报，2002，23(1):99-102.Guo Li-li，Wu Yong-mei，Zhang Xiao-lin.A new method of generating Walsh functional sequence ［J］.Journal of Harbin Engineering Unversity，2002，23(1):99-102.

［3］刘立程，胡瑞.利用沃尔什码扩频的MC-CDMA 系统频偏估计算法［J］.西安电子科技大学学报:自然科学版，2012，39(1):135-140.Liu Li-cheng，Hu Rui.Carrier frequency offset estimation algorithm in MC-CDMA systems with Walsh-code spreading［J］.Journal of Xidian University，2012，39(1):135-140.

［4］Choi Kwonhue，Liu Huaping.Quasi-synchronous CDMA using properly scrambled Walsh codes as user-spreading sequences［J］.Vehicular Technology，2010，59(7):3609-3617.

［5］胡征，樊昌信.沃尔什函数及其在通信中的应用［M］.北京:人民邮电出版社，1980:23-25.

［6］樊昌信.沃尔什函数应用研究之进展［J］.西北电讯工程学院学报，1977(3/4):8-33.Fan Chang-xin.The application development of Walsh function ［J］.Journal of Northwest Telecommunication Engineering College，1977(3/4):8-33.

［7］国佳，杨东凯，李署坚，等.基于均衡搭配性质的沃尔什函数生成方法［J］.北京航空航天大学学报，2009，35(7):848-851.Guo Jia，Yang Dong-kai，Li Shu-jian，et al.Generation method of Walsh function based on balanced matching property［J］.Journal of Beijing University of Aeronautics and Astronautics，2009，35(7):848-851.

［8］王玫，曹明，阳斌.短波并行组合扩频通信系统研究［J］.船舶电子工程，2009，29(11):79-82.Wang Mei，Cao Ming，Yang Bin.Study of HF parallel combinatorial spread spectrum systems ［J］.Ship Electronic Engineering，2009，29(11):79-82.

［9］Li Bei-ming，Guo Li-li，Qi Xiao-dong.Complex position code parallel combinatory spread spectrum communication system with FEC technique ［C］∥Proceedings of the 2009 WRI International Conference on Communications and Mobile Computing.Kunming:IEEE，2009:209-213.

［10］Jiang Xiaofei，Guo Lili，Wang Bailing，et al.Performance analysis for UWB system based on parallel combinatory spread spectrum using different pseudo noise sequences［C］∥Proceedings of the 2nd International Conference on Education Technology and Computer.Shanghai:IEEE，2010:213-216.

［11］Qi Lin，Guo Li-li，Jiang Xiao-fei.Performance studies of UWB communication system based on parallel combinatory spread spectrum［C］∥Proceedings of the 5th International Conference on Wireless Communications，Networking and Mobile Computing.Beijing:IEEE，2009:1-4.

［12］齐琳，郭黎利，姜晓斐.改进的并行组合扩频超宽带接收机性能［J］.北京邮电大学学报，2011，34(2):12-16.Qi Lin，Guo Li-li，Jiang Xiao-fei.A parallel combinatory spread spectrum based study on the improved UWB receiver［J］.Journal of Beijing University of Post and Telecommunications，2011，34(2):12-16.

［13］Liu Ming-duo，Li Hong-lei，Guo Li-li.Research of soft decision modulations based on parallel combinatory spread spectrum system ［C］∥Proceedings of the 5th Global Symposium on Millimeter Waves.Harbin:IEEE，2012:507-512.

［14］姜晓斐，郭黎利，齐琳，等.并行组合扩频超宽带系统的跳时多址接入方式［J］.华南理工大学学报:自然科学版，2011，39(9):115-119.Jiang Xiao-fei，Guo Li-li，Qi Lin，et al.Time-hopping multiple access performance of ultra-wideband system based on parallel combinatory spread spectrum ［J］.Journal of South China University of Technology:Natural Science Edition，2011，39(9):115-119.

［15］Liu Ming-duo，Guo Li-li，Li Hong-lei.BER performance of soft decision modulations based on PCSS system［J］.Journal of Harbin Institute of Technology:New Series，2013，20(2):134-138.