基于S变换的罗音信号检测算法*

李真真 吴效明

(华南理工大学 生物科学与工程学院，广东 广州 510006)

罗音是一种重要的异常呼吸音，也称为间断性音.通过检测罗音出现的时刻、个数、分布等特性，可提取肺部疾病的相关信息［1-3］.传统的罗音由医生听诊辨析，主观性强，易受外部因素的影响.自动化罗音检测更为客观稳定，是未来计算机辅助诊断领域的重要研究课题之一［4-5］.

当前罗音信号检测的主要方法有基于连续小波变换、小波包分解、小波网络等的方法，这类方法一般以小波重建中小波系数的异动来指示罗音的出现［6-8］.另外，还有基于经验模态分解的方法，经验模态分解法理论上比具有固定形态的小波更能体现罗音信号自身的特性，但仍欠缺固有模态函数与罗音特征的内在联系［9-10］.这些现有方法的主要缺点是将信号中的非平稳分量都判定为罗音信号，因此，信号中非罗音的非平稳分量(如摩擦音、心音等)会造成罗音检测的误判.基于分数阶希尔伯特变换的检测方法结合了罗音的非平稳特征与时域形态特征，避免了非罗音的非平稳分量的影响，取得了较高的罗音检测率［11］.但由于罗音信号随机性强、变异性大，仍然需要引入更新、更有效的信号处理方法以实现更稳定的罗音检测系统.

S 变换是由Stockwell 等［12］于1996 年提出的，是一种基于频率的时频分布变换，其在传统的短时傅里叶变换的高斯窗中引入了频率因子，使得该变换在高频处的窗口变窄，具有更高的时间分辨率，而在低频处的窗口变宽，具有更高的频率分辨率［12-15］.这一特性既可表征罗音信号在频域上的突变特征，又可表征罗音信号在时域上的形态特征.文中基于S 变换提出了一种罗音信号检测算法，并将该算法的实验结果与基于分数阶希尔伯特变换的算法进行了比较，以验证文中算法的有效性.

1 S 变换

S 变换是一种新的基于频率的时频变换方法，与短时傅里叶变换和连续小波变换密切相关.短时傅里叶变换STFT(，f)为

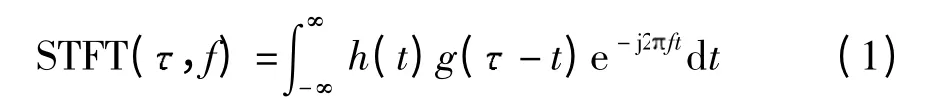
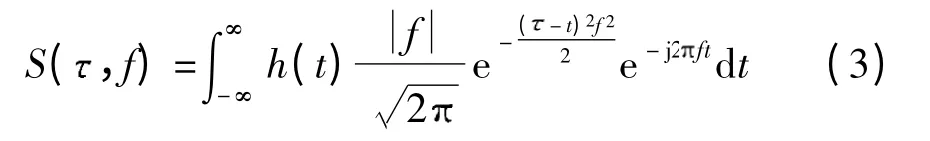
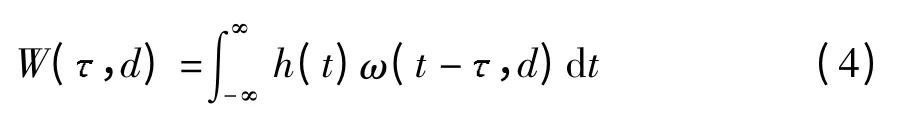
S 变换与连续小波变换的关系为

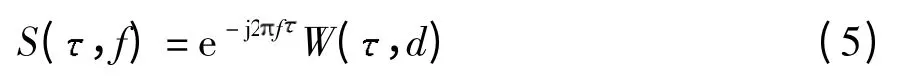
其中母小波ω(t，f)为

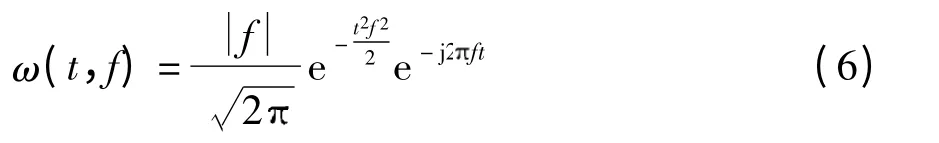
由于式(5)不满足小波的允许性条件，因此S变换不属于小波变换，但频率因子的作用使S 变换具有与小波变换类似的分析信号时间与频率局部变化的能力，可有效地从信号中提取出特征.

2 基于S 变换的罗音信号检测

2.1 呼吸音中的罗音

罗音是由闭合气道的突然不正常打开产生的，其持续时间一般小于20 ms，频率范围为100～2 000 Hz，时域波形起始于一个振荡，并逐步展宽.包含罗音信号的一段呼吸音信号如图1 所示，罗音信号检测就是要在罗音出现时将其从呼吸音信号中自动标记出来.

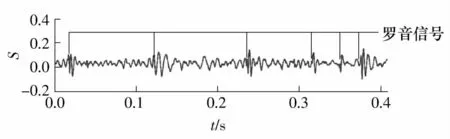
图1 呼吸音中实际罗音的波形示例Fig.1 Example of waveform of real crackles in respiratory sounds

2.2 仿真罗音信号的S 变换

罗音信号呈现特定形态，其时域基本形态可表示为仿真罗音信号

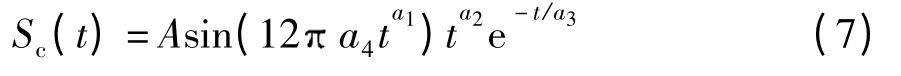
式中，a1=0.5，a2=1.49，a3=0.78，a4=2.0，A 为幅值因子.对仿真罗音信号做S 变换，考察罗音信号的时频域特征.

如图2(a)所示，在一段正常呼吸音中插入幅值因子分别为0.8 和0.6 的两个仿真罗音信号Sc(t).对信号做S 变换得到的时频谱图S(t，f)如图2(b)所示，谱图中存在两个高峰值区域，其频率范围大致为80～200 Hz，其时间轴上分别对应于两个仿真罗音信号;两个高峰值区域的能量强度与仿真罗音信号的幅值成正比，罗音信号的幅值小到与呼吸音信号背景相当(如幅值因子为0.6 的仿真罗音信号)时，S 变换的谱图中仍出现高峰值区.因此，可利用罗音信号对应于S 变换中的高峰值区域的特征进行罗音信号检测.在频率轴上对S 变换谱图做积分，可得J(t)，如图2(c)所示，对应于仿真罗音信号出现的时刻，J(t)也出现相应的峰值，可通过检测J(t)局部峰值实现罗音信号检测.

图2 仿真罗音信号的S 变换时频谱图Fig.2 S transform time-frequency spectra of simulated crackle signals

2.3 实际罗音信号检测算法流程

实际罗音信号检测的具体做法是:首先将肺音信号分为若干信号段，在每个信号段前加入一个参考的标准仿真罗音信号段构成测试信号段T(t)，对测试信号段做S 变换，得到相应的时频谱图S(t，f);接着去噪，去除谱图中能量较弱的成分，以突出谱图中的高峰值区域，得到^S(t，f);然后对^S(t，f)沿频率轴积分，得到随时间变化的谱图信号J(t);最后对局部峰值进行检测并标记罗音，得到检测结果R(t).设置标准仿真罗音信号参考段的关键作用在于维持S 变换时频谱图中的全局峰值水平，以排除小峰值群对检测判别的影响，标准仿真罗音信号幅值设定的准则是加入参考信号段前后待测信号段的总功率不变.以图1 中实际罗音信号为例，其检测流程及分步结果如图3 所示.

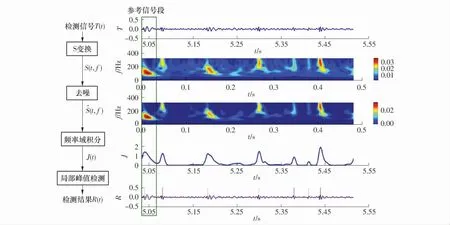
图3 实际罗音信号检测算法流程图Fig.3 Flowchart of detection algorithm of real crackle signals

3 实验仿真

采用2.3 节所述检测算法进行呼吸音中罗音信号的检测实验.呼吸音信号采用通用的美国胸科医学会教学呼吸音信号，实验采样率为11 kHz，对呼吸音信号随时间取5000 个采样点为一个检测信号段，并以50%叠加截取，共检测了4 组样本，检测结果如表1 所示.其中，正确检测出的信号段数为Nc，总检测段数为Nt，检测正确率ra=(Nc/Nt)×100%，正确检测出的罗音数为NTP，漏检的罗音数为NFN，误检的罗音数为NFP，敏感性指标SEN=NTP/(NTP+NFN)× 100%，阳性预测指标PPV = NTP/(NTP+NFP)×100%.

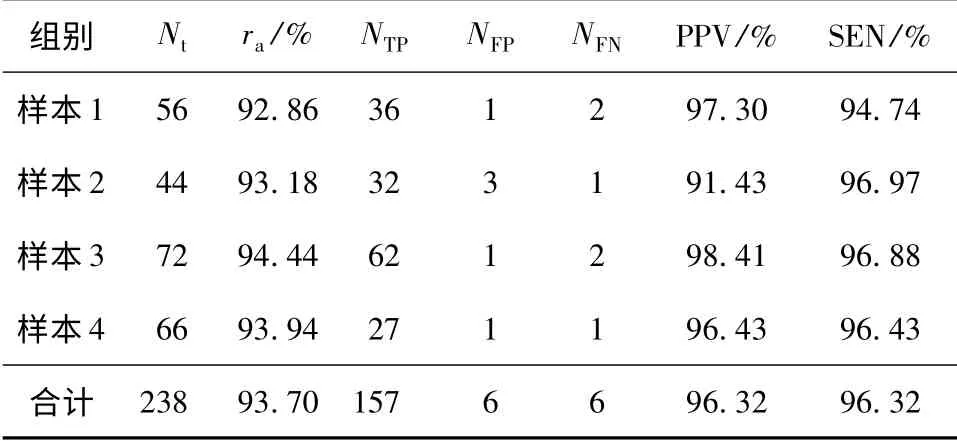
表1 文中算法的检测结果Table 1 Detection results of the proposed algorithm

可见，基于S 变换的罗音信号检测算法是有效的，检测正确率为93.70%，误判率与漏判率均为5.68%.产生漏判的主要原因是罗音信号的幅值较小且与幅值较大的罗音信号临近时，该段信号的局部峰值判别会受到幅值较大的罗音信号对应的峰值的影响.幅值较大的罗音信号的局部波峰会影响临近小幅值罗音信号的局部波峰的形态而导致幅值较小的罗音信号被漏判.若无大幅值罗音信号的干扰，则小幅值罗音信号仍可被检测到.如图4 所示的检测结果中，2 号罗音信号的幅值较小，受1 号罗音信号的影响而被漏判，3 号罗音信号实际上是由2 号罗音信号平移到该位置的，虽然2 号罗音信号未被检测到，形态幅值完全一致的3 号罗音信号却可被检测到.

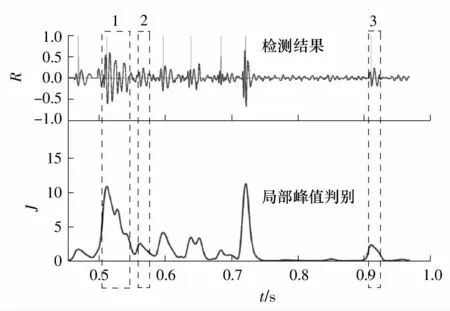
图4 罗音信号检测漏判情形示例Fig.4 Example of missing detection of crackle signal

产生误判的主要原因是存在形态类似罗音信号的非罗音信号，该信号在S 变换时频谱上的特征与罗音信号相似，易被误判为罗音信号.如图5 所示，误判的信号与罗音信号的形态类似，J(t)曲线也出现峰值，因此被误判为罗音信号.误判与漏判仍有改进的空间，在S 变换后的罗音信号特征提取中，J(t)单维积分未能充分提取二维S 变换谱图的特征信息，这有待进一步研究.

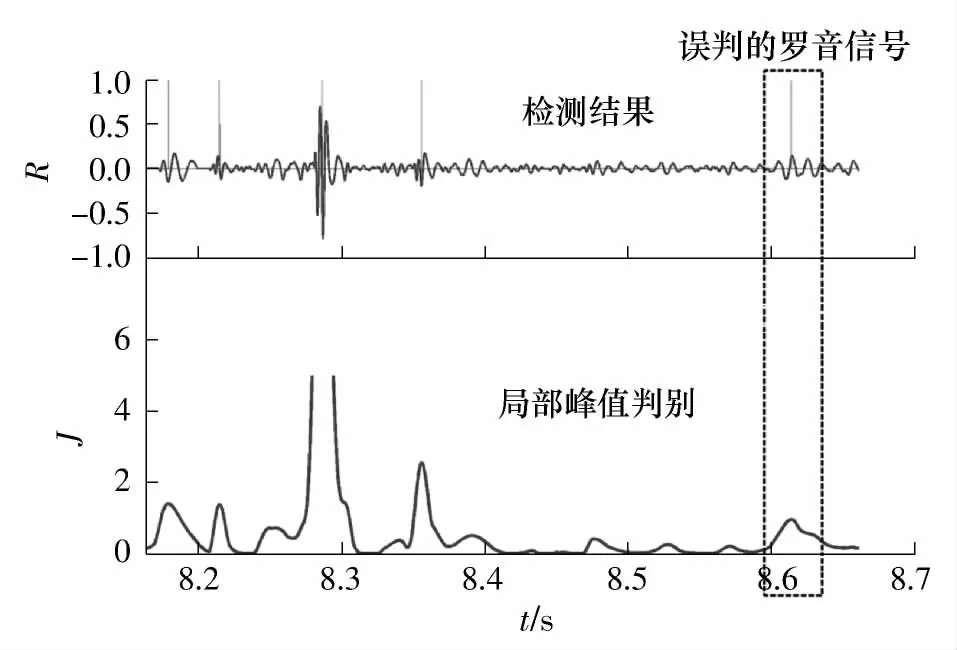
图5 罗音信号检测误判情形示例Fig.5 Example of false detection of crackle signal

罗音分为粗罗音与细罗音，其中频率较高的是细罗音.在4 组测试样本中，前2 组为粗罗音信号段，后2 组为细罗音信号段.在S 变换的时频谱图中，也体现了细罗音信号的频率更高的基本特性，如图6 所示，前两个粗罗音信号的局部高峰区对应的频率范围为100～300 Hz，后两个细罗音信号的局部高峰区对应的频率范围为200～800 Hz;另外，从峰值区域的形态上看，粗罗音信号对应的峰值区域更宽更扁，而细罗音信号对应的峰值区域更为细长.粗细罗音信号所反映的疾病类型不同，其分类具有一定的临床意义，因此，进一步的研究中，可依据粗细罗音信号在S 变换时频谱图上的峰值区域形态特征进行罗音分类.

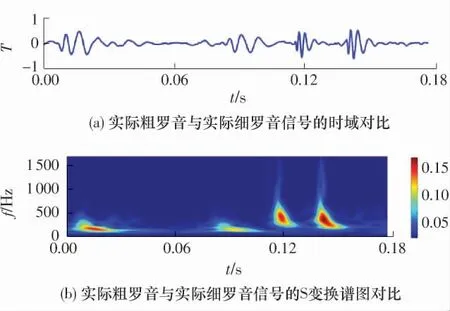
图6 粗细罗音信号S 变换时频谱图的对比Fig.6 Comparison of S transform time-frequency spectra between coarse and fine crackle signals

由于罗音信号的随机性强，变异性大，检测样本对检测结果的影响较大.现有检测算法的正确率一般在90%以上，其中基于小波变换的检测算法的正确率在90%～95%之间.采用前面4 组测试样本进行实验，基于分数阶希尔伯特变换的罗音信号检测算法的检测正确率为91.20%，误判率为6.40%，漏判率为2.80%，显然，文中算法对误判的情形有所改善.此外，文中算法的计算速度比基于分数阶希尔伯特变换的算法快，这是由于分数阶希尔伯特变换受到信号长度的影响，每次只能计算500 个采样点，每阶希尔伯特变换计算的数量级为0.1 s，10 阶以上的希尔伯特变换的计算时间已达1 s，而文中算法每次计算5000 个采样点，整个算法的计算时间的数量级也仅为1 s.

4 结语

文中提出了一种基于S 变换的时频谱图特征提取的罗音信号检测算法.先对含罗音的呼吸音信号做S 变换，再对S 变换的时频谱沿频率轴积分，降维得到一维特征曲线并做局部峰值检测，即可得到最终的自动检测结果.实验结果表明，S 变换优越的时频分辨性能可有效地提取罗音信号信息，该算法的检测效果优于现有的检测算法.

S 变换时频谱图降维方法未能充分提取到罗音信号的特征信息，因此，由S 变换检测罗音信号的方法仍有提升的空间，可进一步研究从S 变换时频谱中提取与罗音信号相对应的二维特征的方法.另外，粗细罗音信号在S 变换时频谱图中也表现出一定的差异，可根据提取的二维特征进行粗细罗音分类.

［1］Reichert S，Gass R，Brandt C，et al.Analysis of respiratory sounds:state of the art［J］.Clinical Medicine:Circulatory，Respiratory and Pulmonary Medicine，2008，2:45-58.

［2］Marques A，Bruton A，Barney A.The reliability of lung crackle characteristics in cystic fibrosis and bronchiectasis patients in a clinical setting［J］.Physiological Measurement，2009，30:903-912.

［3］Gavriely N.Breath sounds methodology ［M］.Boca Raton:CRC Press，1995:18-22.

［4］Sovijarvi A R A，Vanderschoot J，Earis J E.Standardization of computerized respiratory sound analysis［J］.European Respiratory Review，2000，10(77):585.

［5］Charbonneau G，Ademovic E，Cheethanm B M G，et al.Basic techniques for respiratory sound analysis［J］.European Respiratory Review，2000，10(77):625-636.

［6］Hadjileontiadis L J，Panas S M.Sepatation of discontinuous adventitious sounds from vesicular sounds using a waveletbased filter［J］.IEEE Transactions on Biomedical Engineering，1997，44(12):1269-1281.

［7］Lu X，Bahoura M.An integrated automated system for crackles extraction and classification［J］.Biomedical Signal Processing and Control，2008，3(3):244-254.

［8］Yeginer M，Kahya Y P.Feature extraction for pulmonary crackle representation via wavelet networks［J］.Computers in Biology and Medicine，2009，39(8):713-721.

［9］Sonia C，Ramon G，Tomas A.Crackle sounds analysis by empirical mode decomposition［J］.IEEE Engineering in Medicine and Biology Magazine，2007，26(1):40-47.

［10］Li Z Z，Du M H.HHT based lung sound crackle detection and classification［C］∥Proceedings of International Symposium on Intelligent Signal Processing and Communications Systems.Hong Kong:IEEE，2005:385-388.

［11］李真真，杜明辉，吴效明.基于分数阶希尔伯特变换的罗音特征提取［J］.华南理工大学学报:自然科学版，2011，39(12):38-42.Li Zhen-zhen，Du Ming-hui，Wu Xiao-ming.Crackle feature extraction based on fractional Hilbert transform［J］.Journal of South China University of Technology:Natural Science Edition，2011，39(12):38-42.

［12］Stockwell R G，Mansinha L，Lowe R P.Localization of the complex spectrum:the S transform［J］.IEEE Transactions on Signal Processing，1996，44(4):998-1001.

［13］Pei S C，Wang P W.Discrete inverse S transform with least square error in time-frequency filters ［J］.IEEE Transactions on Signal Processing，2010，58(7):3557-3568.

［14］Robert A B，Lauzon L M，Richard F.A general description of linear time-frequency transforms and formulation of a fast，invertible transform that samples the continuous S-transform spectrum nonredundantly ［J］.IEEE Transactions on Signal Processing，2010，58(1):281-290.

［15］Suja S，Jerome J.Pattern recognition of power signal disturbances using S-transform and TT transform［J］.International Journal of Electrical Power ＆ Energy Systems，2010，32(1):37-53.