PAMF处理的抗混响应用仿真研究＊

夏 雪 张明敏 王平波

（海军工程大学水声电子工程系 武汉 430033）

0 引 言

随着现代主动声呐体制向低频化、大功率、大孔径方向发展，混响作为声呐主动工作方式下特有的干扰，对水声信号检测性能的影响日趋凸显.而对于载体运动的主动声呐来说，混响的一个重要特征便是由平台运动引起的多普勒扩展.这种扩展与机载预警雷达的杂波谱扩展特性非常相似，所以运动声纳混响的抑制可以借鉴发展较为成熟的雷达杂波抑制技术.

1973年，Brennan首先提出了空时二维杂波处理思想并用于机载雷达，其实质就是将一维空域滤波技术推广到时间与空间二维域中.实际上，机载预警雷达面临的杂波环境往往是非均匀的［1］，因此非均匀环境下的空时自适应处理（STAP）方法受到越来越广泛的关注.近年来提出的参数自适应匹配滤波法PAMF［2－4］是一种与传统空时自适应处理结构完全不同的新方法，可称为线性预测类空时自适应处理方法［5］.

本文从匹配滤波的的角度，对空时最优处理器和PAMF处理器进行比较详细的对比，分析了PAMF处理器的原理、结构以及性能，并指出在小样本数情况下PAMF处理器检测信号的优势，并分析这种优势产生的原理.

1 空时最优处理的匹配滤波解读

考虑均匀线列阵的一组输出序列：｛x（m）｜m＝0，1，…，M－1｝，x（m）∈CN×1，M 为采样时间点数，N为阵元数，如果干扰信号xu是高斯分布的，则最优空时处理器的权矢量可以表示为：

式中：γ为任意标量，不失一般性，取γ＝1；Ru＝是干扰协方差矩阵；e∈CMN×1为目标的空时导向矢量，可表示为

式中：⊗为Kronecker积；fd为归一化时间导向矢量；fs为归一化空间导向矢量，则空时最优处理器的输出为

也可以从匹配滤波的角度来理解空时最优处理器，这时可称为MF处理器，即匹配滤波处理器.由于Ru是一个正定厄米特矩阵，所以可以对其做LDU分解得到

式中：A∈CMN×MN为一个下三角矩阵，其主对角线上是M个单位矩阵IN；D∈CMN×MN是一个块对角矩阵，主对角线上的元素为D（m）∈CN×N，m＝0，1，…，M－1.

即为空时最优滤波器的匹配滤波形式.其中A－1为块白化滤波器，而为联合方差归一化滤波器，MF处理器结构见图1.

图1 MF处理器结构框图

令Rε（m）＝E｛ε（m）ε（m）H｝为预测误差协方差矩阵，该矩阵为正定厄米特矩阵，对其做LDU分解得

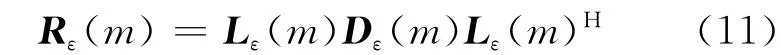
式中：Lε（m）为一个下三角矩阵；Dε（m）为一个对角线矩阵，令T（m）＝（m），PAMF处理器结构见图2［6］.

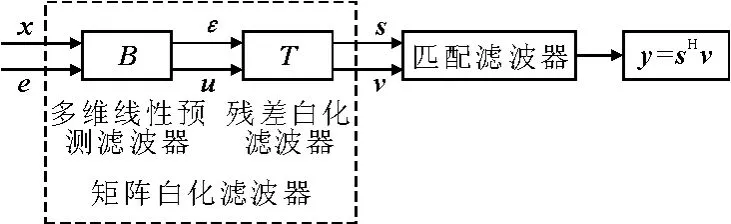
图2 PAMF处理器结构框图

PAMF方法利用固定的阶数和模型参数来设计多维线性预测误差滤波器和残差白化滤波器，大大简化滤波器设计过程，以上就是PAMF处理器的原理和结构.

PAMF处理器设计的关键在于求取多维线性滤波器系数，根据不同的准则有不同的求取方法，这里采用最小二乘法.

2 PAMF处理器设计

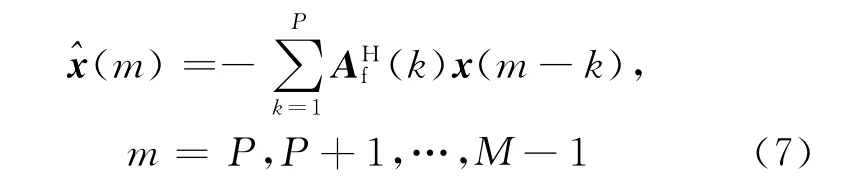
则前向线性预测误差为

式中：Af（0）＝IN，为简便起见，把计数起点由P改为0，并用一种更加紧凑的形式表示.

式中：

最小二乘法的目标是求得使最小的预测系数Af（p），k＝1，…，P，为此要解如下方程：

由于解方程的过程相当复杂，因此只给出结果［7］：

式中：Rff∈CPN×PN和Rf1∈CPN×N是矩阵Rf∈CP（N＋1）×P（N＋1）的子阵，关系如下.

以上即为PAMF处理器的设计过程原理、结构及设计过程.

3 抗混响应用仿真实例

1） 仿真条件 仿真环境见图3.

图3 实验仿真环境

仿真实验采用如上混响仿真软件.海底海面和体积散射源个数分别为：2 000，4 000和6 000，海底地质为泥沙底质；风速为6kn，体积散射强度为－75dB，接收放大倍数为60dB.平台速度10kn，接收阵为115的ULA，阵元间距1个半波长，摆放位置为正侧视阵；发射单频信号频率为750Hz，脉宽为0.1s；目标方位为60°，径向速度为－5kn（实际速度为10kn）；信混比为0dB，噪混比为－20dB.目标与接收阵的相对位置见图4.

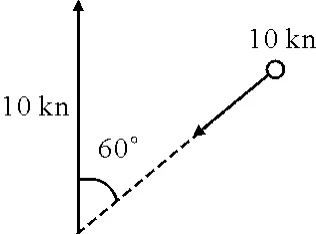
图4 仿真示意图

2） 原始接收信号 接收阵列某一路输出见图5.

图5 某一阵元通道接收信号幅度图

由上图，并不能从接收信号的波形得到目标信息，需经过处理.

3） 目标检测性能 仿真条件如上述，当训练样本数为80，时间序列长度为120时，仿真结果见图6～7.

图6 MF检测结果（样本数为80）

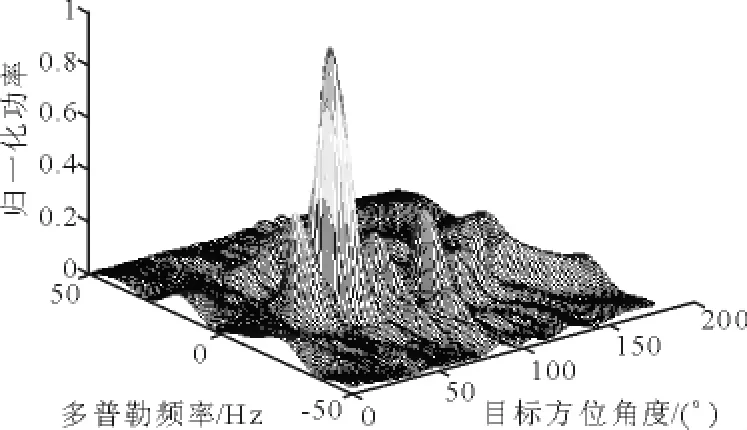
图7 PAMF检测结果（p＝5，样本数为80）

目标的多普勒频率可由以下公式计算得到

式中：va为目标与平台的相对速度；c为声速；f0为发射信号频率，根据该公式可计算目标多普勒：

由以上2图比较发现，在样本充足的情况下，MF算法对干扰的抑制效果较PAMF方法好，但是二者差别不大.

在以上样本数充足的条件下，两种处理器的处理结果相差不大，样本数降低到20时的处理结果见图8～9.

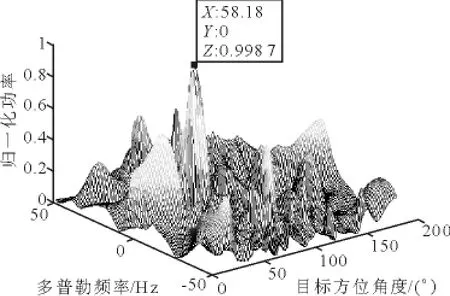
图8 MF检测结果（样本数为20）

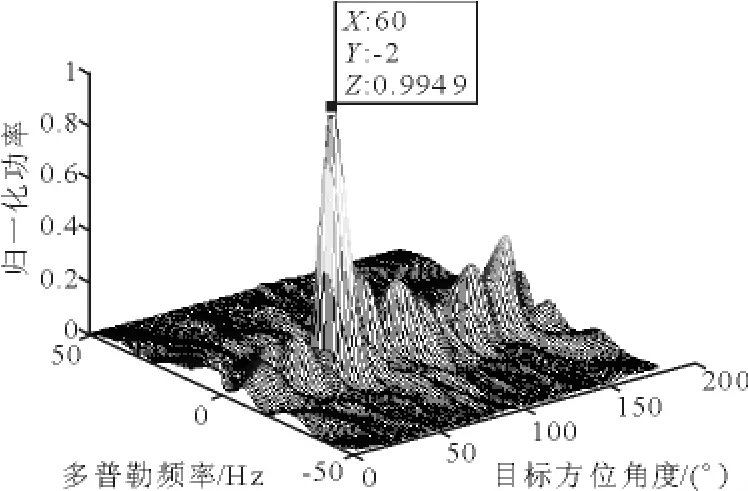
图9 PAMF检测结果（p＝5，样本数为20）

由上图可见，在小样本数情况下，MF的检测效果远不及PAMF.在MF处理器的处理结果中不仅有很多干扰未得到有效抑制，并且对目标的方位和多普勒估计不准确.而PAMF处理器的处理结果与大样本数条件下并无很大差别，目标依然清晰可见.究其原理，下一小节将进行阐述.

4 仿真结果原理解释

一个声呐信号检测系统，只有当系统的自由度大于混响自由度的时候，才能准确地对目标进行估计.而混响的自由度可以由以下公式近似估算出：

式中：N为阵元数；β为归一化多普勒角频率和归一化空间角频率的比值；M为时间序列的长度.实际上，混响的自由度往往比用上式估计出来的值高，这时可以通过观察采样协方差矩阵的大特征值来判断混响自由度.Ru的特征值谱见图10.

图10 MF处理器中＾Ru的特征值谱

而PAMF处理器在低样本数条件下依然能保持较好的目标检测性能是因为，PAMF处理器中多维线性预测滤波器的系数Af（k）是由＾Rf而不是估计得到的，在不同的预测阶数p下的特征值谱如图11所示.

图11 PAMF处理器中＾Rf的特征谱

5 结束语

本文描述了PAMF算法的原理、结构、设计过程以及在小样本数条件下检测目标的优越性，从检测结果和处理器内部机构论证了这种优越性并解释了其产生的原因.由于声呐信号处理往往是处于非均匀环境，因此可用的训练样本数有限，而PAMF算法在小样本数条件下依然具有很好的检测性能这一特性适合运用于非均匀环境下的信号检测，是一种值得深入研究应用的信号检测处理器.

［1］王永良，彭应宁.空时自适应信号处理［M］.北京：清华大学出版社，2000.

［2］MICHELS J H，HIMED B，RANGASWAMY M.Evaluation of the normalized parametric adaptive matched filter STAP test in airborne radar clutter［C］∥IEEE International Radar Conference，Washington DC，2000：769－774.

［3］ROMAN J R，RANGASWAMY M，DAVIS D W，et al.Parametric adaptive matched filter for airborne radar applications［J］.IEEE Trans AES，Apr 2000，36（2）：678－692.

［4］MICHELS J H，ROMAN J R，HIMED B.Beam control using the parametric adaptive marched filter STAP approach.In IEEE Radar Conference［J］.Huntsville，Alabama，May 2003，405－412.

［5］吴 洪，王永良，武 文.非均匀杂波环境下线性预测类空时自适应处理性能分析［J］.自然科学进展，2007，17（1）：86－92.

［6］詹昊可.主动声呐空时混响抑制方法研究［D］.武汉：海军工程大学，2008.

［7］DONG Yuhan.Parametric adaptive matched filter and its modified version［J］.Institution of Electrical Engineers，2006（11）：5－30.