钢管混凝土拱桥动力特性测试*
2013-08-18唐小兵
胡 钢 唐小兵
(黄冈市建设工程质量监督站1) 黄冈 438000) (武汉理工大学交通学院2) 武汉 430063)
0 引 言
钢管混凝土拱桥具有自重轻、强度大、抗变形能力强等优点,比较好地解决了修建桥梁所需求的用料省、安装重量轻、施工简便、承重能力大的诸多矛盾,是大跨度拱桥的一种比较理想的结构形式[1].钢管混凝土拱桥的静力性能研究已经比较成熟,动力性能的研究则起步较晚,而桥梁结构的动力特性(频率、振型和阻尼比)是桥梁承载力评定的重要参数之一,由于钢管混凝土拱桥抗振性能、车振性能等具有其自身的特点,这就使得钢管混凝土拱桥动力分析研究显得非常重要.
文中介绍了桥梁动力特性测试的基本原理,比较了环境随机激振法与自由衰减振动信号谱分析法(或冲击法)的特点,然后对常用激振方法及钢管混凝土拱桥动力特性测试时传感器布置等问题进行了讨论.
1 动力特性测试基本原理
结构动力特性即结构固有频率、振型与阻尼比的测量,属于结构动力学求解3大问题中的系统识别问题,即已知系统的输入和输出,确定系统的特征参数.
这些参数的测量传统方法是采用实测传递函数或频率响应函数来进行,但对于大型桥梁结构,一般激振设备不能提供足够的能量来激起桥梁的振动,即不能通过桥梁的输入(激励)和输出(响应)得到传递函数.
为了获得结构的固有频率、振型与阻尼比等参数,文献[2]介绍了自由衰减振动信号谱分析法,文献[3]介绍了脉动法或称环境随机激振法.
实际上,由随机振动理论[4-5],对于单自由度线性系统或者多自由度线性系统的单输入单输出情况,有

式中:Sxx(ω)和Szz(ω)分别为激励x(t)和响应z(t)的自功率谱密度函数;H(ω)为系统对应于激励和响应的频率响应函数,激励和响应均可以是位移、速度、加速度或力等任何物理量.
在桥梁动态特性参数测量中,传感器常用位移式、速度式或加速度式,其中用得最多的是加速度传感器,而位移y(t)、速度)和加速度t)响应的自谱密度函数之间满足

式(1)与式(2)表明,只要获得位移、速度和加速度响应的自谱密度函数中的任何一个,并且知道激励的自谱密度函数,就可以得到系统的频率响应函数.
就环境随机激振法而言,激励x(t)的自谱密度函数Sxx(ω)可以视为白噪声谱,即在感兴趣的宽频带内有Sxx(ω)=S0=常数.从式(1)可见,通过响应的自谱密度函数Szz(ω)可以得到系统的频率响应函数 H(ω),而且Szz(ω)的峰值就是H(ω)的峰值,由此可以识别出系统的固有频率.
对于自由衰减振动信号谱分析法,可以采用载重汽车跳车激起桥梁振动,然后测量各测点自由衰减振动响应.跳车激励实际上是一个脉冲函数^F·δ(t),而脉冲函数的自相关函数仍然为脉冲函数,自相关函数为脉冲函数的自谱密度函数则是一常数.以单位脉冲函数δ(t)考虑,有
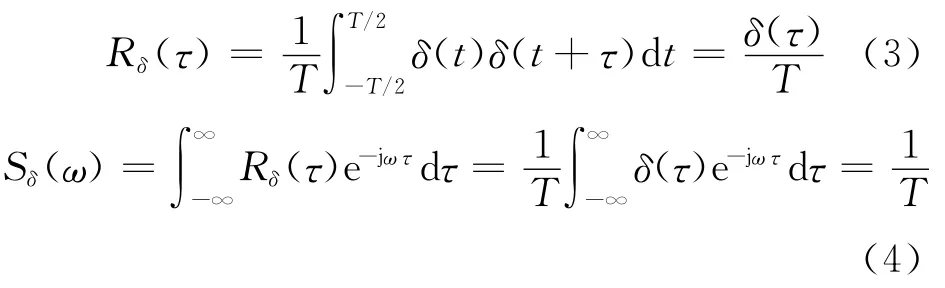
上述分析说明,自由衰减振动信号谱分析法与环境随机激振法从本质上来说是同一方法,它们的激励信号自谱密度函数在较宽的频带内均为一常数.然而,两者又有着很大的不同之处:自由衰减振动是由跳车激励引起的桥梁自由振动,其信号会很快衰减,测试时间比较短;而环境随机激振法则需要足够长的测试时间,以保证激励信号的自谱密度函数是一常数.因此,环境随机激振法比较适合没有通车的新建桥梁的动态特性参数测试或桥梁结构长期健康监测,而自由衰减振动信号谱分析法则非常适合桥梁封闭时间不能太长特别是已通车的高速公路桥梁动态特性参数测试.
对于振型的识别,如果系统各阶固有频率相距较远,且阻尼比很小,那么在第r阶固有频率附近,第r阶模态对自由衰减振动响应的贡献是主要的,由文献[2]的式(5)或式(6),若采用的是位移传感器,有

式中:ZA(fr)与ZR(fr)分别为位移测点 A 与参考点R的自由衰减振动响应的富氏变换在第r阶固有频率fr处的幅值;φrA与φrR分别为第r阶振型在测点A与参考点R的分量.
实际测量时往往采用数字功率谱分析,此时可以将自谱密度函数表示为
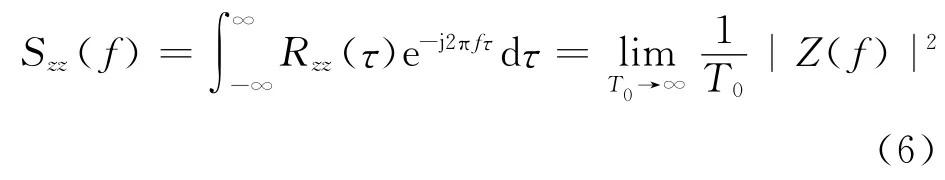
式中:T0为样本长度;Z(f)
由式(5)、式(6)与式(2),有
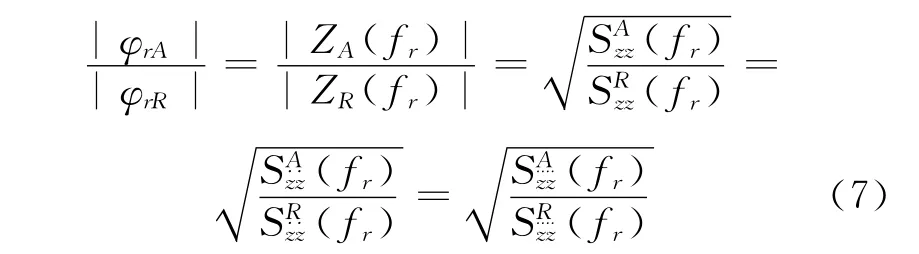
即可以采用各测点与参考点R的位移、速度或加速度自由衰减振动响应的自谱密度函数进行振型幅值的识别,振型相位的识别可以利用它们的互功率谱实部在此频率上的正负确定[6].
实际上,由文献[2]的式(5),振型相位的识别可近似由下式确定

式中:α为正的实常数;SAR(fr)为测点A与参考点R的自由衰减振动响应互功率谱在第r阶固有频率fr处的值.由于φrA与φrR均为实数,因此,互功率谱实部在频率fr处的正负确定了振型相位的正负.
需要指出的是,在振型测量时,往往使用多个传感器,这些传感器的灵敏度及其对应的放大器和滤波器的放大倍数都是不一样的,此时应该进行归一化的处理.
从式(2)可知,若采用加速度传感器得到的自谱密度函数在低频段的固有频率峰值比高频段的固有频率峰值小很多时,可以采用速度或位移传感器的自谱密度函数,也可以对加速度信号进行积分得到速度或位移信号,再进行谱分析.
2 激振方法的考虑
2.1 共振法(强迫振动法)
利用专门的激振装置,对结构施加激振力,使结构产生强迫振动,改变激振力的频率而使结构产生共振现象并借助共振现象来确定结构的动力特性.
2.2 脉动法(环境随机激振法)
利用外界各种因素所引起的结构微小且不规则的振动来确定结构动力特性.这种微振动通常称为“脉动”,它是由自然风、河流、地脉动、附近的机器或车辆等引起的扰动.
2.3 自振法(瞬态激振法)
自振法的特点是使桥梁产生有阻尼的自由衰减振动,记录到的振动图形是桥梁的衰减振动曲线.为使桥梁产生自由振动,一般常用突加荷载和突卸荷载2种方法.
共振法由于大型激振设备无法安装在桥面上,或者虽然有一些专用的激振设备,但现场试验条件及结构的复杂性等因素使这类专用激振设备的使用受到一定的限制,而且这种大型激振装置价格昂贵,将其用于桥梁动力特性试验会增加大量成本,因此,这种方法很少应用于桥梁动力特性测试.
脉动法比较适合于新建桥梁的测量,对于运营中的桥梁,特别是高速公路上的桥梁,长时间的道路封闭会产生较大的经济损失和引起交通不便,若不封闭交通进行的环境随机激振,由于车流量和车载大小在不同时段有很大差别,因此很难将激励谱看作是白噪声谱,否则将造成较大误差或识别困难.
环境随机激振法(脉动法)属于多输入多输出问题,而突加荷载法(冲击法)或称为自由衰减振动信号谱分析法则是单输入多输出问题.
目前,国内在桥梁结构模态测试中大多采用环境随机激振法[7-13],自由衰减振动信号谱分析法相对较少.然而,自由衰减振动信号谱分析法与环境随机激振法相比,有几个明显好处:(1)可以减少测量时间,对于长时间封闭道路引起交通不便和造成经济损失的情况,特别是对高速公路的桥梁荷载试验是非常有利的;(2)激励的能量大,可以有效提高信噪比,特别是在低频段;(3)跳车位置可以根据需要改变,以避开某些振型节点位置,对于特别需要关注的某些固有频率,可以在其模态位移最大的位置进行跳车,以便获得好的测试效果.
采用跳车自由衰减振动信号谱分析法需要注意的是对于中小桥粱,车辆自重的影响需要考虑.
3 传感器布置的考虑
从理论上来说,如果传感器没有放置在某阶振型的节点处,则一个传感器的测量信号频谱图就可以得到结构的各阶固有频率,然而,由于激励并非是完全的白噪声激励,加上其他干扰信号的影响,因而测量信号频谱图上除了在结构固有频率处出现共振峰外,在其他一些频率处也常常会出现峰值,此时,要确定结构的固有频率就显得比较困难,而传感器的合理布置可以较好的解决这个问题.
对于桥梁结构,通常比较关心前几阶固有频率,此时可以根据计算得到的桥梁结构前几阶振型来布置传感器.
图1给出了一般中承式钢管混凝土拱桥的前2阶竖向弯曲振型,若要测量这两阶频率,可以在拱肋(或桥面)的L/4和L/2处各布置1个竖向传感器,可以看到,L/2位置是桥梁第一阶振型的节点,其响应信号对第一阶固有频率而言能量很小,因此可以预期其频谱图上在第一阶固有频率处不会出现峰值或峰值很小,而L/4处则会出现明显峰值,由此可以容易分辨出结构固有频率.

图1 某特大桥结构竖向弯曲振型图
图2 给出了2座钢管混凝土拱桥(净跨分别为123m中承式钢管混凝土提篮拱桥和190m中承式钢管混凝土桁架拱桥)桥面L/4位置跳车时桥面各测点竖向加速度响应谱.从图2a)可见,测点L/2在第一阶固有频率处没有出现峰值,仅在第二阶固有频率处出现峰值,而测点L/4则在第一阶和第二阶固有频率处都出现了峰值.同样从图2b)中可见,测点L/2在第一阶固有频率处没有出现明显峰值,而测点L/8,L/4和3L/8则在第一阶和第二阶固有频率处都出现了峰值,这表明测量结果与振型图的分析是一致的,而且固有频率测试值与计算值吻合良好.
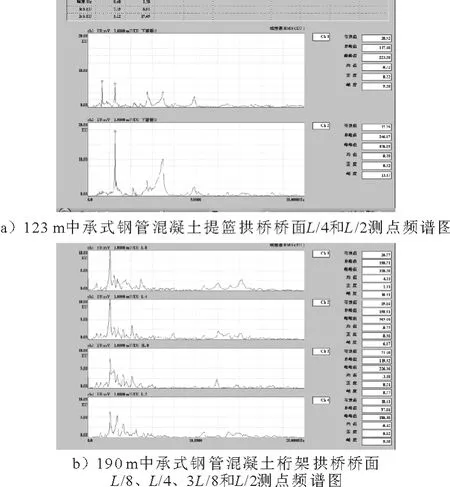
图2 2座钢管混凝土拱桥桥面L/4位置跳车时各测点竖向加速度响应谱图
4 结 论
1)自由衰减振动信号谱分析法与环境随机激振法从本质上来说是同一方法,它们的激励信号自谱密度函数在较宽的频带内均为一常数.
2)环境随机激振法,比较适合没有通车的新建桥梁的动态特性参数测试或桥梁结构长期健康监测,而自由衰减振动信号谱分析法则非常适合桥梁封闭时间不能太长特别是已通车的高速公路桥梁荷载试验中动态特性参数的测试.
3)传感器布置测点不一定全部布在振型幅值最大处,个别测点布置在振型节点处,常常更容易识别各阶固有频率.
4)钢管混凝土拱桥的跳车激励位置应选择在前几阶振型幅值都较大的部位(如L/4处),而L/2处是钢管混凝土拱桥的第一阶振型节点位置,在此处激振会使信号功率谱不出现第一阶共振峰.
5)跳车激励时要注意车辆自重对固有频率的影响分析,对于车辆质量相对于桥梁质量很小的,车辆自重影响可以忽略不计,对于中小桥梁情况,车辆质量的影响不能忽略,需要进行质量影响的固有频率修正.
[1]陈宝春.钢管混凝土拱桥设计与施工[M].北京:人民交通出版社,1999.
[2]于德介,陈敏均,朱之基.斜拉桥桥面振动测试与分析[J].中南公路工程,1991,59(4):43-47.
[3]徐日昶.桥梁检验[M].北京:人民交通出版社,1989.
[4][英]纽兰D E.随机振动与谱分析概论[M].方 同,译.北京:机械工业出版社,1980.
[5]邹经湘,结构动力学[M].哈尔滨:哈尔滨工业大学出版社,1996.
[6]陈常松,田仲初,郑万泔,等.大跨度混凝土斜拉桥模态试验技术研究[J].土木工程学报,2005,38(10):72-75.
[7]宋 雨,刘红国,张 军.斜拉桥模态测试与分析[J].中国市政工程,2004(1):33-34.
[8]胡利平,韩大建,禹智涛.基于环境激励的大跨度桥梁模态试验[J].广东工业大学学报,2005,2(1):100-104.
[9]任伟新,林友勤,彭雪林.大跨度斜拉桥环境振动试验与分析[J].实验力学,2006,21(4):418-426.
[10]孙正华,李兆霞,陈鸿天,等.大跨斜拉桥基于结构模拟的环境振动测点优化布置[J].应用科学学报,2007,25(4):411-417.
[11]章关永,刘进明.上海卢浦大桥主桥动力特性测试研究[J].振动与冲击,2008,27(9):167-170.
[12]刘荣桂,周士金,许 飞,等.CFRP拉索斜拉桥模态试验与分析[J].桥梁建设,2009(3):29-32.
[13]王荣辉,蔡禄荣,黄永辉,等.双层公路特大桥的模态参数识别及成桥模型分析[J].华南理工大学学报:自然科学版,2011,39(6):113-118.
