一种自适应的循环不变式生成方法

刘自恒，曾庆凯,b

(南京大学 a.计算机科学与技术系；b.计算机软件新技术国家重点实验室，南京 210093)

1 概述

软件的任何漏洞都可能导致非常严重的后果。无论是软件设计人员还是软件的用户，均希望在软件系统投入在正式使用之前，能得到软件正确性的保证。通过测试可以在一定程度上保证软件的正确性，但成本较高，不能完全保证软件的可靠，而且测试只能发现程序中的错误，不能证明程序无错。从另一个角度考虑，如果可以从理论上证明程序符合预期的行为或者没有某种错误，同样可以认为软件是可靠的。20世纪50年代出现的形式化方法思想，以严格的数学和逻辑理论为基础，适合于软件和硬件系统的描述、开发和验证。

1967年，Floyd提出采用形式化方法证明程序的正确性，经过多年的研究，取得了一系列理论和实践的重大进展。在形式化分析验证程序时，以Floyd-Hoare逻辑为基础，将程序转换为抽象模型，进行逻辑归纳演绎，验证程序是否满足程序规范。使用形式化的思想对程序进行分析验证并不排斥测试，但可以认为它是一种更好的测试框架。在分析验证时开发者给出要验证函数的规范，但是在低层次结构上(如基本指令、分支、循环结构等)需要验证程序自动地推导这些结构的规范，表达出它们实现的语义。对于基本的结构，如赋值和分支，Hoare逻辑已经给出了直接的转换规则；但是循环结构中需要循环不变式来证明循环初始时和执行过程中均保持的性质，而 Hoare逻辑没有给出直接的生成循环不变式的规则，这是因为并不存在通用的不变式生成规则。因此，形式化程序分析的一个关键性难点在于程序中循环结构的存在，而且实际的循环结构中常常又有嵌套循环和分支结构，操作的数据类型除矢量型变量外，还包含数组等向量型变量，使得循环不变式的生成工作变得困难。

本文分析、总结了当前常见的循环不变式生成方法，并提出一种改进的循环不变式生成方法，并通过实验评价其分析性能。

2 现有方法

通常对于给定的函数前置条件和后置条件，不变式并不是唯一的，开发人员往往增量地得到不变式：首先预测不变式，然后通过观察程序行为来逐步细化预测的不变式[1]，最终得到验证所需要的不变式信息。计算循环不变式的方法主要有下面的几种。

2.1 基于迭代不动点的计算

使用该方法的技术有数据流分析、模型检测和抽象解释等。在计算程序的状态转换过程中，连续地计算直到得到数据流方程的最小不动点，当发现程序状态不再变化时，认为发现不动点。计算的过程是一个不断迭代直到收敛的过程。但计算过程的收敛性是不可判定的，因此需要一些技术来保证和加速收敛的过程，如使用放大算子、提高抽象粒度等。

使用放大算子会导致一定程序的精度损失，因此，要尽可能地延迟使用放大算子的时机，如使用前向放大[2]，同时在合适的位置再使用缩小算子。其他的加速措施也存在同样的问题，需要在效率和精度之间取一个合理的平衡点。

2.2 基于参数化模板

该方法主要针对线性数值计算程序进行。计算时通过程序或开发者指定目标不变式的模板形式，其中变量的系数未知，称为模板参数；程序经过抽象解释映射为抽象域上的转换系统；使用不同的技术求解模板中的系数，得到不变式。根据与结合求解的技术不同，又可细分如下：

(1)与约束求解结合。首先由开发者或程序默认为循环指定一个带参数的不变式模板，其中变量的系数未知；随后采用归纳断言方法，建立不变式之间以及不变式与循环的前置条件之间的约束，再利用 Farkas定理[3]，消除约束中出现的程序变量，并表达出循环相关的条件，得到关于模板参数的非线性约束，从而将线性循环不变式构造问题转化为约束求解问题。最后，使用因式分解、线性规划或非线性求解器等方法求参数的数值解。基于约束的方法相对于基于不动点计算的方法有如下优点：目标指向性明确，效率更高。不需要使用难以控制的放大方法，精确损失小[4]。

(2)与可满足性(Satisfiability,SAT)求解结合。先将约束化为合取范式，然后利用Farkas定理消除约束中的程序变量，再将约束中的参数建模为比特向量(bit-vector)，进而将该约束转化为布尔公式，使用SAT求解器搜索满足约束的参数值。该方法受益于SAT求解技术的进步。

(3)与量词消去结合[5-6]。如果通过循环完成对数组的操作，则不变式公式中将含有量词，无法直接使用约束求解或SAT求解，需要先将其中的量词消去得到与之等价的不包含量词的公式，然后再使用约束求解或SAT求解的方法来解。

面向验证性质的增量式归纳不变式构造方法[7]。该方法根据验证不成立时，求解器返回的虚假反例增量式地生成归纳的不变式，这样提高了生成不变式的效率，能够得到刚好满足验证需求的不变式性质。

在基于参数化模板的不变式生成方法中，增加模板大小可以有更大机会使得前置条件适应模板，但会生成更大的 SAT式子要求解[4]，使得求解所需的时间和空间变大。对于模板形式的选择，文献[4,8-9]由用户指定不变式模板(同时程序提供了默认的模板可以使用)，文献[4]既可以由用户指定模板(如指定未知关系式析取范式表示中合取和析取数量的最大值)，也提供了一种迭代增加模板大小的方案，直到发现某个解。适用范围方面，文献[10]只处理简单while程序并针对线性算术运算，文献[11-12]只能处理一个简化了的程序语言，等同于一个C语言的子集，文献[13]扩大了文献[11]的适应范围。

这种生成不变式方法并不是归纳的，求解之前需要开发者给出正确的模板形式；应用扩展性受限于约束求解器的求解能力；对于这种生成方式，用户指定的模板形式固定，需要与用户交互，对使用者来讲比较繁琐，适应性不强。

2.3 基于机器学习和实际执行的方法

文献[1,14]提出可以通过机器学习的方法来推断循环不变式。而Daikon[15]是动态不变式发现器，可以探测包括C、C++、Java、Perl语言编写的程序和含有记录型结构的数据类型。

3 改进方法

通过前面的介绍可以发现，现有的不变式生成方法存在以下不足：(1)处理程序能力往往有限，通常假定处理某个简单的程序语言，应对复杂的C语言能力不足。(2)使用了参数化模板求解的方法，其灵活性不足，需要开发者在对程序深刻理解的基础上指定模板形式，然后对模板系数求解，不能自动地考虑程序中的操作语义信息。(3)现有的方法有的只关注循环内容本身，有的除循环外只关注了循环外的某一点信息，没有综合考虑函数规范、循环本身、循环后操作等内容，使得生成的不变式不够全面。(4)现有的工作没有从执行不变式生成分析，其分析结果是否使得函数规范得以顺利完成验证方面进行检验，而这正是进行不变式生成分析的原始出发点，现有工作缺乏一定的实践性评估。

本文提出以下改进思路，基于条件赋值转换和自适应模板规则生成循环不变式，在生成过程中综合考虑函数规范、循环本身、循环后操作等信息，这样能更有针对性地、自动地发现潜在的循环不变式，但这种分析是一种保守的分析，会产生并不正确的不变式，需要进行验证；对分析的结果，除了评价不变式本身的正确性外，还从程序验证的角度，根据分析结果是否使得验证顺利完成，对其有效性进行分析。

3.1 条件赋值转换

基于条件赋值转换控制流的思想，这里提出一种条件赋值转换的方法。对于循环中的每一条赋值语句，直接根据分支条件和赋值操作类型的不同，转换得到不同的候选不变式，转换的规则主要有下面的几种，本文参考文献[16]的一些做法，执行一些变量变换。这里假定循环开始时变量x的取值范围为集合x0，它可以是离散的集合，也可能是连续的区间；P表示更新操作的内容，包含四则运算、指针引用等。标量变量指只包含一个值的变量，如C语言中的基本数据类型，矢量变量指包含一系列值的变量，如数组。这里不考虑包含用户自定义数据类型的赋值操作。

(1)分支判断条件和赋值操作都是标量型变量操作(非数组、指针变量)：

(2)分支判断条件为标量型变量，赋值操作为数组访问操作，若数组A长度为len：

(3)分支判断条件是关于下标的判断，赋值操作为数组访问操作，若数组A长度为len：

(4)分支判断条件是关于数组元素值的，赋值操作为数组访问操作，若数组A长度为len：

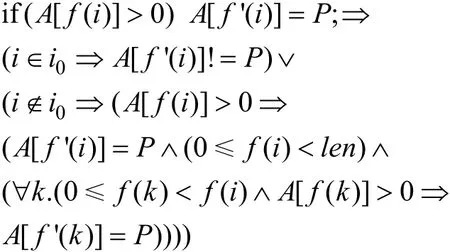
(5)分支判断条件是关于同一数组元素之间值的，赋值操作为数组访问操作，若数组A长度为len：

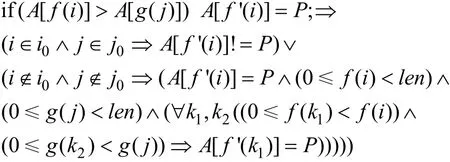
(6)分支判断条件是关于2个数组元素之间值的，赋值操作为数组访问操作，若数组A长度为len1，数组B长度为len2：

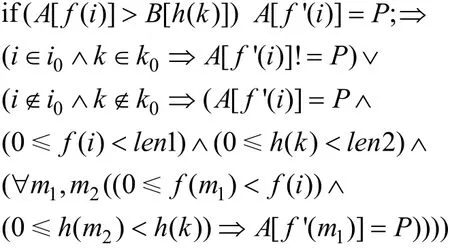
在上面的转换规则中，如果数组的长度不能确定，则排除对于下标表达式上界的约束表达。

正确性说明。以第(1)条规则为例，其他的与之类似。结果由两部分构成。当变量x∈x0时即变量在初始值范围内时，由于未执行赋值操作，具有属性y!=P；当变量值不在初始值范围内时，认为是在循环中，当满足路径条件f(x) ＞0时，执行赋值操作，因而有 f(x) ＞0⇒ y=P。这些转换规则是对于程序语义的直观的逻辑转换，同时通过变量转换等方式表达了有关数组下标变换的属性；但由于忽略了变量间的别名关系、变量的值范围分析并不总是准确等元素，导致转换结果存在过近似的问题，因此需要验证其正确性。

3.2 自适应模板生成

这里的模板生成不变式的方法和前面的有所不同，不是根据指定的模板形式求解未知的模板变量系数，而是以一种启发式的方法生成模板形式表达的候选不变式。本文希望从程序的语义信息出发，结合程序变量的取值情况，使用模板形式表达出变量之间存在的约束关系。而模板变量的系数则从程序中提取得到。这样可以自动地寻找程序中最有可能存在的不变式约束关系，适应具体程序的语义特点，不需要用户来指定模板的形式。但这种表达可能不是精确的，也可能是错误的，因而需要验证其真假，验证的过程可以由定理证明器完成，也可以在计算不动点时根据程序的状态在抽象域上求解模板约束关系是否可满足。

这些启发式生成的循环不变式是根据从程序中提取到的信息按照生成规则得到的，这些信息包括要验证的程序规范、程序中的属性断言、程序变量操作的方式、程序变量可能的系数、程序变量的取值范围等。因此，如果可以进行更加细节的操作分类，提出更多的模板生成规则，则可以发现更多的不变式。

目前定义的生成规则主要从以下方面考虑：

(1)根据预定义谓词生成，判断某组变量是否可以使得该谓词属性成立，判断由定理证明器判断，这些谓词一般是比较简单的属性，如判断某个变量取值是否单调变化、数组中的元素是否相等；这里判断的变量类型必须是和谓词中的变量类型相兼容的。

(2)被调用函数是否有函数规范，如果有将相应的参数变量应用于规范中的谓词中，则得到被调用函数的操作结果。如果没有函数规范，则忽略函数调用。被调用函数的函数规范是其后置条件，表达了调用它对变量产生的“影响”，是函数具体内容的一种摘要表示。因此，这里的分析是一种使用了函数摘要的半过程间的分析。

(3)收集程序中的常量信息，主要是函数规范中、循环后断言和条件判断中的常量。

(4)根据从循环体内、循环后的 assert语句和其他分支判断条件收集到的变量和变量的系数信息，生成变量间可能的模板约束关系。如果分析关注的变量集Var，个数为N；对于长度T的模板，即从Var中选择T个变量组成模板。但有的抽象域限制系数值和变量数量，如八边形域中限制变量系数只能为1、0或者−1，限制模板变量数量为2。

当生成模板时，从Var中选择指定数量的变量作为模板变量，枚举选定的模板变量的所有系数组合，对于系数不为0的变量，累加其最大值(最小值)的和。生成的模板具有如下形式：

其中，op ∈{＞,≥,==,!=},ci∈ coefv,c∈Const∪{m in,m ax}，cofv是变量v的候选系数集合，Const是收集到的常数值集合，min、max分别是选定的系数不为0的模板变量的最小值、最大值。

3.3 优化措施

从分析处理的范围和方法可知，分析验证的复杂度不仅与程序规模有关，更与要分析的变量个数、模板中变量的个数、每个模板变量候选的系数个数有关。在模板大小一定时，当程序规模较大、要分析的变量增多时，需要验证的情况急剧增加；而增大模板尺寸时，需要验证的情况也会急剧增加。如果有N个变量，每个Vair变量有ni个候选的系数，提取到C个常数，由之前的模板生成规则，如果模板里面最多可以含有T个变量(即模板尺寸为T)，则最多需要枚举验证种情况，可以看出其具有较高的复杂度，因此为了使分析过程及时有效地终止，需要执行一些剪枝优化策略，以压缩要分析验证的不变式数量，本文采用的策略如下：

(1)控制关注的变量数量。分析时不分析过程中所有的变量，只分析当前循环中使用的变量、循环后条件中的变量，除此之外的变量与当前循环的关联性较弱。忽略不能处理的数据类型(如结构体)变量。当有循环嵌套时，该策略避免了大量的重复分析。从其复杂度公式可以看出，减小分析的变量数量可以缩减模板数量。

(2)限制模板尺寸T。当T增大时(T＜N /2)，C随之增大。验证者可以指定模板的尺寸，例如这里默认设定为3，即模板中最多含有 3个变量。从其复杂度公式可以看出，减小模板尺寸可以缩减模板数量。

(3)屏蔽指针本身的分析，只关注指针指向变量的值即指针引用。忽略非标准数据类型，如结构体、枚举等类型变量。将数组元素和一般标量变量的操作区分开来，不放在同一个模板中。这样可以减少候选的不变式模板个数。

(4)使用改进的搜索策略。基本的思想是：如果I＞0成立，则I ≥0一定成立，不需要再验证，而且它是冗余的，只需要返回I＞0即可；如果I＞0成立，则I≤0一定不成立，它们是互斥的。判断过程如下。

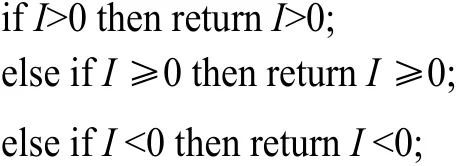
(5)在生成模板时，首先执行依赖分析，判断变量之间是否有依赖关系(包括数据依赖和控制依赖)，不存在依赖关系时认为它们之间联系较弱，不应该一同构成循环不变式。

4 实现与实验结果

4.1 loopInv设计与实现

本文基于Frama-C平台和APRON库对上述方法做了实现，作为一个插件 loopInv集成在 Frama-C中。其在Frama-C的位置和处理流程如图1所示，其内部结构如图2所示。

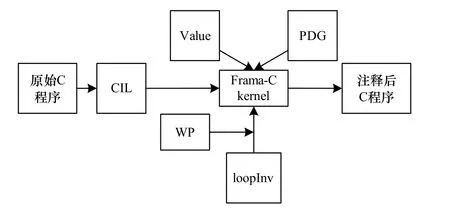
图1 loopInv分析框架

图2 loopInv框架设计

预处理阶段完成的工作有：收集要验证的函数规范、数组变量信息、循环中的分支条件和其后的断言条件集合、程序中的常量信息、模板变量的候选系数集合、循环中赋值语句的路径约束条件等信息。在生成转换系统时，循环中加入模板约束表达式。验证时使用 WP插件和 APRON库可满足性求解。

4.2 实验结果

实验中选取了2组程序进行分析，评估loopInv的有效性。一组是简单的示例程序，对于这类程序同时用其他不变式生成工具进行分析，或分析符合工具特定要求的与之等价的程序，和loopInv对比实验结果，这里使用的对比工具是invGen[8]和gin-pink[16]；这些程序来自其他文献，或出自 WP的测试程序，先将手工书写的循环不变式去除；另一部分是规模较大的实际的开源C程序，由于对比工具或者还不能处理这样规模的程序，或者进行等价转换工作量较大，不再进行对比分析，这里侧重关注发现的不变式数量，不再验证函数规范。

选用的测试对象如表1、表2所示。这里变量个数是指作为模板变量的变量数量。

表1 测试程序1

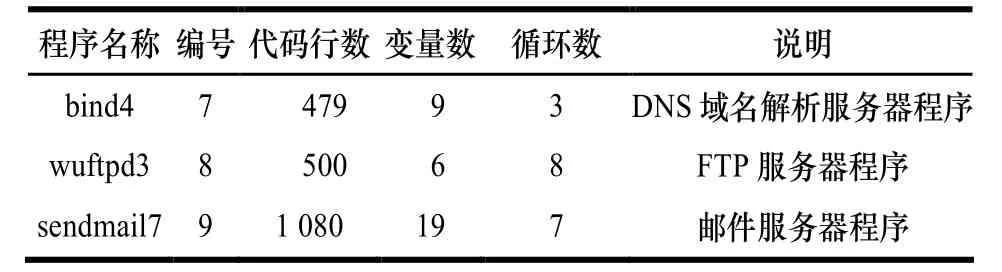
表2 测试程序2

分别设定模板尺寸为 2和 3，得到的实验结果分别如表3和表4所示。其中，列C1～C8分别表示程序编号、输出不变式个数、实际正确不变式个数、错误不变式个数、经分析后程序是否得到证明、分析执行时间(s)、总的执行时间(即包含验证不变式时间，时:分:秒)、峰值内存(MB)。

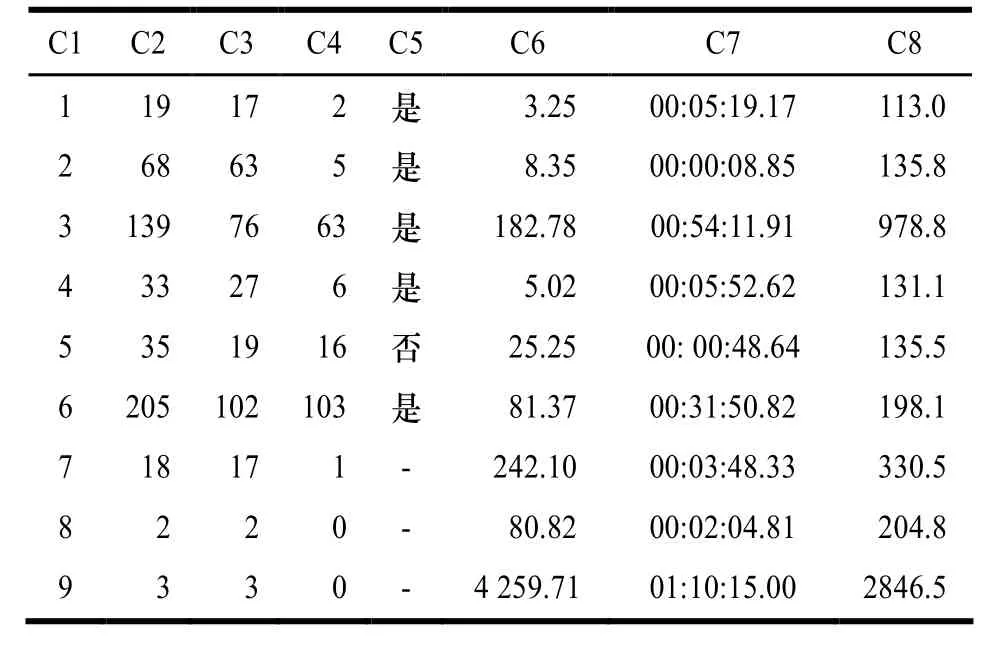
表3 loopInv实验结果统计1

表4 loopInv实验结果统计2

同时，选择工具invGen和gin-pink对程序1～程序6进行不变式分析，得到的结果如表 5所示。其中，列Ca～Ce分别表示程序编号、输出不变式个数、程序是否得证、总的执行时间(分:秒)、峰值内存(MB)；各个统计项的第 1列是 invGen的分析结果，第 2列是 gin-pink的分析结果，gin-pink输出不变式个数一列中，括号外表示候选的不变式个数，括号内表示正确的不变式个数。

表5 其他工具分析结果统计

从实验结果可以看出，通过分析，多数函数规范得到了验证，说明分析过程是有效的；模板尺寸的变大时生成的不变式数量急剧增多，这能够发现更多的循环不变式，但同时求解所需要的时间和空间都发生了增长，特别是求解时间增长很快；而实验结果也表明，设定较小的模板尺寸时，得到的不变式分析结果也可以满足多数验证的需求；求解需要的时间和空间不仅与程序规模陒关，更加与程序本身的操作方式陒关。当程序变量数量较多、操作变化灵活、程序结构变化复杂、变量中含有数组等类型时，需要分析的情况增多，分析的难度也随之上升；陒比invGen和gin-pink，loopInv具有更好的适应性和有效性。

5 结束语

针对当前自动生成循环不变式方法存在的一些局限性，本文综合考虑函数规范、循环本身、循环后操作等信息，提出一种基于条件赋值转换和自适应模板生成技术的生成方法，并设计实现了一个Frama-C的插件loopInv。实验结果表明，该方法具有良好的适应性，能够使得实验中的大部分程序验证过程顺利完成。今后需要在细化分析程序操作的基础上，进一步完善不变式生成规则，同时优化分析过程，以适应更大规模的程序。

[1]Jung Y,Kong S,Wang B,et al.Deriving Invariants by Algorithmic Learning,Decision Procedures,and Predicate Abstraction[C]//Proc.of the 11th International Conference on Verification,Model Checking,and Abstract Interpretation.Madrid,Spain: Springer,2010.

[2]Gopan D,Reps T W.Lookahead Widening[C]//Proc.of the 18th International Conference on Computer Aided Verification.Seattle,USA: Springer,2006.

[3]Bradley A R,Manna Z,Sipma H B.Linear Ranking with Reachability[C]//Proc.of the 17th International Conference on Computer Aided Verification.Edinburgh,UK: Springer,2005.

[4]Gulwani S,Srivastava S,Venkatesan R.Program Analysis as Constraint Solving[C]//Proc.of ACM SIGPLAN Conference on Programming Language Design and Implementation.Tucson,USA: ACM Press,2008.

[5]Kapur D.Automatically Generating Loop Invariants Using Quantifier Elimination[J].Deduction and Applications,2006,64(1): 54-75.

[6]Monniaux D.A Quantifier Elimination Algorithm for Linear Real Arithmetic[C]//Proc.of the 15th International Conference on Logic for Programming,Artificial Intelligence,and Reasoning.Doha,Qatar: Springer,2008.

[7]Bradley A R,Manna Z.Property-directed Incremental Invariant Generation[J].Formal Aspects of Computing,2008,20(4):379-405.

[8]Gupta A,Rybalchenko A.InvGen: An Efficient Invariant Generator[C]//Proc.of the 21th International Conference on Computer Aided Verification.Grenoble,France: Springer,2009.

[9]Hart T E,Ku K,Gurfinkel A,et al.Ptyasm: Software Model Checking with Proof Templates[C]//Proc.of the 23th IEEE/ACM International Conference on Automated Software Engineering.L'Aquila,Italy: IEEE Press,2008.

[10]Podelski A,Rybalchenko A.A Complete Method for the Synthesis of Linear Ranking Functions[C]//Proc.of the 5th International Conference on Verification,Model Checking,and Abstract Interpretation.Venice,Italy: Springer,2004.

[11]Lalire G,Argoud M,Jeannet B.Interproc[EB/OL].(2008-10-21).http://pop-art.inrialpes.fr/people/bjeannet/bjeannet-forge/interproc/index.html.

[12]Moy Y,Marché C.Modular Inference of Subprogram Contracts for Safety Checking[J].Journal of Symbolic Computation,2010,45(11): 1184-1211.

[13]邢建英,李梦君,李舟军.CILinear: 一个陑性不变式自动构造工具[J].计算机科学,2010,37(12): 91-95.

[14]Jung Y,Kong S,David C,et al.Automatically Inferring Loop Invariants via Algorithmic Learning[C]//Proc.of MSCS’12.[S.1.]: IEEE Press,2012.

[15]Ernst M D,Perkins J H,Guo P J,et al.The Daikon System for Dynamic Detection of Likely Invariants[J].Science of Computer Programming,2007,69(1-3): 35-45.

[16]Furia C A,Meyer B.Inferring Loop Invariants Using Postconditions[M].Berlin,Germany: Springer [s.n.],2010.

[17]Sharma R,Dillig I,Dillig T,et al.Simplifying Loop Invariant Generation Using Splitter Predicates[C]//Proc.of the 23th International Conference on Computer Aided Verification.Cliff Lodge,USA: Springer,2011.

[18]Kovács L,Voronkov A.Finding Loop Invariants for Programs over Arrays Using a Theorem Prover[C]//Proc.of the 12th International Conference on Fundamental Approaches to Software Engineering.York,UK: Springer,2009.