兼容弱连通簇的Ad Hoc网络分簇算法

肖 磊，符云清，钟明洋，王兴芹

(重庆大学 a.计算机学院；b.软件学院，重庆 400044)

1 概述

Ad Hoc网络(MANET)是由一组可同时充当普通终端和路由器的无线节点构成的多跳、自组织的移动网络。Ad Hoc网络具有部署简单、成本低、自愈能力强等特点，在军事、抢险救灾和民用等领域都有广泛的应用[1]。由于网络中节点可任意移动，没有固定拓扑和主干，路由策略设计便成为MANET的核心问题。目前，研究者提出了很多适合MANET的路由协议，如目的节点序列距离矢量(Destinationsequenced Distance-vector Routing,DSDV)协议、动态源路由(Dynamic Source Routing,DSR)协议、按需距离矢量(Ad Hoc On-demand Distance Vector Routing,AODV)协议等。但这类算法开销不容忽视，尤其不适应节点规模大、拓扑结构变化快的Ad Hoc网络。

Ad Hoc网络分簇是一种降低路由开销的有效方法。分簇将集中控制的思想运用于分布式管理中，把网络的重构限制在局部范围内[2]，能有效减少局部拓扑变化引起全局变化现象的发生，从而降低网络的整体路由开销。在分簇的MANET中，每个簇由一个簇首和多个簇成员组成。簇首负责维护簇内拓扑结构，并为簇间通信提供支持。

根据簇结构的大小，分簇算法可分为单跳簇结构分簇算法和多跳簇结构分簇算法。其中，国内外比较受认可的单跳分簇算法主要有以下3类，即基于最小ID的分簇算法(Minimum ID Clustering Algorithm,MIDCA)、基于最大节点度的分簇算法(Highest Degree Clustering Algorithm,HDCA)、多因素加权的分簇算法(Weighted Clustering Algorithm,WCA)。

基于最小ID的分簇算法MIDCA根据节点的ID来生成簇[3]。节点与邻居的ID进行比较(已是簇成员的邻居节点不参与比较)。若自己 ID最小，则成为簇首并广播消息；若其ID不是最小，则等待，直到收到簇首广播消息，此时节点可加入该簇。该算法实现简单、收敛快，但网络中ID较小的节点倾向当选簇首，容易因能量消耗过快而死亡，具有很大的不公平性。基于最大节点度的分簇算法依据节点的度来成簇[4]。其算法过程与基于最小ID的分簇算法类似，不同的是节点在获取邻居矩阵后需计算自己的度，即邻居的个数，并选择度最大的节点作为簇首。该算法收敛较快，但该算法倾向于度较大的节点为簇头，簇内节点过多将导致簇内节点吞吐量降低。多因素加权的分簇算法主要的思想是对节点的多种网络参数(如带宽、剩余能量、节点度、移动性等)进行加权求和，权值最大的节点为簇首[5-6]。该算法考虑因素全面、簇首选择更优，但多种网络参数的变化，造成其权值变化较快、收敛相对较慢，因此，网络情况的变化对算法性能影响极大。

单跳簇结构覆盖范围小，簇内节点活动范围相对较小、易脱离簇首，为优化整个网络的簇划分，提高簇结构稳定性，近年来多跳分簇算法也引起了广泛研究。多跳分簇算法为单跳分簇算法的扩展，即簇首在节点多跳范围内进行选择。文献[7]提出一种基于主宰树的分簇算法(Dominating Tree Based Clustering Algorithm,DTCA)，利用节点在两跳范围的度(即两跳范围内的邻居个数)选择出主宰节点构成网络虚拟骨干网，并根据平均邻居(是关于节点两跳邻居个数的函数)将主宰节点进行划分，得到簇的骨干树结构，其余非主宰节点为骨干树的叶子节点，即普通簇成员。树根为簇首，其他主宰节点则为备选簇首节点。该算法分布式执行的，无法保证主宰节点构成的虚拟骨干网覆盖整个网络，即无法使所有非主宰节点到该虚拟骨干网的距离为一跳。文献[8]根据节点的度和节点的剩余能量构成的综合指标来构成主宰集，并最终生成多跳的簇结构，该算法能保证主宰集的连通性，但簇结构维护开销较大。

目前，主流的多跳分簇算法是在单跳分簇算法的基础上进行扩展，选择主宰节点构成网络的虚拟主干网[9]，并最终生成多跳簇。利用主宰集可保证簇结构的连通性，即形成强连通簇。由于算法分布式执行，这类旨在构造强连通簇的分簇算法不能保证选择最优的节点作为簇首。为解决这一问题，并提高簇结构稳定性，本文提出一种兼容弱连通簇的分簇算法(Clustering Algorithm Compatible with Weak Connection Cluster,CACWC)。

2 兼容弱连通簇的分簇算法

单跳簇结构簇覆盖范围较小，簇成员更容易移动出簇，不利于将网络的重构限制在局部，并且分簇数过多，簇间通信延迟较大，而多跳簇结构簇覆盖多跳节点，虽能减少分簇数，但覆盖的跳数越大，簇结构维护开销就越大，簇首资源消耗也更快，因此，着重研究两跳范围的分簇算法。在不构建主宰集的前提下，生成两跳簇结构，任一簇成员到达簇首的最大距离为两跳，簇内节点间的最大距离为4跳。但是，CACWC并不是使得最终的簇结构均是弱连通簇，而是弱连通簇与强连通簇并存。

2.1 相关定义

定义 1(强连通簇) 在一个簇结构中，簇内节点集合为S，若任一节点v∈S可到达簇首节点，则该簇为强连通簇。

定义 2(弱连通簇) 在一个簇结构中，簇内节点集合为S，若存在一节点v∈S必须通过簇外节点才可到达簇首，则该簇为弱连通簇。

图1为两跳强连通簇，图2为两跳弱连通簇，其中，节点13需通过簇外节点8才能到达簇首节点7。对于两跳弱连通簇而言，簇内成员节点至多通过一个簇外节点到达簇首。

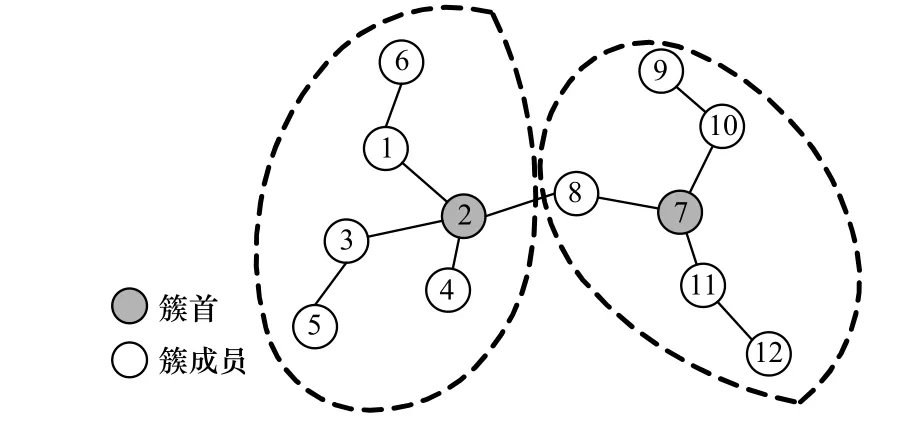
图1 两跳强连通簇

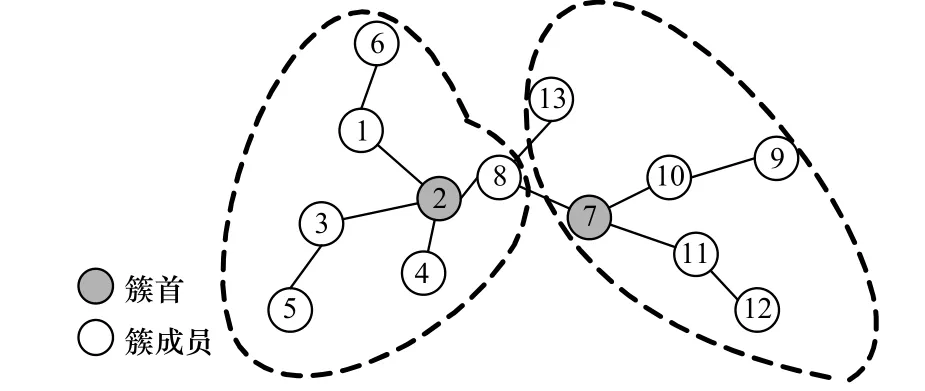
图2 两跳弱连通簇

分簇算法弱连通簇存在的必要性分析如下：在多跳簇中，弱连通簇与强连通簇相比，簇成员可通过簇外节点到达本簇簇首，能够选择更优的节点作为簇首，如图 2的两跳簇中，节点两跳范围内有2个簇首节点2、节点7，由于分簇算法分布式执行的原因，现除节点13外，其他节点都已加入簇。设对于节点13来说，节点7比节点2更适合作其簇首(根据剩余能量、带宽等因素判断)，此时，若必须满足强连通条件而选择节点2作为簇首，则将加重节点2的负担，甚至导致节点 2的能量快速耗尽。若以弱连通的选择标准，则可选择节点7作为簇首，节点13通过另一簇的簇内成员节点8与簇首通信。这样簇首节点2、节点7的负载相对更均衡，有利于簇结构的稳定。

定义3(最佳簇大小) 簇内成员的最佳个数。

当网络规模一定时，簇成员最佳个数一般为常值，根据文献[10]，其计算公式为：

其中，W1、W2表示簇内、簇间的通信带宽；N为网络节点个数。通过最佳簇大小可限制簇内成员个数，防止簇内节点过多而导致簇头负载过大[11]。

定义 4(簇首候选标准) 自由状态下节点本身的簇首衡量指标。计算公式如下：

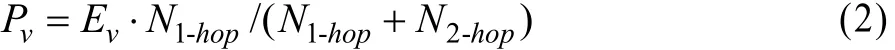
本文自由状态下的节点即是指未加入簇结构的节点。其中，Ev表示节点v的剩余能量；N1-hop表示距离节点v的一跳的节点个数；N2-hop表示距离节点v的两跳节点个数。节点剩余的能量越高，一跳邻居数占节点v两跳范围内邻居总数的比例越大，其当选簇首的可能性越大。能量越高表明，其当选簇首的时间将更长，N1-hop/(N1-hop+N2-hop)越大，则当选簇首后，簇内节点到达簇首路径将多样化，簇结构将更健壮。

定义 5(簇头潜力规则) 在簇首候选标准的基础上，簇头潜力规则考虑了节点簇状态、簇结构制约因素，具体如下：

(1)簇成员节点簇首潜力为 0，即簇成员节点在未脱离簇之前不会成为簇首。

(2)对于已是簇首的节点而言，若簇内成员个数超出上限C△，则簇首潜力为0，即节点不会加入满员的簇。

(3)Pv越大节点簇头潜力越大。

(4)未加入簇的节点其簇内成员节点默认为0。

(5)若 Pv相等，且簇内成员个数未超出上限 C△，簇内节点个数越小的节点簇头潜力越大。

2.2 邻居表的设计

本文的邻居表为十字链表结构的两跳邻居表，其逻辑结构如图 3所示，纵向为双向链表，表示节点两跳内的邻居；横向为节点到达相应的邻居节点的中间节点。一跳邻居的横向链表为空。邻居表的结构如图4所示。

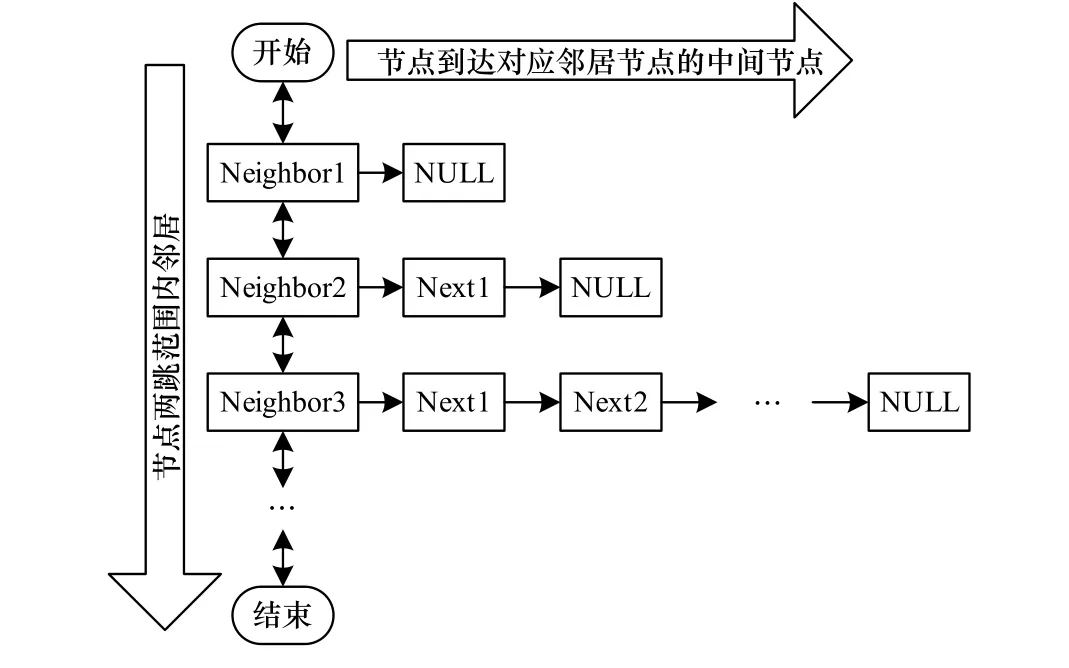
图3 两跳内的邻居表逻辑结构

图4 邻居表节点结构

邻居表节点各个字段意义如下：

(1)节点标识符(NID)：节点的唯一标识符。

(2)簇状态(CS)：节点当前的簇状态，若为簇首则为1，若为簇成员则为0，若未加入簇则为−1，刚加入网络的节点其初始状态为−1。

(3)所属簇标识符(CID)：节点所属的簇ID，簇标识符由簇首节点的NID决定，若节点未加入簇，则该字段置空。

(4)所属簇簇成员数(N)：簇内成员个数，CS为−1的节点簇成员个数默认为0。

(5)簇首候选标准：标识节点本身可当选簇首的衡量指标，由式(2)算出。

(6)中间节点集：到达该邻居节点的所有中间节点，若该邻居节点为一跳邻居，则该字段为空；若为两跳邻居，则为到达该邻居的所有中间节点的NID。

(7)中间节点：当前用于与该邻居节点通信的中间节点，若该邻居节点为一跳邻居，则该字段为空；若为两跳邻居，则为到达该邻居的中间节点的NID，来源于中间节点集。

邻居表的构造规则如下：节点邻居表结构由Hello机制更新，Hello响应消息包括节点自身信息及其一跳邻居的信息。在构造邻居表时，若是一跳邻居则纵向链表头部开始插入，具体插入位置以邻居节点簇头潜力排列，潜力越大的邻居节点越靠近链表头部；若是两跳邻居则从链表尾部开始插入，具体插入顺序以邻居节点簇头潜力排列，潜力越大的邻居节点越靠近链表尾部。

上述的邻居节点插入规则有如下优点：节点两跳范围的最佳簇头节点在邻居表第一个元素、邻居表的最后一个元素及节点本身这 3个节点中诞生，而不必遍历整个邻居表，效率更高。

2.3 分簇算法描述

CACWC以节点能量及节点两跳内邻居的布局作为选择簇头的量化指标，该算法在各节点分布式地执行。各节点根据本地信息按需执行分簇算法，具有较强适应性。

分簇算法步骤的描述如下：

(1)若节点簇状态CS为−1，则分簇算法开始。

(2)广播Hello消息，根据收到的Hello消息响应更新本地邻居表。

(3)比较邻居表的第一个节点S1、最后一个节点Sn及节点本身S，选择最适合的节点为簇首。如果该簇首与S的距离为两跳，则只要 S存在某一条邻居作为中间节点到达该簇首(该中间节点可为其他簇的簇内节点)，该簇首就合法。三者按簇头潜力规则进行比较排列：

1)若节点S本身当选簇首，则更新本地节点信息，并广播更新报文。

2)若节点选择加入现有簇，则发送请求报文至簇首C，如果收到节点C的确认报文，则更新本地节点信息，并广播更新报文。

3)若节点选择未加入簇的节点 N为簇首，则发送请求报文至节点N，若收到节点N的确认报文，则节点更新本地节点消息，并广播更新报文

若节点发出请求报文，最终未收到确认报文，则执行步骤(4)。

(4)选择次优的节点作为簇首，并执行步骤(3)。

(5)节点收到请求报文，若节点当前处于未加入簇状态，则更新节点本地信息，将自己置为簇首，并发送确认消息至源节点；若节点当前为簇首，则判断自己能否纳入新成员，若能则更新本地邻居表，并发送确认消息至源节点。

2.4 簇的维护

簇的维护内容如下：

(1)簇首丢失

若簇成员发现簇头在两跳范围内不可达，则将自己的簇状态(CS)置为−1，自发执行分簇算法。

(2)中间节点连接丢失

若距离簇首两跳距离的节点发现当前到达簇首的中间节点不可达，则将搜索邻居表中到达簇首的中间节点链表，并选择其中一个节点作为到达簇首的中间节点(中间节点可以属于其他簇)，更新节点本地信息，若不存在到达簇首的中间节点则按簇首丢失处理。

(3)孤立簇首节点的处理

孤立簇首节点是指无簇成员的簇首[12]。孤立簇首每隔一段时间将自己的簇状态置为−1，并进行分簇算法，若选自己为簇首，则进行二进制指数退避算法延迟一段时间再次将自己的簇状态置为−1，直至有其他节点加入本簇或经过分簇算法选择其他节点作为簇首。

3 分析与证明

下面采用非形式化的证明方法，证明CACWC的正确性和优越性：

(1)CACWC中节点查找候选簇头的时间复杂度为常数。证明：CACWC中构造了如图 3所示的十字链表结构的两跳邻居表，按照提出的邻居表的构造规则，簇头潜力最大的一跳邻居位于纵向链表头部，簇头潜力最大的两跳邻居位于纵向链表的尾部。而纵向链表为双向链表结构，故获取最佳候选簇首(最佳候选包含节点本身)的时间复杂度为O(1)。证毕。

(2)算法最坏情况下时间复杂度是O(n2)，n为节点规模。证明：假设网络规模为n，第i个节点的两跳范围内邻节点数为Ni，且由算法保证每个节点至多发送2条消息就可完成分簇过程，因此，第i个节点至多发送的消息条数为2×Di，则全网完成分簇至多发送的消息条数为所以，算法最坏情况下时间复杂度为证毕。

(3)兼容弱连通簇的 Ad Hoc网络中的孤立簇首数不大于强连通簇结构的Ad Hoc网络。证明：先由节点选择簇首的角度分析。在兼容弱连通簇的网络中，簇首选自邻接表纵向链表的首部、尾部以及节点本身。先假设三者当选簇首的概率分别为 Phead、Ptail、Pself，且满足 Phead+Ptail+Pself=1。设强连通簇结构的网络中对应的概率分别为 Phead’、Ptail’、Pself’，且满足 Phead’+Ptail’+Pself’=1。由于强连通簇要求簇内成员到簇首的中间节点也属于该簇，而兼容弱连通簇的网络则无该强制条件，因此有 Ptail≥Ptail’，则有 Phead+Pself≤Phead’+Pself’。在其他因素保持不变的情况下，Pself≤Pself’，即在兼容弱连通簇的条件下，节点自身当选簇首的概率更小，即最多相等(结论1)。

现由节点已成为簇首的角度分析。假设节点N两跳邻居内包含簇首节点H，且两者距离为Distance(N,H)=2。在强连通簇结构中，若节点 N、H之间无节点 V满足Distance(N,V)=1且 Distance(V,H)=1(节点V∈CH)，则 N 将不会选择节点H作为簇首。相反在弱连通簇结构下，只要存在任一节点U满足Distance(N,U)=1，且Distance(U,H)=1，节点N即可能选择H作为簇首。因此，兼容弱连通簇的网络中簇首节点获得簇成员的概率更小，即最多相等(结论2)。

综合结论1、结论2可知，在其他因素不变的情况下，兼容弱连通簇的 Ad Hoc网络选择自己单选簇头的概率相对更小，且更容易吸收簇成员，故孤立簇首数不大于强连通簇结构的Ad Hoc网络。证毕。

(4)兼容弱连通簇的 Ad Hoc网络比强连通的网络具有更优的稳定性。证明：由证明(3)可知，兼容弱连通簇的Ad Hoc网络孤立簇首数不大于强连通簇结构的Ad Hoc网络，因此，在其他条件不变的情况下，兼容弱连通的网络中簇结构分布更加均衡。此外，在兼容弱连通簇的条件下，节点无强连通的限制，节点在两跳范围内簇首的候选更多，且根据簇头潜力规则选择最优节点作为簇首。最优节点具有能量、拓扑等方面的优势，有效存活时间更长。因此，兼容弱连通的Ad Hoc网络负载更加均衡，并具有较好的持续性和稳定性。证毕。

4 结束语

本文提出一种兼容弱连通簇的Ad Hoc网络分簇算法。在两跳范围内允许弱连通簇存在，簇结构不以主宰域为基础，因此，节点能够选择更适合的节点作为簇首，并降低节点改变簇首的次数，使簇结构更加稳定。分析结果表明，该算法限制了簇成员个数，防止生成过大的簇，避免了簇首资源过快消耗，使得簇的有效存活时间更长。对整体网络而言，尽可能地减少了孤立簇首节点的出现，优化了网络的簇划分。然而，在CACWC算法的实现中，分簇算法仅考虑了两跳范围的簇，邻居表的设计扩展性较差，在面临诸如三跳及以上的簇结构时，邻居表的维护开销过大，明显影响算法的效果。因此，如何设计一个合理的可扩展邻居表结构是今后的研究方向。

[1]王海涛.移动Ad Hoc网络的分簇算法及性能比较[J].北京邮电大学学报,2004,27(1): 93-97.

[2]Richard C L,Mario G.Adaptive Clustering for Mobile Wireless Networks[J].IEEE Journal on Selected Areas in Communications,1997,15(7): 1265-1275.

[3]Jane Y Y,Petr H J.A Survey of Clustering Schemes for Mobile Ad Hoc Networks[J].IEEE Communications Survey and Tutorials,2005,7(1): 32-48.

[4]Dai Fei,Wu Jie.On Constucting K-connected K-dominating Set in Wireless Network[C]//Proc.of the 19th IEEE International Parallel and Distributed Processing Symposium.[S.l.]: IEEE Press,2005.

[5]杨卫东.考虑节点能量状态的 Ad Hoc网络分簇算法[J].计算机工程,2010,36(12): 119-122.

[6]张 丽,余镇危,张 扬.移动Ad Hoc网络的一种自适应权值分簇算法[J].西安电子科技大学学报: 自然科学版,2008,35(3): 572-576.

[7]Drira K,Lyon D,Kheddouci H.A New Clustering Algorithm for MANETs[C]//Proc.of the 14th International Telecommunications Network Strategy and Planning Symposium.[S.l.]: IEEE Press,2010.

[8]Zheng Chan,Yin Ling,Sun Shixin.Construction of D-hop Connected Dominating Sets in Wireless Sensor Networks Procedia Engineering,2011,15: 3416-3420.

[9]Cokuslu D,Erciyes K.A Hierarchical Connected Dominating Set Based Clustering Algorithm for Mobile Ad Hoc Networks[C]//Proc.of IEEE International Symposium on Modeling Analysis and Simulation of Computer and Telecommunication Systems.Istanbul,Turkey: [s.n.],2007.

[10]Xu Kaixin,Hong Xiaoyan,Gerla M.An Ad Hoc Network with Mobile Backbones[J].IEEE International Conference on Communications,2002,5: 3138-3143.

[11]Chatterjee M,Das S K,Turgut D.WCA: A Weighted Clustering Algorithm for Mobile Ad Hoc Networks[J].Cluster Computing,2009,5(2): 193-204.

[12]Srivastava S,Gohsh R K.Distributed Algorithms for Finding and Maintaining a K-tree Core in a Dynamic Network[J].Information Processing Letters,2003,88(4): 187-194.