一种基于同心圆切割的XML编码方案
2013-08-17郭丽红
郭丽红,王 箭,杜 贺
(1.南京航空航天大学计算机科学与技术学院,南京 210016;2.南京工程学院通信工程学院,南京 211167)
1 概述
随着(eXtensible Markup Language,XML)文档被广泛应用,Internet上出现了大量用可扩展标记语言XML文档来描述的信息,如何有效地管理和查询这些网上海量的XML信息,已经成为学者们近年来研究的课题[1-2]。在 XML众多研究问题中,XML文档节点编码在XML研究中有着基础性的重要作用。
为 XML文档树中的节点分配唯一编号的具体策略称为XML节点编码方案。为高效地支持XML数据的查询,一个高效的编码方案应能快速高效地判定任意 2个节点间的结构关系,包括父子关系、兄弟关系、祖先后代关系等,而且也能快速定位某一具体节点所在位置。本文侧重于XML数据编码中区间编码方案的研究,针对目前XML区间编码方案中的主要问题进行分析,在现有的区间编码方法的基础上,提出一种新的高效的编码方法。
2 相关研究
目前,对XML文档树的编码已有很多研究,如位向量编码[3]、前缀编码[4]、区间编码[5]、素数编码等[6]。本文主要针对几种常见的区间编码方法进行研究与分析,为新编码方案的提出打下基础。
2.1 常见的区间编码方法
区域编码方法是为每个节点分配一对隐含该节点包含区域的数字。给定任意2个区域z1和z2,如果称z1包含z2,则z1节点是z2节点的祖先。目前常见的区域编码分为基本区域编码和扩展区域编码。为描述方便,本文以下部分用L(u)表示节点u的编码。
(1)Dietz区间编码
Dietz区间编码[7]的编码规则是树T的每一个节点都被赋予一个含有先序遍历序号和后序遍历序号的二元组节点,可以表示为(preorder,postorder)。前序遍历XML树时节点对应的前序遍历值用preorder表示,后序遍历XML树时节点对应的后序遍历值用postorder表示。
(2)起止区间编码
节点的起止区间编码[8]可以用一个三元组来表示:(start,end,level)。该节点在文档结构树中的起始位置用start表示,结束位置用end表示,节点所处的层次用level表示,start和end可以看作是深度优先遍历该节点所在的XML树,进入该节点用start表示,离开该节点用end表示,每次访问一个节点时,依次分配一个整数。
(3)扩展的区域编码
节点的扩展区域编码[9]是一个三元组,可以表示为(order,size,level),order和size分别表示该节点的前序遍历顺序和该节点的大小,level表示节点所处的层次。用该方法对节点进行编码的时候可使 size适当大于该节点的实际大小,这样可以为插入新节点预留空间,减少更新的代价。
2.2 区间编码方法举例
图1是一棵具体的XML文档树,对于树的层数的定义,这里规定,树根所在的层数为0,它的孩子节点所在层数1,依次向下递增。具体的相对于这棵XML树的Dietz区间编码、起止区间编码和扩展区间编码的信息如表1所示。

图1 原始XML树

表1 原始XML树的区间编码
3 基于同心圆切割的XML编码
XML文档是由树型结构来表示的,对n层树,如果把树根看作成圆心,树的每一层节点各自分布不同半径的多个同心圆上,那么这棵倒置的树更像一个以根节点为圆心由多个半径不同的同心圆组成的一个同心圆集合,而这些分布在若干个同心圆上的节点,像是在这些同心圆上进行区域分割,基于该设想,本文提出一种同心圆切割的XML编码方案。
3.1 编码的构建
基于上述同心圆切割的理论,把XML树中每个节点编码成两部分组成(RX,agl)。
(1)组合标识RX
R代表节点所在的同心圆集合中所在圆的半径,也代表该节点在树中所处的层数,从树根开始层数逐渐上升,其中根节点所在半径为0,其儿子节点所在半径为1,依次以1为步长递增。X代表组标识,规定兄弟节点分在同一组内,具有相同的组标识。这里组标识选用字母来标识,依次可以为 a,b,c,…,z,aa,ab,…,az,ba,bb,bc,…,ca,…。
(2)角度agl
由于采用同心圆平均切割理论,任意节点的孩子节点是平分该节点所占有区域的,因此每个节点都占据圆中的一个区域,这里选用起始角度 agl代表该节点。针对图 1原始XML树的同心圆切割编码如图2所示,其中,A为根节点即圆心节点,编码为(0,0),A的3个孩子节点,属于同一组,组编码采用字母编码,因此,其组编码为a,三节点平分半径为1的圆,其中第1个孩子从0°开始(水平方向),每个节点占据 360°/3=120°的区域,B 占据[0,120°),C 占据[120°,240°),D 占据[240°,360°)的半开半闭区间。节点编码以起始角度为准,因此,B的编码为(1a,0),C的编码为(1a,120°)。同理,对于C的孩子节点E、F、G,这3个节点安置于C的[120°,240°)范围内,但其位于半径为2的圆内,每点主要占据40((240°,120°)/3)的区域,因此,E的编码为(2a,120°),F 的编码为(2a,160°),G 编码为(2a,200°),依次继续编码,图2的具体编码如表2所示。XML文档树的分布连接关系如图3所示。
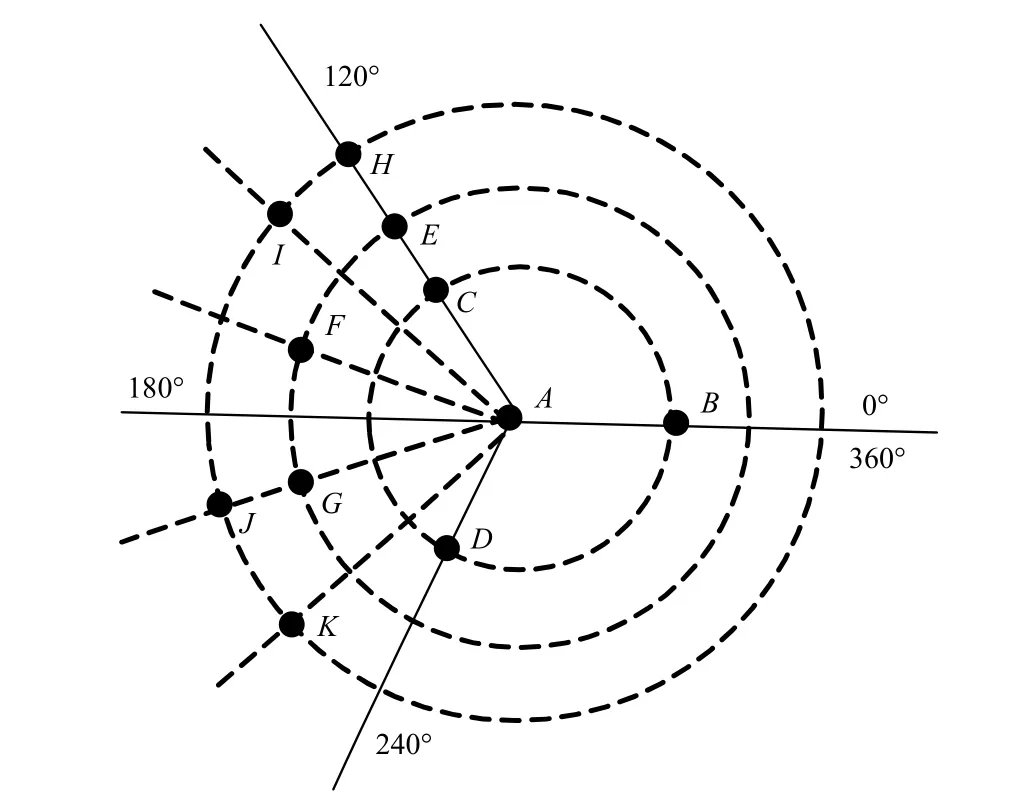
图2 同心圆切割编码后节点分布位置

表2 同心圆切割编码
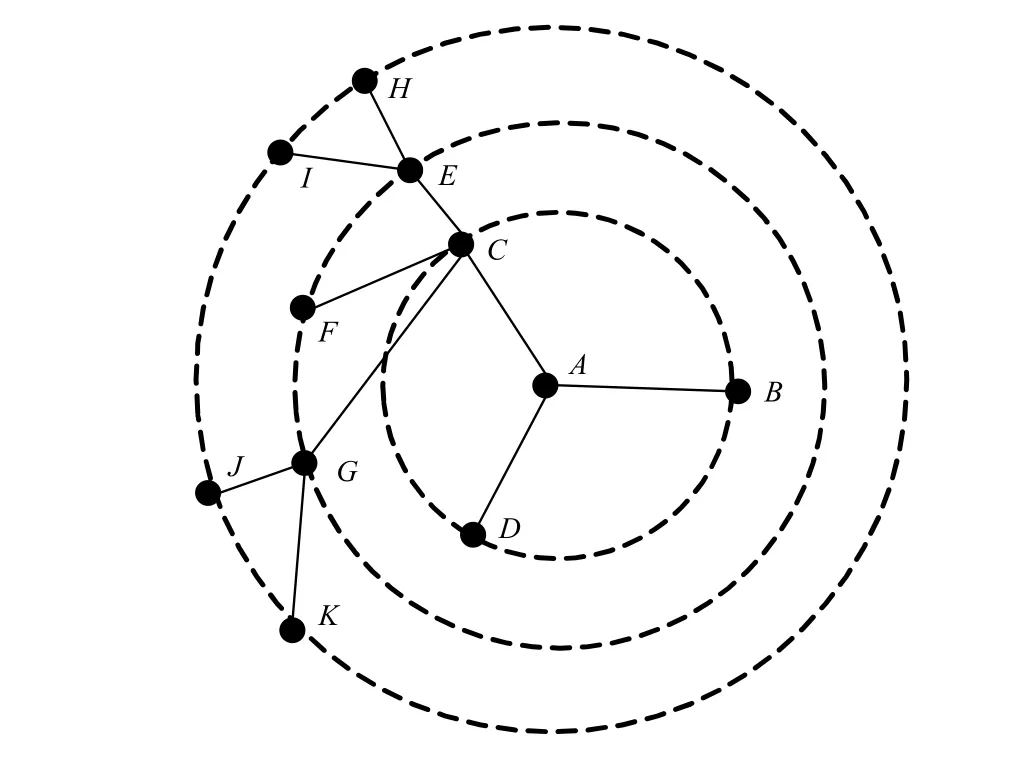
图3 XML文档树在同心圆中的分布连接关系
3.2 节点关系判定法则
节点关系的判定法则如下:
(1)父子关系的判定
对于节点u和v,如果节点u存在右兄弟节点u’,当且仅当 L(u).agl (2)兄弟关系的判定 对于节点u和v,当且仅当L(v).RX=L(u).RX,u和v是兄弟节点。 (3)祖先后代关系的判定 对于节点u和v,如果节点u存在右兄弟节点u’,当且仅当 L(u).agl 为测试新编码方案的时空效率,本文主要比较Dietz区间编码、起止区间编码(Start End,简称StartE)和本文的同心圆切割的编码方案(Concentric Circular Cutting,简称3C)。本文实验是在处理器为Intel Pentium 43.02 GHz,内存为1 GB,操作系统为Windows XP环境下采用Visual C++6.0,基于 DOM 技术编程实现的。实验所采用的测试文档由 XML自动生成工具 XMark[10]生成,文档树的最大深度和平均深度等信息如表3所示。 表3 XML测试数据集 从图4中数据和表1信息可以看出,Dietz方案在文档的节点数比较少时,所占据的存储空间比较小,而随着文档节点数的增加,编码空间越来越大,这是因为节点数小于65535时,每个节点占用4 Byte空间,而超过65535,则需要8 Byte编码;StartE编码方法在节点数小于32767时,每个节点占用5 Byte空间,而超过32767,则需要9 Byte编码;3C编码与节点的分布及其扇出度相关,在多数情况下每个节点占用 6 Byte空间,具体信息如图 4所示。 图4 编码空间 图5是上述3种方案在编码时间上的对比,从测试数据可以看出,Dietz区间编码时需要2次遍历XML文档,很明显地,这2种方法在编码时间上比较耗时,StartE方法除了遍历上费时之外,时间主要耗费在第 2次访问编码节点时的判断上,但是整体编码时间略低于Dietz方法;而 3C方法整体遍历一次,标识简单,因此,编码时间最小。 图5 编码时间 本文对目前典型的区间编码方法进行分析,提出一种基于同心圆切割的节点编码方案。该方案在文档较大、节点个数比较多的情况下,可改善查询效率和编码时空效率,为XML其他处理做基础性的准备,因此,该方案对于较大文档的查询有一定的使用及借鉴价值,此外,把XML树中节点布局到同心圆中,可以利用数学的理论和方法来求各节点之间的关系,包括对节点的具体定位、求某节点的子孙后代等,这是下一步的研究方向。 [1]荆旦建.基于XML的数据管理技术的研究[D].南京: 南京理工大学,2009. [2]孟小峰,王 宇,王小锋.XML查询优化研究[J].软件学报,2006,17(10): 2069-2086. [3]Mohammad S,Martin P.LLS: Level-based Labeling Scheme for XML Databases[C]//Proceedings of 2010 Conference of the Center for Advanced Studies on Collaborative Research.New York,USA: [s.n.],2010. [4]An D,Park S.Efficient Access Control Labeling Scheme for Secure XML Query Processing[J].Computer Standards &Interfaces,2011,33(5): 439-447. [5]Niu Na,Dong Guoqing.A New Labeling Scheme for XML Trees Based on Mesh Partition[C]//Proceedings of the 2nd International Conference on Future Computer and Communication.New York,USA: [s.n.],2010. [6]Lu Jiaheng,Meng Xiaofeng,Tok W L.Indexing and Query XML Using Extended Dewey Labeling Scheme[J].Data &Knowledge Engineering,2011,70(1): 35-59. [7]Dietz P F.Maintaining Order in a Linked List[C]//Proceedings of the 14th Annual ACM Symposium on Theory of Computing.San Francisco,USA: ACM Press,1982. [8]Zhang Chun,Naughton J F,DeWitt D J,et al.On Supporting Containment Queries in Relational Database Management Systems[C]//Proceedings of the 27th ACM SIGMOD.Santa Barbara,USA: ACM Press,2001. [9]Yun J H,Chung C W.Dynamic Interval-based Labeling Scheme for Efficient XML Query and Update Processing[J].Journal of Systems and Software,2008,81(1): 56-70. [10]Schmidt A R.XMark——An XML Benchmark Project[EB/OL].[2012-06-03].http://monetdb.cwi.nl/xml/index.html.4 实验分析与比较

4.1 编码空间对比
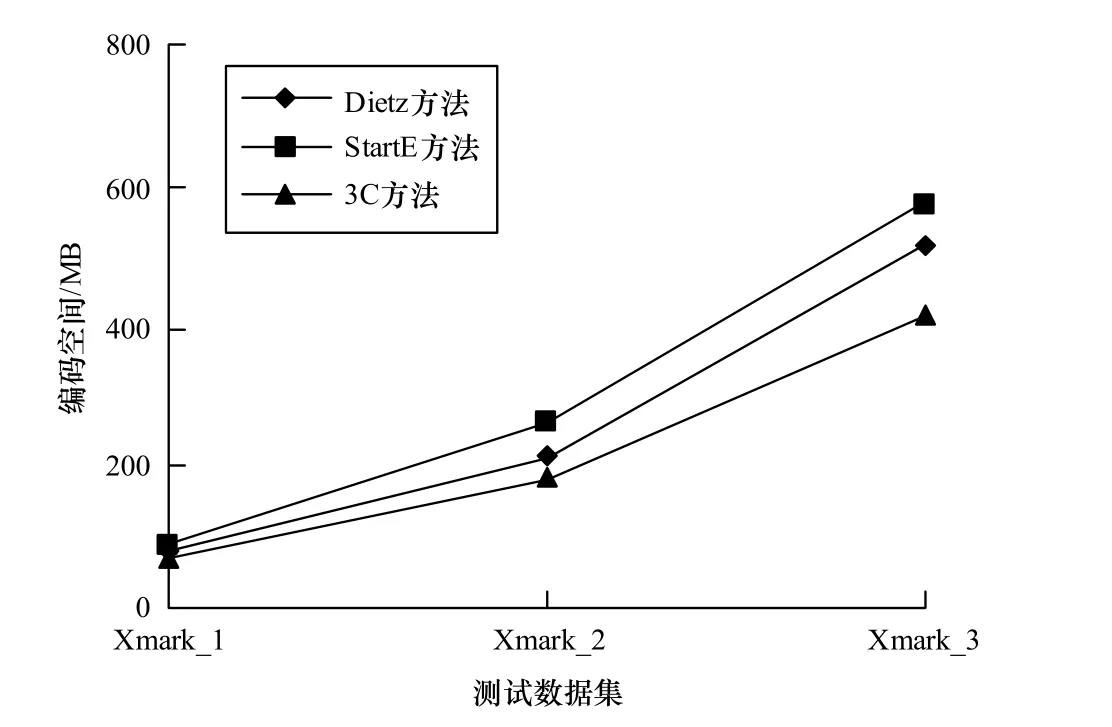
4.2 编码时间对比
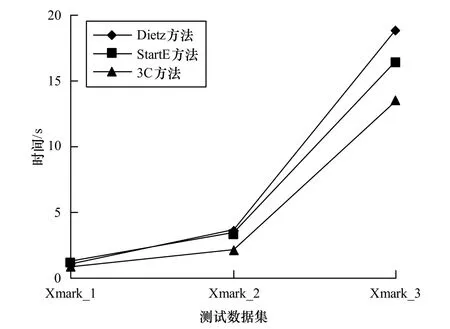
5 结束语
