随机利率情形下的梯式期权定价模型

冯增辉，薛 红，王晓东

(西安工程大学 理学院，西安710048)

金融市场的快速发展，促进了许多奇异期权的出现[1]，而梯式期权是一种较为复杂的奇异期权，这种期权除了设定行使价外，还同时设有多个“梯级价”，只要标的资产的价格触及某一梯级价，就可锁定一定水平的获利[2－7].文献[1]假设股票价格遵循布朗运动驱动下的随机微分方程，利用有限[0，T]区间上的具有漂移的布朗运动的最大值分布及其与终值的联合分布，用鞅方法得到了利率为常数的梯式期权定价公式.文献[2]用鞅方法讨论了随机利率情形下多维Black－Scholes定价模型，得到了随机利率情形下的欧式期权以及交换期权定价公式.本文利用风险中性概率测度和在有限[0，T]区间上的具有漂移的布朗运动的最大值及其终值的联合分布，得到了随机利率情形下的梯式期权定价公式，将文献[1]做了推广.

1 金融市场数学模型

考虑如下模型:假设金融市场的两种资产，一种是股票，其价格满足

另一种是债券，其价格满足

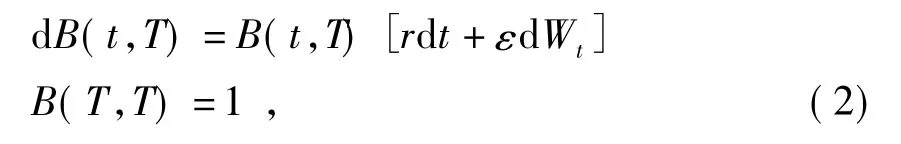
其中:r为无风险利率，ε为债券波动率，μ为期望收益率，σ 为股票波动率.{Wt，0≤t≤T}为概率空间(Ω，F，P)上的标准布朗运动.

考虑时间区间[0，T]，设α，β分别表示零时刻投资者拥有股票和债券数目，则财富过程满足所以

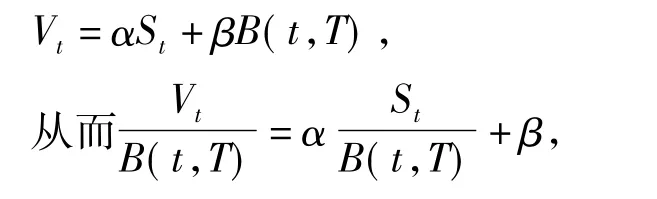
利用Ito引理

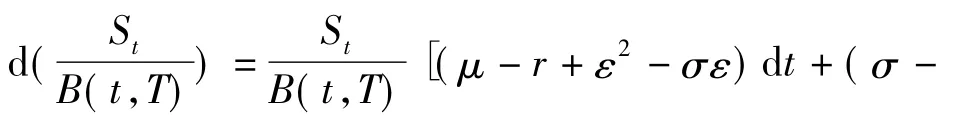
记 μ－r+ε2－σε=(σ －ε)θ，定义的概率测度

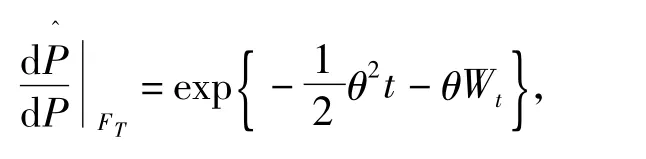
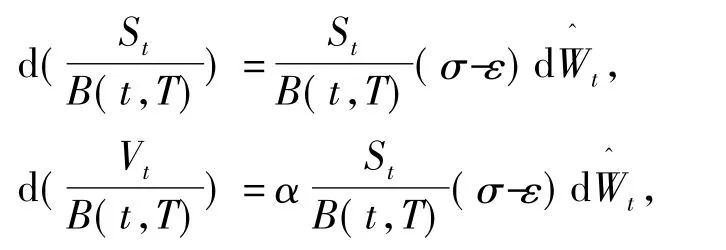
即:

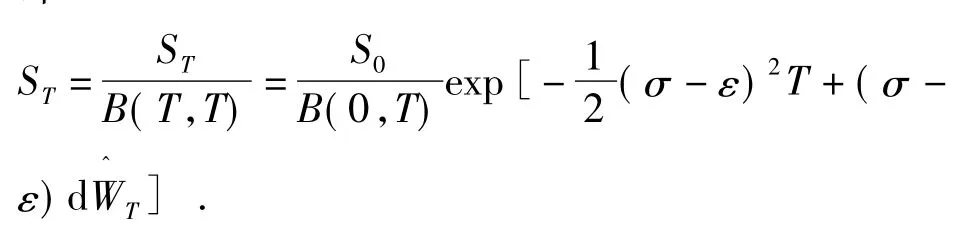
定理1[2]在金融市场中，欧式未定权益g(ST)在零时刻的无套利价格为

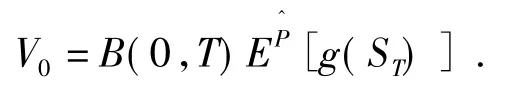
2 梯式期权定价公式

引理 2[1]设 Yt= μt+σWt，(0≤T≤T)，其中:μ为常数，σ≠0，设则 YT与T的联合分布密度f(x，y)为

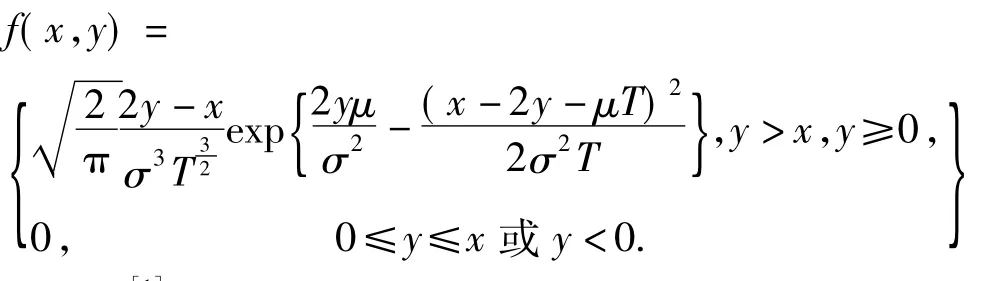
定义3[1]梯式看涨期权是具有以下可能收益的奇异期权，

1)当L＞K时，梯式看涨期权的收益为:

max[ST－K，L－K]如果 S在期权终止前达到L，

max[ST－K，0] 否则.

2)当L≤K时，则梯式看涨期权的收益化为Black－Scholes看涨期权的收益.

定理4 梯式看涨期权在零时刻的无套利价格为

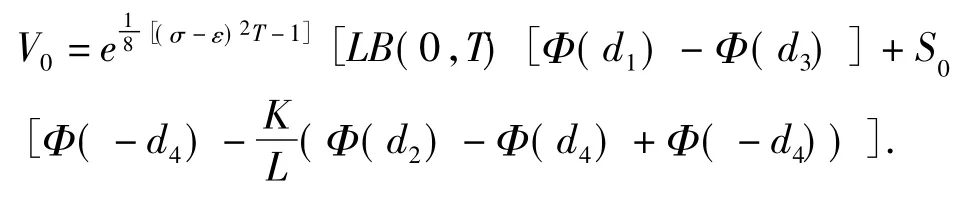
其中

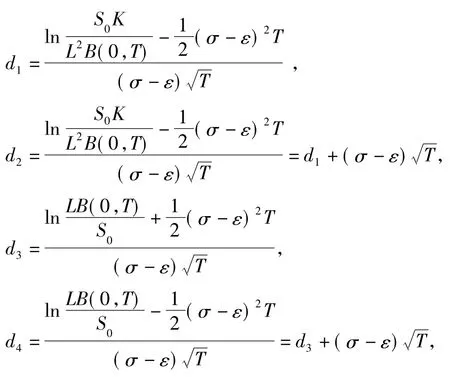
同理可得

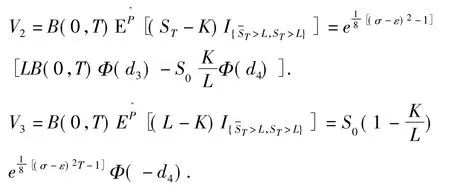
再由简单的代数运算就可得出结论.

[1] 王 铁，王 威.布朗运动的最大值和阶梯期权[J].经济数学，2006，23(1):46 －51.

[2] 薛 红.随机利率情形下的多维Black－Schols模型[J].工程数学学报，2005，22(4):645 －652.

[3] 程希骏.金融资产定价理论[M].合肥:中国科学技术大学出版社，2006:126－139.

[4] 薛 红.在随机利率情形下有红利支付的股票未定权益定价[J].西北纺织工学院学报，2000，14(1):57 －61.

[5] 吴永红，李 琼，金 勇.随机利率下的外汇欧式期权定价[J].武汉理工大学学报，2011，35(5):1020 －1023.

[6] 张凯凡.鞅方法在股指期权定价中的应用[J].湖北工业大学学报，2011，26(5):96－98.

[7] 蔺 捷，薛 红，王晓东.分数布朗运动环境下缺口期权定价模型[J].哈尔滨商业大学学报:自然科学版，2012，28(5):616－619.