关于素环的导子

杜君花，王 立

(1.齐齐哈尔大学理学院，黑龙江齐齐哈尔161006;2.哈尔滨理工大学应用科学学院，哈尔滨150080)

1 引言及引理

自Posner在文献[1]中讨论了素环和半素环上导子的几个问题后，许多人在这方面进行了研究.1957年Posner首先证明具有中心化的非零导子的素环一定是可换环，1984年Mayne在文献[2]中推广了Posner定理，讨论了对任意x∈I均有[x，d(x2)]∈Z的情况.1994年在文献[3]中又讨论了任意的x∈I均有[x，d(x2)]∈Z的情况，但没有讨论的[x，d(x2)]∈Z 情况和x2◦d(x)∈Z 且Z∩I≠{0}的情况.本文针对这两种情况进行讨论，得到了环R交换的一些新的条件.

假定R是结合环，d是环R到自身的一个映射.如果对任意的x，y∈R，有 d(x+y)=d(x)+d(y)且d(xy)=xd(y)+d(x)y，则称 d是 R的导子.xy－yx称为换位子，记作[x，y]，xy+yx称为反换位子，记作x◦y.

本文中的环均为结合环，用Z表示环R的中心.

引理1[3]设R是特征不为2的素环，I是R的非零理想，若存在非零导子d，满足对任意的x∈I均有[x，d(x2)]∈Z，则 R 环为交换环.

引理2[4]若 Z为环R的中心，d为 R的导子，则d(Z)⊆Z.

2 主要结论及证明

定理1 设R是6－扭自由的素环，I是R的非零理想，Z是环R的中心，若存在非零导子d满足对任意的x∈I均有[x，d(x2)]∈Z，则环R为交换环.

证明 若存在0≠c∈Z∩I，则对任意的x∈I，用 c+x代[x，d(x2)]∈Z 中的x，有

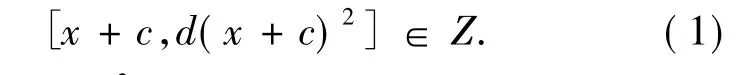
又c∈Z可知d(c2)∈Z，即有

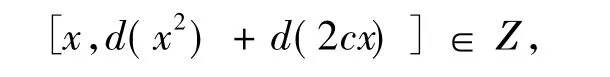
又[x，d(x2)]∈Z，R 是6－扭自由的素环，故有

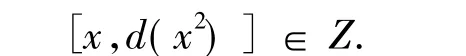
由引理可知环R交换.

若Z∩I={0}即有

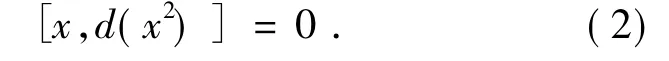
对任意的 x∈I、y∈I，用 x+y 代替式(2)中的 x，可得

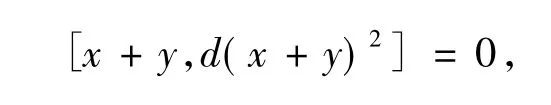
整理有

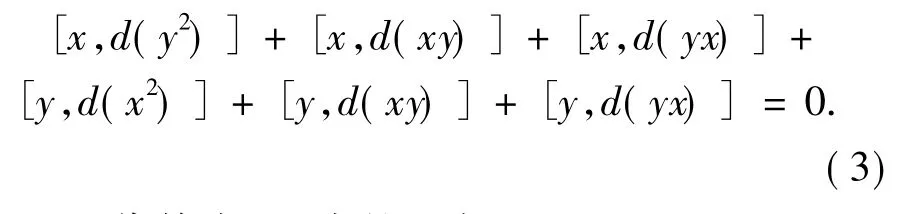
用x－y代替式(2)中的x有

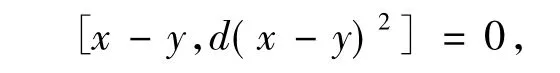
整理有

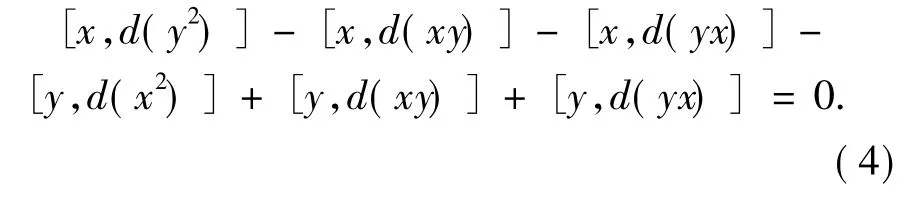
式(3)+式(4)可得

2([x，d(y2)]+[y，d(xy)]+[y，d(yx)])=0.又R是6－扭自由的素环，故得

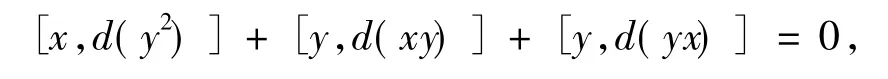
展开可得

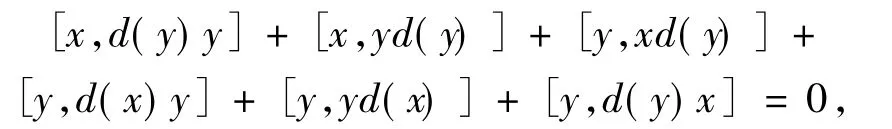
进而可得

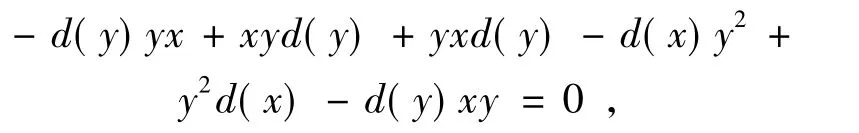
即

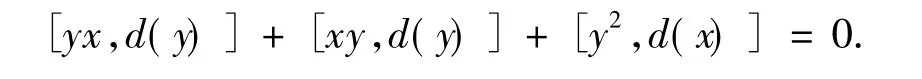
用x代替上式中的y有

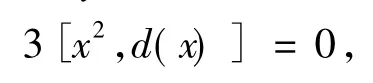
又R是6－扭自由的素环，可得

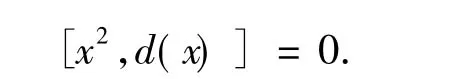
由引理可知环R为交换环.

定理2 设R是6－扭自由的素环，I是R的非零理想，Z是环R的中心，若存在非零导子d满足对任意的x∈I均有x2◦d(x)∈Z且Z∩I≠{0}，则环R为交换环.

证明 用x+y代替x2◦d(x)∈Z中的x有

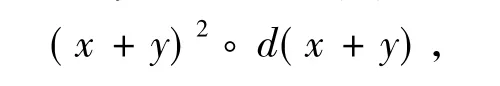
即

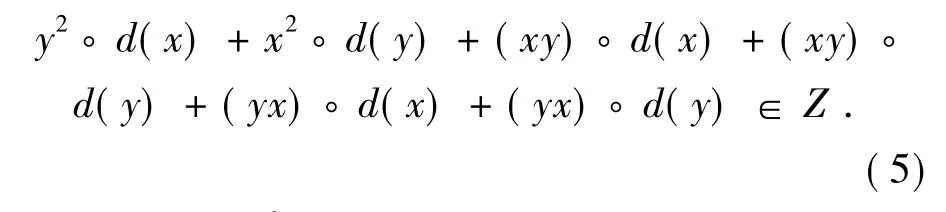
用x－y代替x2◦d(x)∈Z中的x，可得

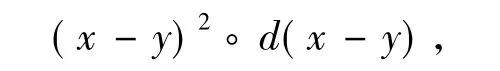
即

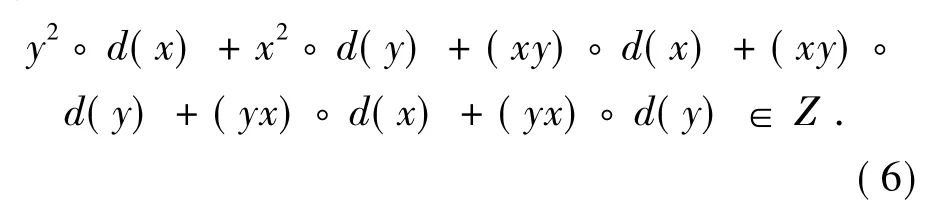
式(5)+式(6)，得

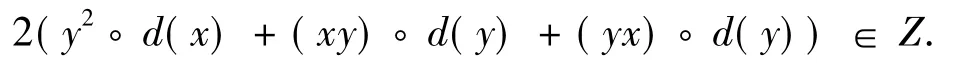
又R是6－扭自由的，故有

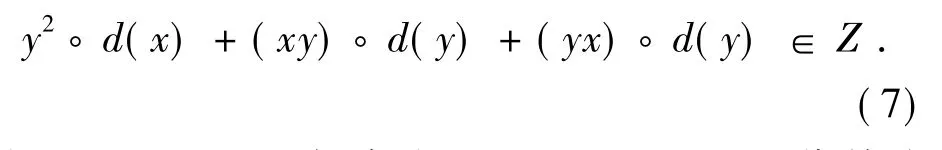
由Z∩I≠{0}可知存在0≠c∈Z∩I，用c代替式(7)中的 x，可得

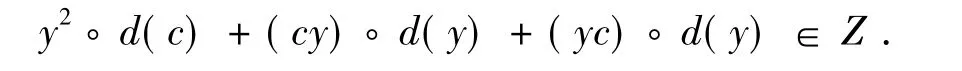
由已知可得

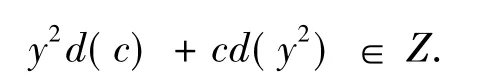
于是∀y∈I均有

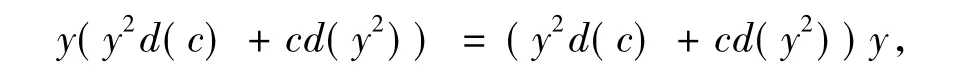
即

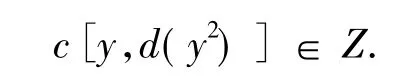
又 c∈Z，故有

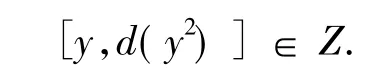
由定理1可知环R交换.

[1] POSNER E C.Derivations in prime rings[J].Proc.Amer Math Soc.，1957，8:1093 －1100.

[2] MAYNE J.Centralizing mappings of prime rings[J].Canad Math Bull.，1984，279:122 －126.

[3] HUANG Y B，ZHU L S.On derivation of prime rings[J].(PRC)of Math.，1994，4:579 －586.

[4] 王 宇，张秀英.素环上中心化广义导子[J].东北师范大学报:自然科学版，2001，33(2):116 －118.