Mann迭代算法求解非线性混合隐变分不等式

向国坤，冯世强，李 伦

(西华师范大学数学与信息学院，四川南充637002)

1 引言

在当今数学的很多领域里，变分不等式理论是一个非常强大的工具[1－5].近年来，特别是，古典变分不等式问题在力学、物理学、优化与控制、非线性规划、经济学和交通平衡和工程科学等学科领域里有着广泛的发展和应用[6－7].

众所周知，研究变分不等式理论最重要和最困难的问题之一就是发展一种高效的、可实现的迭代算法.这类迭代算法可以用来解决各类变分不等式和变分包含问题.这类迭代算法中用到的投影和收缩方法以及它的各种变形形式是求解各种类型变分不等式和互补问题近似解的重要工具.一般情况下，这类迭代算法中用到的投影和收缩方法的收敛性分析通常需要映射必须是强单调或者满射.像这样严格的限制条件制约了我们用投影和收缩方法来解决很多应用型问题.因此，这个事实告诉我们有必要对投影和收缩方法做进一步的优化工作[7－8].

结合文献[5]中所提到的一类投影收缩算法及相关性质来求解变形的变分不等式问题和文献[9]中求解一类非线性混合隐变分不等式的迭代算法.本文用一种新的Mann迭代算法来求解一类非线性混合隐变分不等式.在这个过程中，我们用到了预解算子和对Mann迭代算法所产生的迭代序列进行了收敛性分析.本文的映射A既不是强单调映射，也不是满射，有利于投影和收缩法在许多领域里的应用和发展.

2 预备知识

假设一个单值映射A∶Rn→Rn，和一个适当的凸下半连续映射φ∶Rn→Rn∪{+∞}.本文考虑以下的一个非线性混合隐变分不等式问题.

令 a∈Rn，使得

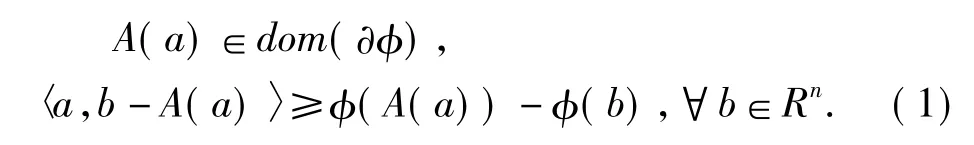
如果φ=δk，其中δk表示一个非空闭凸集K的指示函数.这样，问题(1)就等价于找到一个a∈Rn，使得 A(a)∈K，

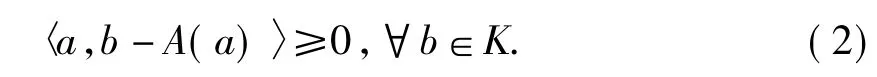
我们把(2)中的不等式问题叫做非线性隐变分不等式问题.

为了求得非线性隐变分不等式问题的解，首先，我们需要引入以下概念和引理.

定义2.1 如果A∶Rn→Rn的一个映射，并且存在一个常数ξ＞0，满足以下条件‖A(a)－A(b)‖≤ξ‖a － b‖，∀a，b∈Rn.

那么，映射A就称作Lipschitz连续.

定义2.2 如果A∶Rn→Rn的一个映射，同时满足以下条件〈A(a) －A(b)，a－b〉≥0，∀a，b∈Rn

那么，映射A就称作单调映射.

定义2.3 如果 φ∶Rn→Rn∪{+∞}的一个凸下半连续泛函，∂φ表示φ的一个次微分，常数ρ＞0，那么，定义一个预解算子(b)∶Rn→Rn.(b)=(I+ ρ∂φ)－1(b)，∀b∈Rn.

备注2.1[7]如果 δk表示一个非空闭凸集 K的指示函数，Pk表示一个投影映射，当φ=δk时，我们可以得到:是非扩张的，并且=Pk.

引理 2.1[8]给定一个点 a∈Rn，当 a=(c)时，任意一个点c∈Rn满足如下的不等式

引理2.2 如果 φ∶Rn→Rn∪{+∞}的一个凸下半连续泛函，并且是预解算子，那么，可以得到:I－是非扩张的.

证明:对∀x，y∈Rn，根据引理 2.1，可以得到

引理2.3 如果映射A∶Rn→Rn的单调映射且映射A是关于Lipschitz常数ξ＞0的Lipschitz连续映射，令 λk∈(0，1]，常数 ρ＞0，当 λk=1 或者时，则可以得到 [2－(λk－1)2－

证明:当 λk∈(0，1]时，那么，我们可以得到

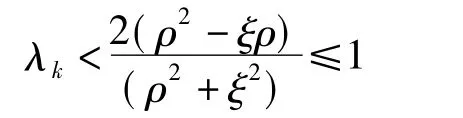
结论证毕.

3 迭代算法和收敛性分析

本节中，我们将用一种新的Mann迭代算法来求解问题(1)和问题(2).

如果映射A∶Rn→Rn的单值映射，映射φ∶Rn→Rn∪{+∞}的凸下半连续泛函，常数ρ＞0.

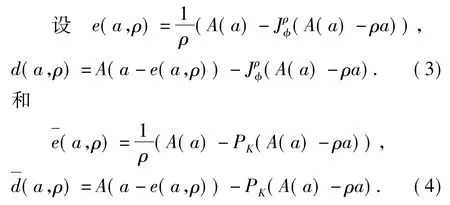
由引理 2.1和备注2.1可以知道，当 e(a，ρ)=0时，a∈Rn是问题(1)的一个解;当(a，ρ)=0时，a∈Rn是问题(2)的一个解.

为求解问题(1)的解，我们给出以下的Mann迭代算法[9].

算法3.1 对∀a0∈Rn定义一个迭代序列{ak}如下如果满足 φ=δk，那么，算法3.1可以得到如下变形.

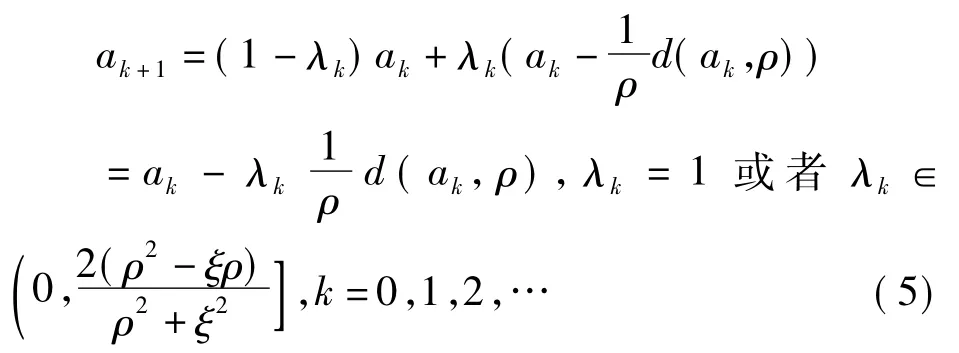
算法3.2对∀a0∈Rn，定义一个迭代序列{ak}如下

定理3.1 如果映射A∶Rn→Rn是一个单调映射，映射φ∶Rn→Rn∪{+∞}是一个凸下半连续泛函，那么，问题(1)的任意解a*∈Rn，满足以下不等式〈a － a*，d(a，ρ)〉≥〈e(a，p)，d(a，ρ)〉，

证明:设a*是问题(1)的一个解，由(1)式可以得到

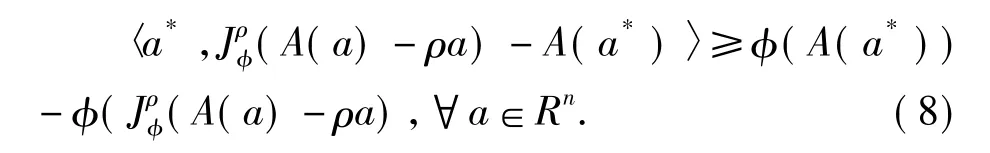
由引理2.1，我们可以得到

综合式(8)、(9)，可以得到

又因为A是一个单调映射，我们可以得到

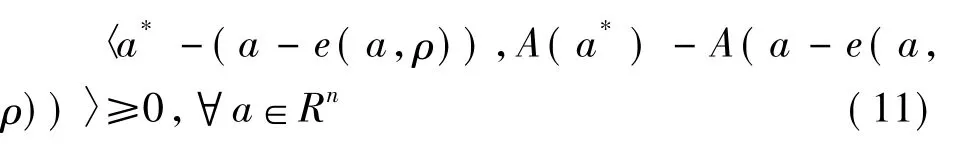
结合式(10)、(11)，可以得到变形得

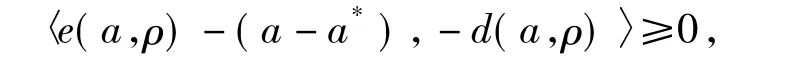
结论证毕.

定理3.2 如果映射A∶Rn→Rn的单调映射，并且映射A是关于Lipschitz常数ξ＞0的Lipschitz连续映射，序列{ak}是算法3.1中定义的迭代序列，那么，问题(1)的任意解a*∈Rn满足以下不等式

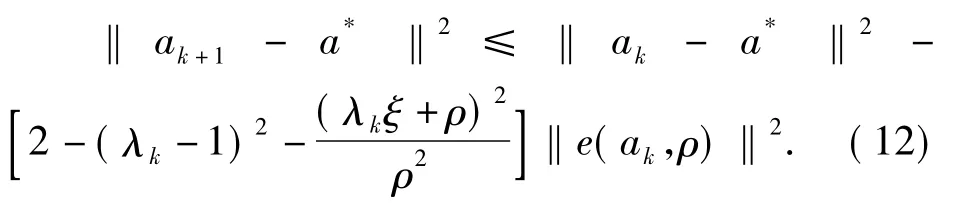
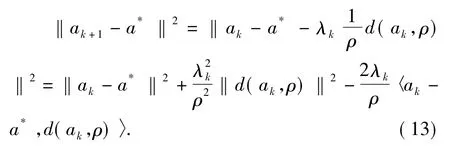
证明:设a*是问题(1)的一个解，由式(5)可以得到又因为映射A是单调的，并且Lipschitz连续.我们有由定理3.1可以得到

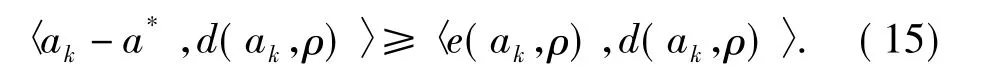
进一步可以得到

结论证毕.

当λk=1时，式(12)可以退化为文献[9]中的结论.

推论3.1[9]如果映射的单调映射 A∶Rn→Rn，并且映射是关于Lipschitz常数ξ＞0的Lipschitz连续映射，序列{ak}是算法3.1中定义的迭代序列，那么，当λk=1时，问题(1)的任意解a*∈Rn满足以下不等式

定理3.3 已知映射A∶Rn→Rn的单调映射，并且映射A是关于Lipschitz常数ξ＞0的Lipschitz连续映射，{ak}是算法3.1中定义的迭代序列，如果常数ρ＞(+1)ξ，那么，迭代序列{ak}收敛于问题(1)的一个解a*∈Rn.

证明:设a*是问题(1)的一个解，由定理3.2可以得到

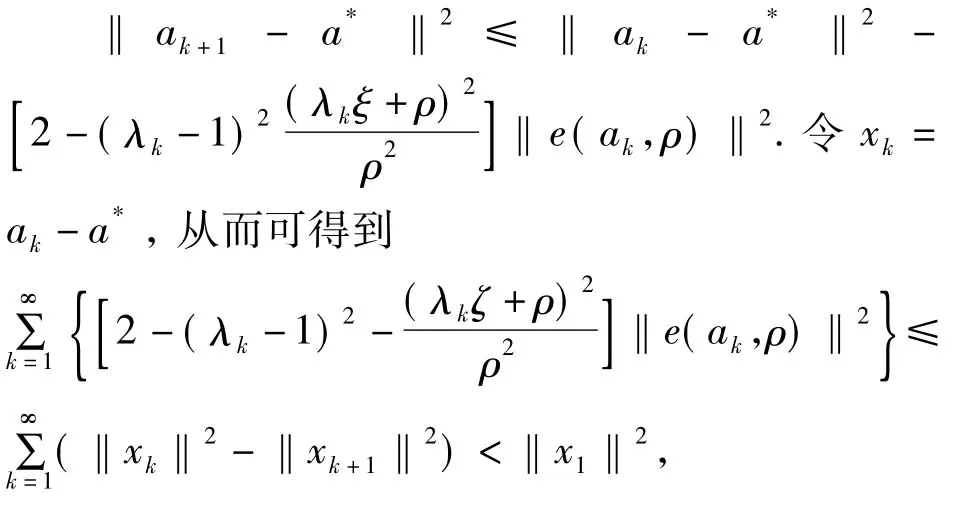
由引理 2.3可知，当 λk=1或者 λk∈时， 容 易 得 到进一步可得到:xk是单调递减的，迭代序列{ak}是有界的和e(ak，ρ)→0(k→∞).因此，必存在迭代序列{ak}的一个收敛子列{akj}和一个点a*∈Rn，当j→∞时，满足akj→a*.又因为{ak}是有界的，从而，当k→∞时，ak→a*.

结论证毕.

当φ=δk时，由定理3.3可得到以下结论.

推论3.2[9]已知映射 A∶Rn→Rn的单调映射，并且映射A是关于Lipschitz常数ξ＞0的Lipschitz连续映射，序列{ak}是算法3.2中定义的迭代序列，如果常数ρ＞(+1)ξ，那么，迭代序列{ak}收敛于问题(2)的一个解a*∈Rn.

4 结语

本文针对文献[9]中的非线性混合隐变分不等式问题，主要用一种新的Mann迭代算法求解一类非线性混合隐变分不等式的解，并证明其解的收敛性.更进一步推广了文献[9]中的结论.

[1] BAIOCCHI C，CAOPELO A.Variational and quasivariational inequalitises，application to fred boundary problem[M].New York:Willey，1984.

[2] GIANNESSI F，MAUGERI A.Variational inequalities and network equlibrium problems，plemum[M].New York:[s.n.]，1995.

[3] GLOWINSKI R，LIONS J L，TREMOLIERES R.Numerical analysis of variational inequalities[M].Amsterdam:North－Holland，1981.

[4] HARKER P T，PANG J S.Finite－dimensional variational inequality and nonlinear complementarity problems:a survey of theory，algorithms and applications[J].Mathematical Programming，1990，48:161 －220.

[5] HE B S.A class of projection and contraction methods for monotone variational inequalities[J].Applied Mathematics and Optimization，1997，35:69－76.

[6] HUANG N J.A new method for a class of nonlinear set－ valued variational inequalities[J].Journal of Applied Mathematics and Mechanics，1998，78:427 －430.

[7] YUAN，GEORGR X Z.KKM theory and applications in nonlinear analysis[M].New York:Marcel Dekker，1999.

[8] BREZIS H.Opereateurs maximaux monotone et semigroups de contractions dans－ les espaces de Hillbert[M].Amsterdam:North－Holland，1973.

[9] HUANG N J，FANG Y P.A new iterative algorithm for a class of nonlinear mixed implicit variational inequalities[J].Applied Mathematics Letters，2003，16:507 －511.