关于Orlicz空间中p一致凸性的刻画

许立滨，鄂明川，于继杰

(1.哈尔滨理工大学应用科学学院哈尔滨150080;2.哈尔滨电力职业技术学校哈尔滨150030)

1 引言

自1932年著名波兰数学家W·Orlicz引入Orlicz空间以来，Orlicz空间理论因其重要的理论性质和应用价值得到了长足的发展.关于赋Orlicz范数和Luxemburg范数的Orlicz空间的几何性质研究的已近乎完善，而赋p－Amemiya范数Orlicz空间几何性质的研究刚刚开始.p一致凸性是Banach空间重要的几何性质，本文将分别对赋 p－Amemiya范数、Luxemburg范数及Orlicz范数的Orlicz空间的p一致凸性做系统的的研究.

下面先给出一些基本概念:

设X是实Banach空间，B(X)和S(X)分别表示空间的单位球和单位球面.

映射Φ:R→[0，∞]被称为Orlicz函数是指Φ是偶，凸，在R+上连续，仅在零点等于零的函数，并令p(u)是Φ(u)的右导数.对每个Orlicz函数Φ，定义它的余函数 Φ:R→[0，∞]，

Ψ(v)=sup{u|v|－Φ(u)∶u≥0}易知余函数Ψ也是Orlicz函数.

设(G，∑，μ)是 δ－有限的测度空间，μ 是非原子且完备的测度，Lo(μ)表示所有定义在集合G上的可测函数的全体，对一给定的Orlicz函数Φ，在Lo(μ)上定义凸泛函

IΦ(x)= ∫GΦ(x(t))dμ

由Orlicz函数Φ所生成的Orlicz空间LΦ:

LΦ={x∈Lo(μ)∶IΦ(cx) ＜ ∞，存在某个c ＞0}及Orlicz空间LΦ的子空间:

EΦ={x∈Lo(μ)∶IΦ(cx) ＜ ∞，对任意c＞ 0}

且满足

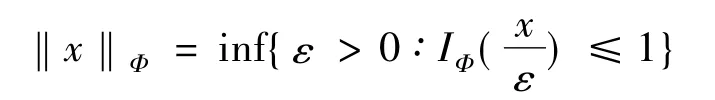
或等价的Orlicz范数:

在 Orlicz空间中，Orlicz范数与如下的Amemiya范数是等价的[1]

LΦ通常赋以如下的Luxemburg范数:

为简化记号，令

k ∈ K(x)[1]，对 t ＞ 0，令

p－(t)=sup{p(s)∶0≤s＜ t}，且p－(0)=0.

称Orlicz函数Φ满足Δ2－条件(简记为Φ∈Δ2)是指若存在正整数K和u0＞0，使得对于|u|≥ u0，有 Φ(2u) ≤KΦ(u).

称Orlicz函数满足 ▽2－条件(简记为 Φ ∈▽2)是指它的余函数Ψ满足Δ2－条件.

记SΦ为Φ的所有严格凸点构成的集合，即若u，v∈ R，α ∈ (0，1)，且

αu+(1 － α)v∈ SΦ，则

Φ(αu+(1－α)v) ＜ αΦ(u)+(1－α)Φ(v).

在LΦ中引入如下泛函:

2 主要结果

引理 2.1[2]∀x ∈ LΦ，‖x‖L= ‖x‖Φ，∞≤ ‖x‖Φ，p≤ ‖x‖Φ，1=‖x‖Φ.

引理2.2[1]对一切 x∈ LΦ有

‖x‖L≤ ‖x‖Φ≤ 2‖x‖L.

引理2.3[1]若 Φ(u) ∈ Δ2，则 ∀ε1＞ 0，

∃δ1＞ 0，使得

‖u‖L≥ ε1⇒ρΦ(u) ≥ δ1

定理 2.1 对一切 x∈ LΦ有 ‖x‖L≤‖x‖Φ，p≤ 2‖x‖L.

证明 利用引理2.1和引理2.2可以推出此结论.

定理2.2 若Φ(u)∈Δ2，则∀ε ＞0，∃δ＞0，使得

‖u‖Φ≥ε⇒ρΦ(u)≥δ

证明 若对∀ε＞0，有‖u‖Φ≥ε，利用引理2.2可以推出

因此，利用引理2.3可以推出:

∃δ＞ 0 s.t.ρΦ(u) ≥ δ

定理2.3 若Φ(u)∈Δ2，则∀ε ＞0，∃δ＞0，使得

‖u‖Φ，p≥ ε⇒ρΦ(u) ≥ δ

证明 若对∀ε＞0，有‖u‖Φ，p≥ε，利用定理2.1可以推出:

因此，利用引理2.3得出:∃δ＞ 0，使得ρΦ(u)≥δ.

定理2.4 设 Φ 是 N 函数，Φ(u)∈ Δ2，令M(u)=Φp(u)，(p≥2).若Φ(u)是一致凸的，则赋Luxemburg范数的 Orlicz空间(LM，‖·‖L)是p一致凸的.

证明 由于Φ是N函数，所以由N函数的定义可知:M也是 N函数.赋 Luxemburg范数的Orlicz空间(LM，‖·‖L)是p一致凸的当且仅当对任意的u，v∈S(LM)，存在c＞0，使得对给定0≤ h≤1，有

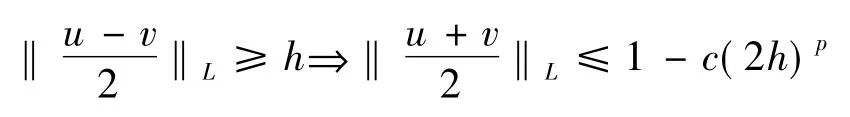
由于Φ(u)∈Δ2，即∃K ＞2和u0≥0使得Φ(2u)≤KΦ(u)，(u≥u0).则M(2u)= Φp(2u)≤ KpΦp(u)=KpM(u)，即 M(u) ∈ Δ2.因此利用引理2.3可知:要证本定理，只须证

对于上述h，选取u0＞0，使得M(u0)mesG ＜(h－hp)/2，并令

ε'=((h－hp)/2)1/p.由于Φ(u)是一致凸的，即对上述的 u0，ε'，∃δ＞ 0，当

|u － v|≥ ε'max(|u|，|v|)≥ ε'u0时，有

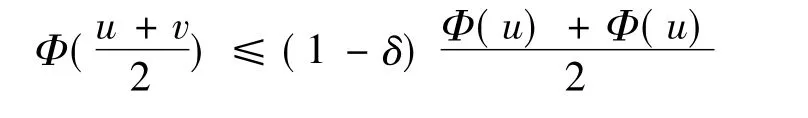
因此

又由于p≥2，

即M(u)也是一致凸的.

因ε'＜1，由G2的定义及

α，β∈ R，有

于是

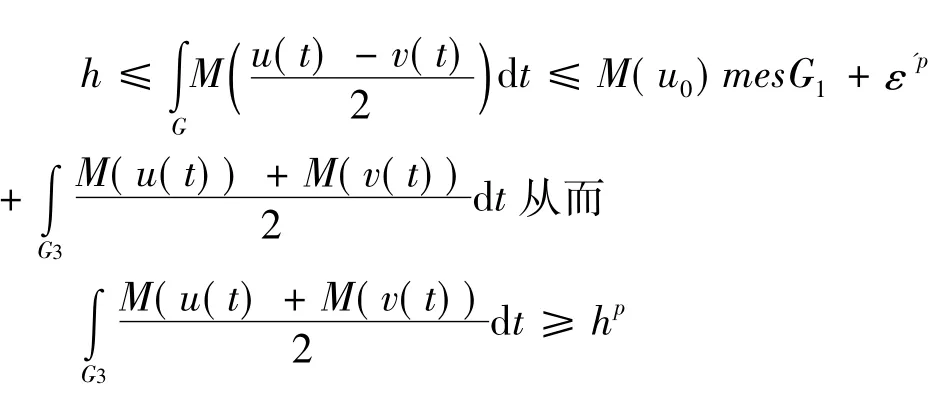
由于M在G1，G2上是凸函数，在G3上是严格凸函数，因此有

令 δ=c2p，即

定理2.5 设Φ是N函数，Φ(u)∈Δ2，令M(u)=Φp(u)，(p≥2).若Φ(u)是一致凸的，则赋Orlicz范数的Orlicz空间(MM，‖·‖M)是p一致凸的.

证明 由于Φ是N函数，所以由函数的定义可知:M(u)也是N函数.赋Orlicz范数的Orlicz空间(LM，‖·‖M)是p一致凸的当且仅当对任意的u，v∈S(LM)存在c＞0，使得对给定0≤h≤1，有

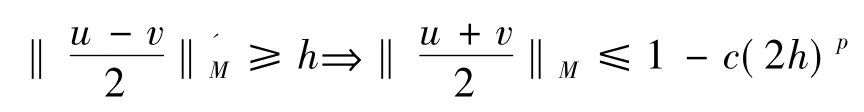
由于Φ(u)∈Δ2，即∃K ＞2和u0≥0使得Φ(2u) ≤ KΦ(u)，u(≥ u0).则

M(2u)= Φp(2u)≤KpΦp(u)=KpM(u)，即M(u)∈Δ2.因此利用定理2.2可知:要证本定理，只须证

证明过程与定理2.4的证明过程类似.

定理2.6 设 Φ 是 N 函数，Φ(u)∈ Δ2，令M(u)= Φp(u)，(p≥2).若Φ(u)是一致凸的，则赋p－Amemiya范数的Orlicz空间(LM，‖·‖M，p)是p一致凸的.

证明 由于Φ是N函数，所以N由函数的定义可知:M(u)也是N函数.赋p－Amemiya范数的Orlicz空间(LM，‖·‖M，p)是p一致凸的当且仅当对任意的u，v∈S(LM)，存在c＞0，使得对给定0≤ h≤1，有

由于Φ(u)∈Δ2，即∃K ＞2和u0≥0使得Φ(2u)≤KΦ(u)，(u≥u0).则M(2u)= Φp(2u)≤ KpΦp(u)=KpM(u)，即 M(u) ∈ Δ2.因此利用定理2.3可知:要证本定理，只须证

证明过程与定理2.4的证明过程类似.

本文分别给出了赋 p－Amemiya范数、Luxemburg范数及Orlicz范数的Orlicz空间具有p一致凸性的充分条件，但对于必要条件还需更深入地研究.

[1] CHEN S T.Geometry of Orlicz spaces[M].Dissert.Math，1996，356:1 －204.

[2] CUI Y，DUAN L，HUDZIK H.Basic theory of p － Amemiya norm in Orlicz spaces:extreme points and rotundity in Orlicz space sequippedwith thesenorms[J]，NonlinearAnal.，2008，69:1796 －1816.

[3] CUI Y，HUDZIK H，PLUCIENNIK R.Extreme points and strongly extreme points in Orlicz spaces equipped with the Orlicz norm[J].Z.Anal.Anwendungen，2003，22:789－817.

[4] CHEN L L，CUI Y，HUDZIK H.Criteria for complex strongly extreme pointsofMusielak Orlicz function spaces[J].Nonlinear Anal.，2009，70:2270 － 2276.

[5] HUDZIK H， NARLOCH A. Relationships between monotonicity and complex rotunditypropertieswith some consequences[J].Math.Scand.，2005，96:289 － 306.

[6] CHEN L L，CUI Y N.Complex extreme points and complex rotundity in Orlicz function spaces equipped with the p－Amemiya norm[J]，Nonlinear Analysis，2010，73(5):1389－1393.

[7] CUI Y N，HUDZIK H，LI J J.Strongly extreme points in Orlicz space equippedwith the p － Amemiya norm[J].Nonlinear Analysis，2009，71(12):6343 －6364.

[8] 刘培德.鞅与Banach空间几何学[M].武汉:武汉大学出版社，2007:179－215.

[9] 段丽芬，崔云安.广义Orlicz范数和广义Luxemburg范数[J].兰州理工大学学报，2006，32(2):131－134.

[10] 段丽芬，崔云安.广义Orlicz范数的Orlicz空间强端点[J].浙江大学学报，2009，36(1):6－11.

[11] 李小彦，崔云安.特殊Orlicz函数空间的光滑点[J].哈尔滨商业大学学报:自然科学版，2010，26(4):439－441.