品味定性分析在物理解题中的妙用＊——一道选择压轴题的定性与定量求解

季正华

（常州市北郊高级中学 江苏 常州 213031）

高考物理在考查知识的同时，注重考查能力，其中包括（定性与定量）分析综合能力和应用数学处理物理问题的能力.上海市宝山区2013届高三第一学期期末调研与江苏省扬州中学2013届高三第二学期质量检测卷选择题的压轴题则提供了很好的示范.在这里和大家一起赏析这道压轴题.

【题目】如图1所示，在光滑的水平地面上有一个表面光滑的立方体，质量为M.一长为L的轻杆与水平地面成α角，轻杆的下端用光滑铰链连接于O点，O点固定于地面上.轻杆的上端连接着一个质量为m的小球，小球靠在立方体左侧.立方体右侧受到水平向左推力F的作用，整个装置处于静止状态.若现在撤去水平推力F，则下列说法中正确的是

A.在小球和立方体分离前，若轻杆与水平地面成β角，小球的速度大小为v1，立方体的速度大小为v2，则有v1＝v2sinβ

B.小球在落地的瞬间和立方体分离

C.和立方体分离时小球只受重力

D.和立方体分离前小球的机械能不守恒

图1

答案：选项C，D.

解析：考虑小球和立方体分离前的速度大小的关系，可将小球做圆周运动的线速度v1分解为水平分量vx和竖直分量vy，如图2所示.

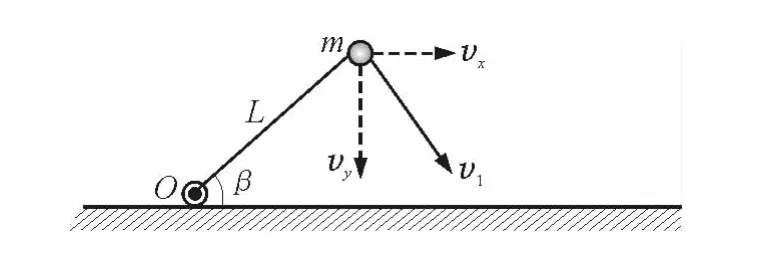
图2

由题可知，水平分量vx与立方体的速度v2大小相等，即v2＝v1sinβ，选项A错误.也可以根据相对运动速度关系v1相对2＝v1－v2求解.小球和立方体分离前相对于立方体的速度沿着立方体左侧竖直向下，如图3所示.

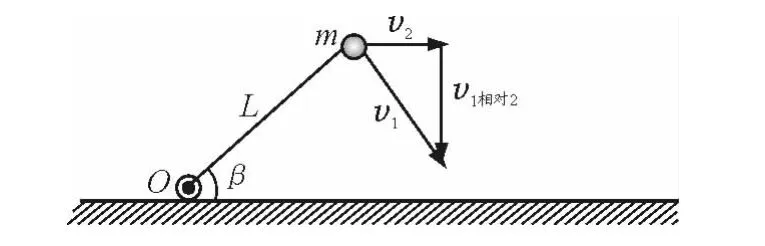
图3

由矢量运算可得

根据机械能守恒的条件，易得选项D正确.对于选项B，C，可以尝试考虑从定量和定性两种方法来处理.

方法1：定量分析法

利用机械能守恒、运动的合成与分解和圆周运动知识，定量分析.由机械能守恒得

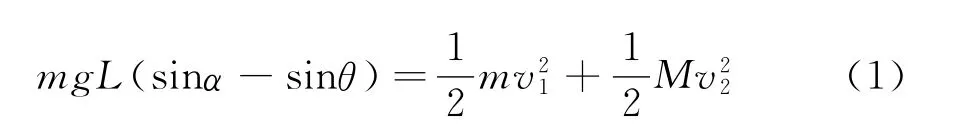
其中θ为轻杆与水平地面的夹角.由运动的合成与分解得

由式（1）、（2）可解得

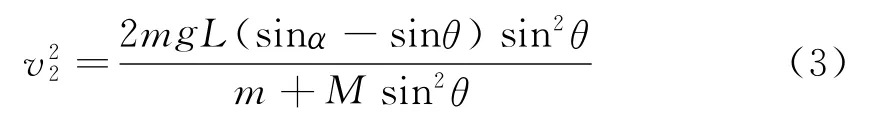
分离时，立方体的速度必定达到最大值（小球的水平速度分量也达到最大），之后小球的水平速度分量将小于立方体的速度，令

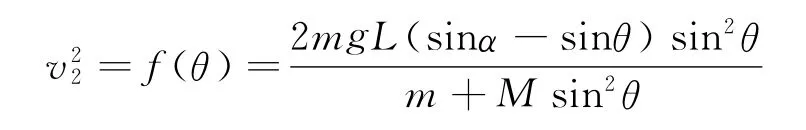
求解分离时θ满足

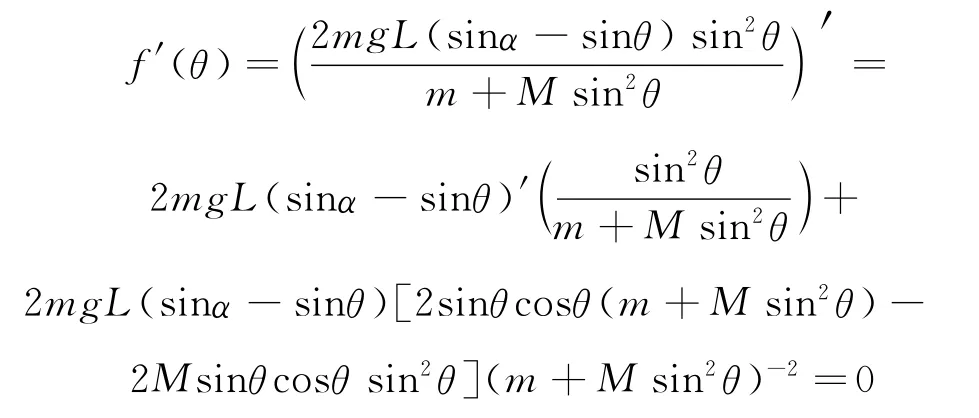
化简上式得

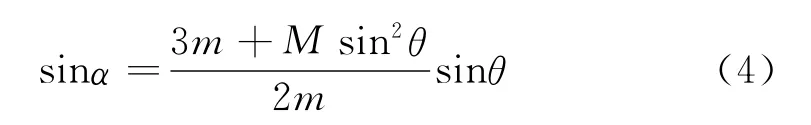
分离时，小球受到的向心力为

由式（1）、（2）、（5）得

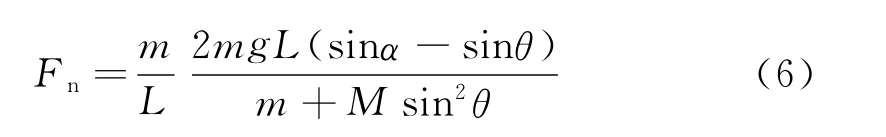
将式（4）代入式（6）得

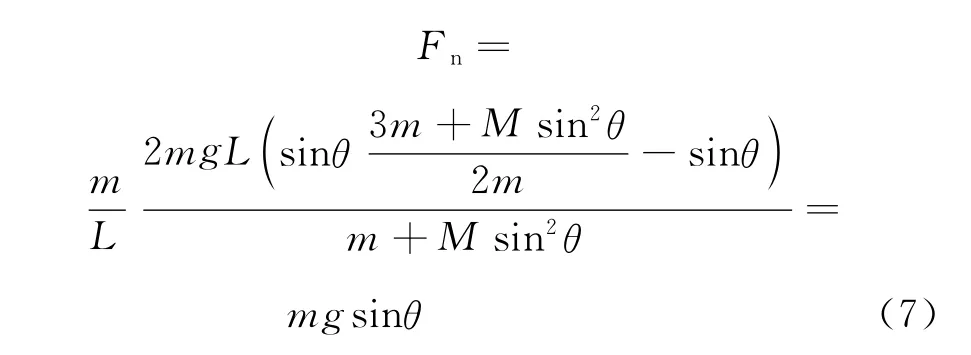
式（7）说明，在分离瞬间，铰链杆对小球没有作用力，重力沿杆方向的分力提供向心力，选项C正确得证.

方法2：定性分析法

利用两物体分离临界条件（从力学观点看，N＝0；从运动学观点看，分离瞬间两物体的速度和加速度仍相等）作定性分析.对于选项B，若小球在落地的瞬间和立方体分离，此时小球的水平速度分量为零，而立方体的速度大小一定不为零，与分离的临界条件矛盾，所以选项B错误.对于选项C，小球和立方体分离临界的加速度满足小球加速度的水平分量与立方体的加速度相同，即a1x＝a2（见下文证明）.而此时立方体水平方向受力为零，则

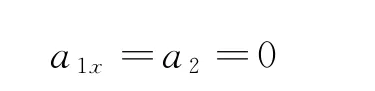
又因为轻杆对小球的作用力只能沿杆方向，所以，小球与立方体分离时不受杆的作用力，只受重力.选项C正确.

证明：设小球与立方体分离时的加速度为a2，由式（2）得

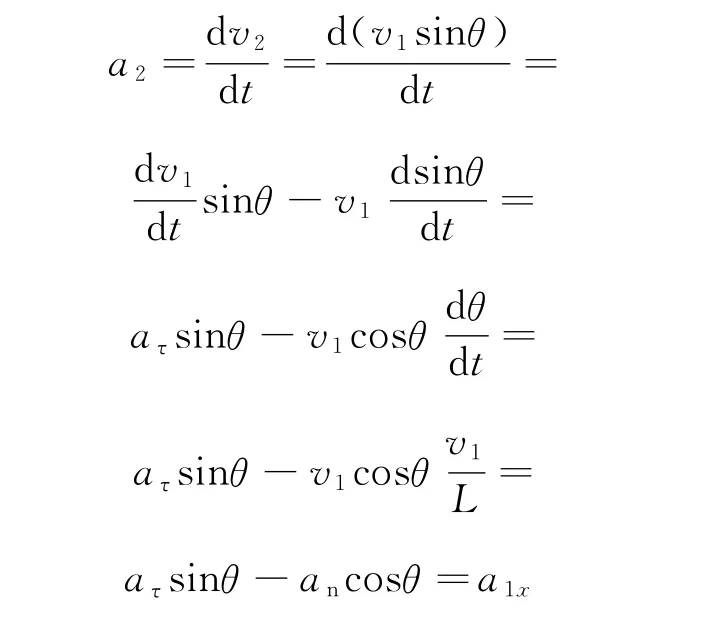
如图4所示.

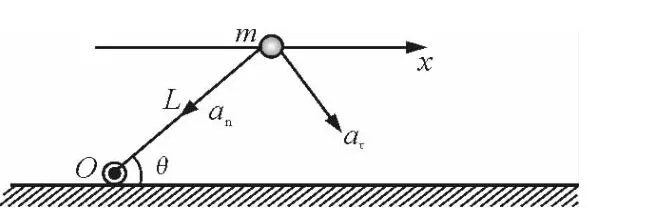
图4

分析与点评：本题的错误率较高，考查了学生对运动的合成与分解、机械能守恒以及力与运动的关系等知识的掌握，同时也考查了学生综合分析和解决问题的能力.本题求解从定量与定性角度作了分析，定量求解对学生应用数学处理物理问题的能力要求较高，而定性分析只需抓住分离瞬间的动力学与运动学条件这一关键进行逻辑推理，问题便可迎刃而解.

纵观近年高考，特别是执行新课程标准的省市，要求考生注意领会物理研究方法，相应的运用定性判断方法求解的题目逐年增多，因此，加强定性分析能力的培养和训练，是中学物理教学中需要重视的问题.