多体卫星MIMO控制及稳定裕度研究

李信栋 苟兴宇

北京控制工程研究所，北京 100190



多体卫星MIMO控制及稳定裕度研究

李信栋 苟兴宇

北京控制工程研究所，北京 100190

针对两输入两输出的多体卫星系统模型，采用并矢展开设计法这一多变量频域设计技术，实现卫星本体俯仰姿态和附件指向的多输入多输出(MIMO)控制，利用Nyquist稳定判据证明系统的稳定性；在此基础上讨论卫星本体姿态控制与附件指向控制带宽的关系，然后利用回差阵奇异值法计算MIMO控制系统的稳定裕度，并分析稳定裕度计算结果的保守性，数值仿真验证了算法的有效性以及稳定裕度分析结果的正确性。 关键词 多体卫星；并矢展开设计法；回差阵奇异值；稳定裕度； 卫星控制

一般的多体卫星既要对星本体进行姿态控制，又要对各附件进行指向控制，2种控制回路之间存在运动学和动力学耦合，这是一类典型的MIMO系统控制问题。此外，线性定常SISO系统有明确的稳定裕度计算方法，对某些特定的MIMO系统控制方法也有明确的稳定裕度结果，基于LQG的多变量控制系统具有至少60°的相角裕度和无穷大的增益裕度[1-2]；许多学者将奇异值分解方法应用到求解MIMO线性系统稳定裕度的理论研究中，并提出一种回差阵奇异值法[3]来计算系统的增益和相位裕度；然而对于一般MIMO系统的稳定裕度仍没有公认统一的定义[4]。在实际工程中，获得控制系统的稳定裕度可有助于航天器的安全在轨运行，寻求有效的计算方法得到明确的稳定裕度结果具有显著的工程意义，文献[5]仅完成了卫星天线指向复合控制的实物仿真验证，取得了有用仿真成果。然而国内目前还没有对多体卫星稳定裕度的系统研究。

为此本文对多体卫星MIMO控制系统的稳定裕度进行了探讨。文中研究两输入两输出多体卫星控制系统，系统模型简化地只考虑俯仰平面；并假设附件指向角做小角度机动。针对此系统的控制问题，结合系统模型本身的特性，采用多变量频域理论中的并矢展开设计方法，设计卫星本体姿态和附件指向控制的MIMO控制系统；并对卫星姿态及附件指向的控制带宽问题进行了讨论。用古典控制理论的Nyquist稳定性判据判断系统的稳定性，在此基础上，为满足实际工程要求，利用回差阵奇异值法计算出整个系统的稳定裕度，并讨论所得稳定裕度结果的保守性。

1 系统动力学建模

图1 平台+天线的两刚体构型

定义天线绕x轴和y轴的转动角分别为α和β，运用Newton-Eular法，以1x-2y转序为例，利用各坐标系之间的关系导出标量动力学方程。在平台姿态可以线性化、平台与附件机动角速度均不大的前提下，进一步将控制对象简化为俯仰平面问题，相应标量格式的动力学方程为[6-7]

(1)

式中，Ia,yy和Ib,yy分别为航天器平台与天线绕各自俯仰轴的转动惯量，xra,cc,cs为系统几何参数所决定的常系数，ma为天线质量，θ为平台姿态转角，β为天线转角，Mcy为绕航天器y轴的俯仰姿态控制力矩，Mβ为β转角控制力矩。

2 并矢展开设计方法及稳定性分析

英国学者Owens首先提出了并矢展开设计法，该方法可对控制对象由并矢传递函数矩阵描述的多变量系统进行有效的设计[8]。主要特点是系统传递函数满足一定的特性，即要求控制对象G(s)可分解为

(2)

式中L,R是m×m常数可逆矩阵，g1(s),g2(s),…，gm(s)是一组标量传递函数。可设计如下控制器

K(s)=R-1diag{k1(s),k2(s),…,km(s)}L-1

(3)

通过调整ki(s)使系统具有良好的整体性，计算系统闭环传递函数矩阵，来检验系统的瞬态响应、关联性及稳态误差是否符合设计要求。

2.1 控制器设计

假设天线指向角在俯仰平面内做小角度机动，即在β=0°附近线性化处理，则动力学方程为

(4)

(5)

其中

将控制对象G(s)由并矢传递函数矩阵分解得

(6)

其中LR=M-1。根据性能要求，设计控制器

K(s)=R-1diag{k1(s),k2(s)}L-1=

(7)

则系统开环传递函数矩阵为

(8)

闭环传递函数矩阵为

(9)

作2个标量系统g1(s)k1(s)和g2(s)k2(s)的对数幅频特性曲线，如图2所示。显然，2个标量系统在整个频带上具有比较一致的对数幅频特性，故系统一定是弱关联的。

图2 g1(s)k1(s)和g2(s)k2(s)的对数幅频特性

基于本文中的设计方法，通过图2的比较可看出星本体控制带宽与天线控制带宽大小相当；而对一般带有天线等附件的多体卫星，由于其附件跟踪目标的轨迹通常是在平台轨道坐标系中描述的，如果附件跟踪指向的精度要求与姿态控制精度接近、甚至更高，则附件机动的最终指令一般需要引入星本体姿态的修正，因此，一般来说星本体-附件同时机动控制器的设计原则为：附件指向控制的带宽必须大于星本体姿态机动控制的带宽[5]。通过分析认为本文之所以出现二者带宽相当，这是因为采用并矢展开法设计的结果，此结果一般适用于天线跟踪指向精度远低于卫星姿态控制精度，从而不需要引入从卫星姿态到天线指向的运动学前馈的情形。

2.2 稳定性分析

对于采用并矢展开法进行设计的控制系统，可通过Nyquist理论来判别整个闭环系统稳定性，并且有稳定性判据如下：

定理1 由方程

H(s)=[Im+G(s)K(s)]-1G(s)K(s)

(10)

描述的多变量反馈系统为渐近稳定的充分必要条件是[9]

(11)

对于多变量系统其回差阵满足关系式

(12)

其中φc(s)为闭环系统特征多项式,φ0(s)为开环系统特征多项式。由方程(8)和(12)，可得开环系统特征多项式φ0(s)为

φ0(s)=s4(s+3.7)(s+5)

(13)

可看出φ0(s)没有位于s右半平面零点，故n0=0。作gi(s)ki(s)(1≤i≤2)的Nyquist图,如图3所示。

图3 g1(s)k1(s)和g2(s)k2(s)的Nyquist曲线

3 稳定裕度分析

对于MIMO线性系统，稳定裕度的计算不像SISO系统那样简单，这里要考虑到各回路间的耦合问题。许多学者研究表明可采用回差阵奇异值法计算MIMO系统的稳定裕度，即利用系统回差阵的最小奇异值来表示系统的相对稳定性[3]。对一般如图4所示系统模型，其中G(s)∈Cn×n为系统标称模型，在输入端引入不确定性量测阵，令s=jω，则有

P(jω)=diag{kie(jφi)},i=1,2,…,n

(14)

我们希望得到所有回路中ki和φi同时变化且变化多大时系统仍能保持稳定，也即ki和φi是系统的相对稳定性的度量值。

图4 系统模型

I+GP=[(P-1-I)(I+G)-1+I](I+G)P

(15)

(16)

若考虑增益和相位在每个通道同时变化的情况，采用方程(14)，受摄动系统稳定的充分条件变为

(17)

GM=-20lg(1-m),PM=2arcsin(m/2)

(18)

本文中的系统模型是简化后的两输入两输出线性模型，可计算其回差阵[I+G(s)K(s)]的表达式为：

I+G(s)K(s)=

(19)

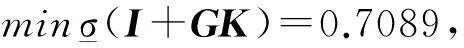
分析上述结果可知，并矢展开法设计的控制器使系统具有比较满意的稳定裕度，可以看出回差阵奇异值计算方法简单且计算量较小；并且有效地解决了MIMO控制系统稳定裕度计算时各回路之间的耦合问题，重要的是该方法给出了闭环系统保持稳定所容许的所有回路的幅值或相位同时变化程度。但是也应该看到该方法具有一定的保守性，下面将作进一步的讨论。

4 仿真结果

针对卫星本体俯仰轴姿态运动和天线指向角运动同时跟踪情况下的MIMO控制系统进行仿真分析，绘制仿真图像，以验证上文所设计的控制器的有效性。

在本文中，对象模型参数取Ia,yy=0.438kg·m2,Ib,yy=3453kg·m2,ma=8kg,cc=-1.94m，cs=-0.22m，xra=-0.0056m，则动力学方程为：

可设计控制器为：

(20)

仿真中采用式(20)所示的控制器，令初始时刻各状态量的初始值θ0=0°,β0=0.1°。设计卫星本体俯仰轴姿态期望跟踪曲线和卫星天线指向角期望跟踪曲线分别为

在考虑有外部干扰力矩作用在星本体的情况下，研究卫星本体俯仰轴姿态运动和天线指向角运动同时跟踪期望轨迹时的系统控制能力。在式(1)所示的系统模型中，在第一个表达式中加入扰动项Tv=0.1πsin(πt/10)/180+0.0001 (N·m)，得到仿真结果如图5～8所示。

图5 星本体俯仰姿态期望轨迹及实际响应曲线

图6 卫星天线指向角跟踪轨迹及实际响应曲线

图7 星本体俯仰姿态和天线指向角的跟踪误差曲线

图8 星本体姿态控制力矩Mcy和天线驱动力矩Mβ

通过仿真结果可以看出，在加入外部干扰力矩情况下，俯仰姿态和天线指向角能快速跟踪期望轨迹，两者跟踪误差最终都趋于较小值；这说明所采用的控制方法对平台-附件控制对象模型具有良好的解耦控制能力，同时能保证较高的天线跟踪指向精度和姿态控制精度，因此所设计控制方法使系统具有较好的跟踪效果，且具有一定的鲁棒性，仿真结果满足设计要求。

进一步地，对采用回差阵奇异值法计算得到的稳定裕度结果进行分析。根据上面回差阵奇异值法求得的系统稳定裕度，当系统两通道同时滞后41.52°的相位角时，可得系统的跟踪误差曲线如图9所示；从图中可看出，响应初始阶段系统振荡现象明显，但是系统仍然稳定并没有达到临界稳定状态。若进一步增大两通道的滞后相角，滞后相角取到53.19°时，得到系统的响应曲线如图10所示，从图中可看出，系统出现发散趋势，即将变得不稳定。

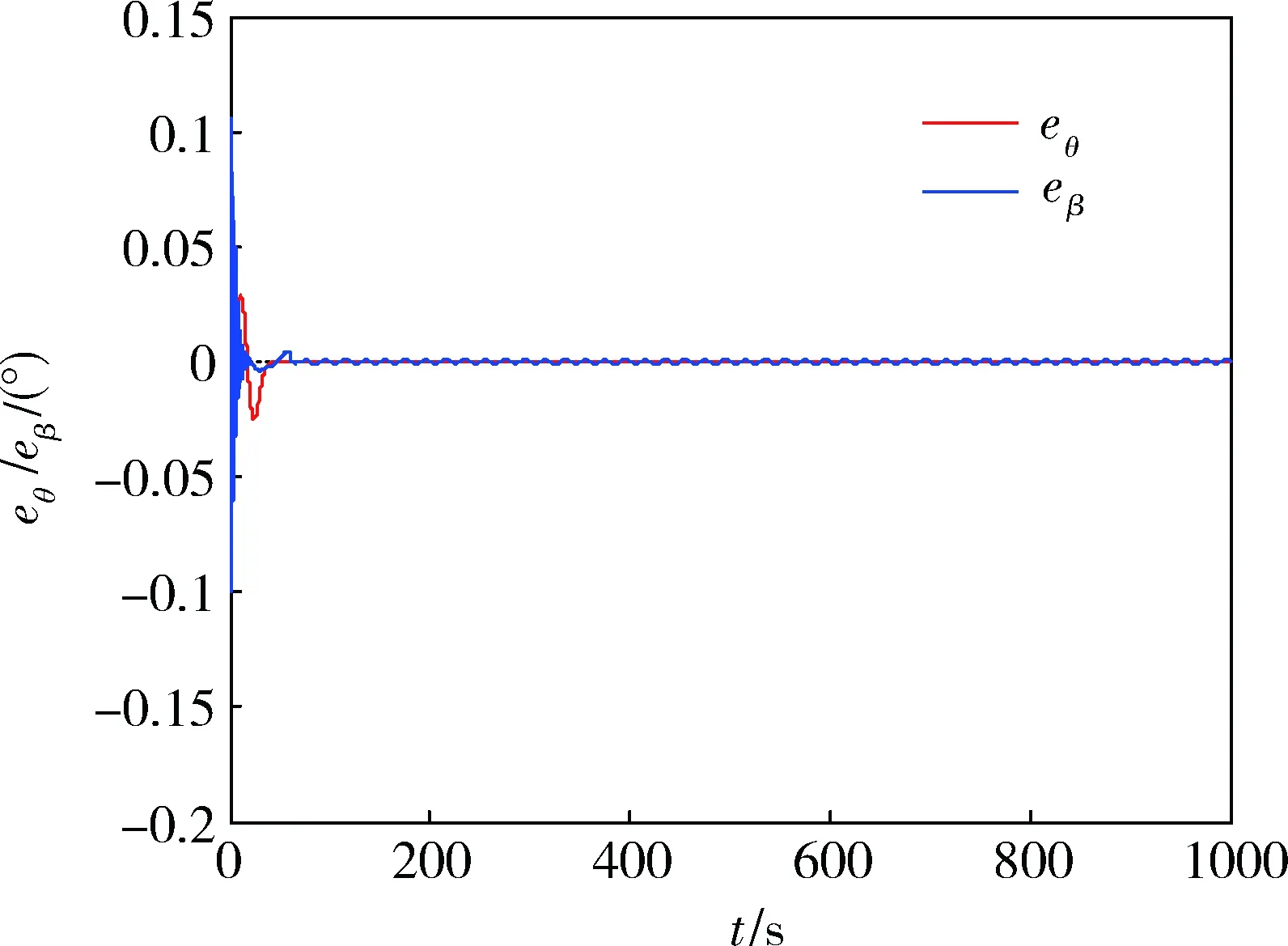
图9 系统滞后41.52°相角时跟踪误差曲线

图10 系统滞后53.19°相角时输出响应曲线

分析上述情形可看出采用回差阵奇异值法求得的系统稳定裕度的结果是偏保守的，该方法没有准确地给出系统由稳定状态达到临界稳定状态时所容许的相角能变化的最大范围。研究认为有以下原因：

1)回差阵奇异值法理论本身的不足，式(16)是受摄动系统稳定的充分条件而不是充要条件，除了式(16)所示条件外，还有别的条件仍能保证系统的稳定性，而这些条件的忽略可能造成对系统幅值和相位裕度的保守估计；

2)文中稳定裕度的计算是基于式(20)所示线性控制系统，而仿真中是针对非线性系统模型，这也可能造成稳定裕度大小的不一致。

5 结论

本文针对两输入两输出多体卫星模型，采用多变量频域技术中的并矢展开法设计卫星本体姿态和附件指向角的MIMO控制系统，仿真结果表明所设计的控制器有较强的鲁棒性，而且控制器结构较简单，易于工程实现。此外，文中所设计的天线控制带宽与星本体控制带宽相当，这是由于本文设计过程中没有考虑本体姿态对天线的前馈控制。最重要的一点，文中在保证稳定性的基础上，利用回差阵奇异值法得到了控制系统的稳定裕度，并讨论该方法出现保守性的原因。下一步工作要在系统控制中考虑天线的工程执行机构模型，同时改善稳定裕度计算方法的保守性，使系统的控制效果和稳定裕度的计算结果更具有工程参考价值。

[1] Safonov M G, Athans M. Gain and Phase Margin for Multiloop LQG Regulators[J]. IEEE Transactions on Automatic Control, April 1977, 22: 173-179.

[2] Lehtomaki N A, Sandell N R, JR, M Athans. Robustness Results in Linear-Quadratic Gaussian Based Multivariable Control Designs[J]. IEEE Transactions on Automatic Control, February 1981, 26(1): 75-92.

[3] Mukhopadhyay V, Newsom J R. Application of Matrix Singular Value Properties for Evaluating Gain and Phase Margins of Multiloop Systems[C]. AIAA Guidance Navigation and Control Conference, San Digeo, California. 1982, AIAA-82～1574．

[4] 瞿福存, 史忠科, 戴冠中. MIMO系统稳定裕度的几个定义[J]. 飞行力学, 2002, 20(2): 6-9. (Qu Fucun, Shi Zhongke, Dai Guanzhong. Stability Margin Definitions for MIMO Systems[J]. Flight Dynamics, 2002, 20(2): 6-9.)

[5] 李季苏, 曾海波, 李铁寿.多体卫星复合控制物理仿真试验系统[J]. 航天控制, 2003, 21(2) :27-32. (Li Jisu, Zeng Haibo, Li Tieshou. Physical Simulation Test System for Combined Control of Multi-body Satellite[J]. Aerospace Control , 2003, 21(2) :27-32.)

[6] 苟兴宇, 陈义庆, 李铁寿, 等.平台附件同时机动及其复合控制初探[J].空间控制技术与应用, 2009, 35(5): 1-5.(Gou Xingyu, Chen Yiqing, Li Tishou, etc. Introduction to Simultaneous Maneuvers and Composite Control of Spacecraft Platform and its Appendages[J]. Aerospace Control and Application, 2009, 35(5): 1-5.)

[7] 曾海波.挠性多体卫星指向控制设计研究[D].北京控制工程研究所, 2003.

[8] Owens D H. Feedback and Multivariable System[M].London, Peter peregrines, 1978.

[9] 白方周, 庞国仲, 等.多变量频域理论与设计技术[M].国防工业出版社, 1988.

On MIMO Control and Stability Margin of Multi-Body Satellite,China

LI Xindong GOU Xingyu

Beijing Institute of Control Engineering, Beijing 100190， China

Thepitchattitudeandantennapointingcontrolofmulti-bodysatellitesarepresentedinthispaper,thestabilitymarginofthemulti-inputmulti-output(MIMO)linearcontrolsystemisgiven.Firstly,thedyadicexpansionmethodisutilizedtodesignthecontrollerbasedonthetwo-inputtwo-outputsystemmodel,andastabilityanalysisoftheresultingclosed-loopsystemisincludedthroughtheNyquiststabilitycriterion.Therelationshipbetweenthesatelliteattitudecontrolbandwidthandtheantennapointingcontrolbandwidthisstudied.Secondly,thestabilitymarginoftheMIMOcontrolsystemisobtainedbycomputingtheminimumsingularvalueofthesystemreturndifferencematrix.Finallytheconservativenessofthestabilitymarginisdiscussed,andsimulationresultsarepresentedtoshowthatthisdesigntechniqueiseffectiveandtheanalysisisreasonable.

Multi-bodysatellites;Dyadicexpansionmethod;Minimumsingularvalueofthereturndifferencematrix;Stabilitymargin;Satellitecontrol

2012-09-10

李信栋(1986-), 男,山东人 ,博士研究生, 研究方向为航天器姿态控制; 苟兴宇(1970-), 男,四川人 , 研究员, 主要研究方向为航天器姿态、轨道动力学与控制。

V448.22

A

1006-3242(2013)05-0025-06