一种弹载多级容错组合导航系统设计*

雷浩然 陈 帅 程 晨

南京理工大学自动化学院，南京 210094



一种弹载多级容错组合导航系统设计*

雷浩然 陈 帅 程 晨

南京理工大学自动化学院，南京 210094

针对高动态下由于IMU,GPS异常导致松性组合导航系统精度下降,甚至无法正常工作的问题，具体分析了可能出现的多种异常组合，给出了相应的处理策略。在此基础上设计了一种基于DSP/FPGA硬件平台的弹载多级容错组合导航系统(MFTINS)，并将其应用于某新型导弹的组合导航。同时，为了解决高动态情况下常规卡尔曼滤波(CKF)收敛性不佳、滤波精度降低甚至发散的问题，提出自适应卡尔曼滤波(AKF)。通过试验和分析，验证了组合导航系统设计及AKF的适用性和有效性。 关键词 弹载；多级容错；组合导航；高动态；自适应；卡尔曼滤波

增大射程、提高制导精度、增强机动性、采用先进战斗部等已成为现代导弹的主要发展趋势[1]。某陆基新型导弹采用基于速度、位置的惯性/卫星组合制导将有效提高其主动段的制导精度，具有射程更远、体积更大、速度快等特点，有效提高了远距离打击能力和突防能力。

IMU和GPS接收机保持正常工作是导弹导航系统具有良好性能的前提，因此对IMU和GPS的性能提出了较高要求，同时要求组合导航系统具有较好的容错能力。此外，卡尔曼滤波作为惯性/卫星组合导航系统中的一项核心技术，其性能往往决定了导航系统的性能[2]。对于具有高动态、强振动、强机动等特性的载体而言，系统数学模型和噪声统计不准确、噪声突变等情况会造成常规卡尔曼滤波精度变差、滤波器稳定性下降，甚至导致滤波发散，极大地影响了组合导航系统的性能[3]。

本文以某导弹项目为背景，从提高SINS/GPS组合导航系统的可靠性、稳定性出发，以DSP/FPGA为硬件平台，设计了一种弹载多级容错组合导航系统，并采用自适应卡尔曼滤波算法，以提高导航定位的精度和系统性能。

1 系统硬件设计

本系统基于DSP/FPGA潜并行结构[4],实现多路实时通讯、数据采集、高速数据处理和实时输出的高性能嵌入式弹载计算机，主要模块包括：导航计算机模块、飞控计算机模块、舵机控制器模块。系统硬件总体结构如图1。

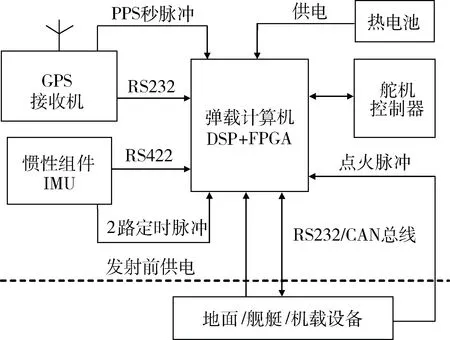
图1 硬件总体结构

DSP芯片采用TI公司的TMS320C6713B,它是一款32位高速浮点芯片，时钟最高频率为300MHz，峰值浮点运算能力可达1800MFLOPS,采用二级缓冲处理和256KB的额外匹配内存，具有丰富的外围模块。

系统采用光纤陀螺惯性测量单元，输出频率为200Hz；x,y,z三轴陀螺测量范围分别为±500°/s,±100°/s,±100°/s；x,y,z三轴加速度计测量范围分别为±50g,±15g,±15g；GPS接收机输出频率10Hz。

弹载计算机作为系统核心，其主要功能如下：

1)实现对弹上仪器的供配电；

2)通过RS232/422与GPS接收机、IMU通讯、接收数据并完成组合导航；

3)舵机控制及完成舵反馈数据采集；

4)通过RS232/CAN总线实现与测发控设备通讯，检测相关输入和输出开关量信号。

2 多级容错组合导航设计

当导弹运动具有高动态、强机动、大振动等特性时(如助飞爬升、机动飞行、弹箭分离等)，IMU和GPS工作状态即使出现极短的异常都可能降低组合导航精度，使系统稳定性变差，所以必须采取相应措施削弱不利影响，对于以惯导为主、GPS辅助定位的松组合导航系统尤为重要。为此，本文设计了一种多级容错的组合导航系统(MFTINS)，分为4个部分：数据解析模块、状态判别模块、决策匹配模块和导航输出模块。MFTINS主要流程如图2。

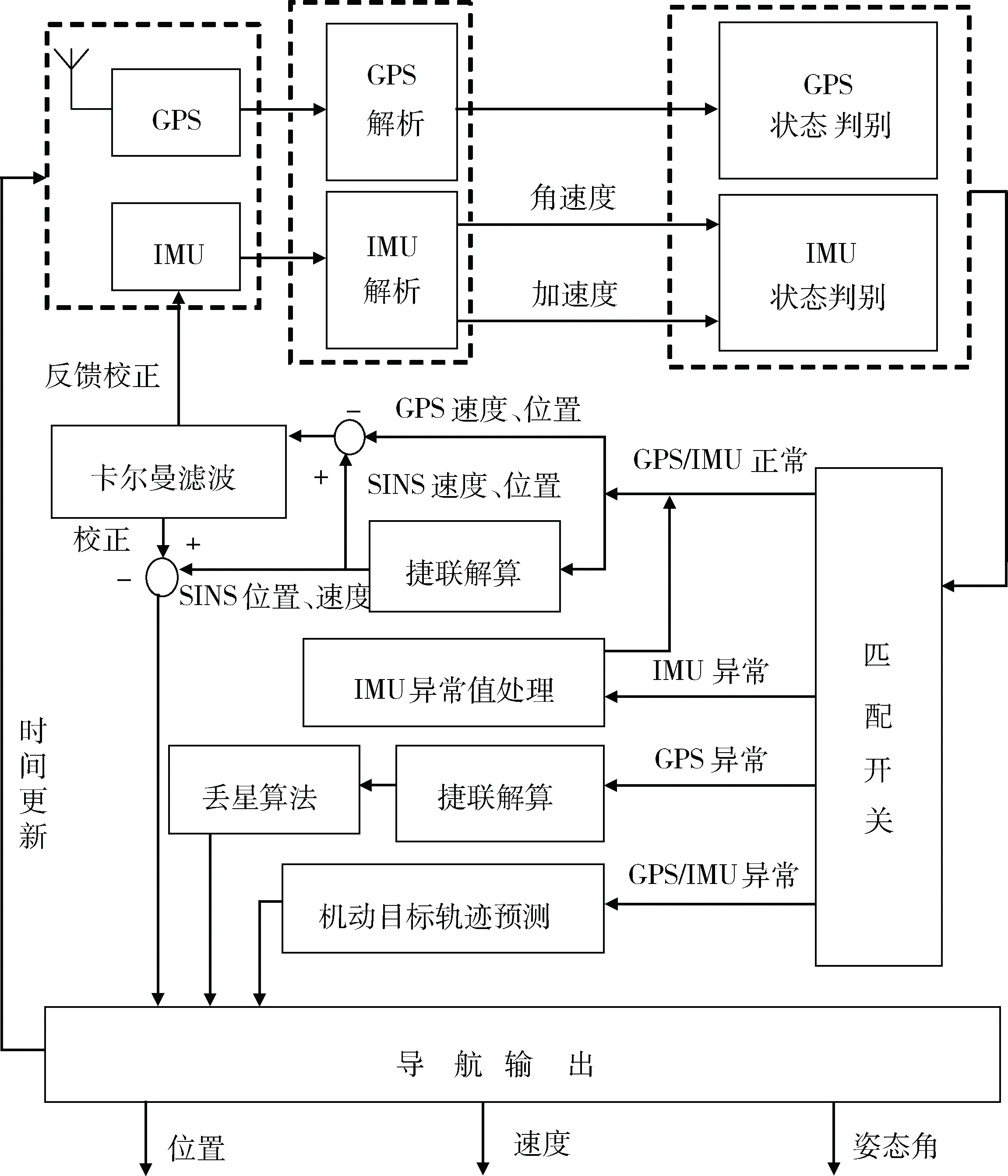
图2 MFTINS流程图

2.1 状态判别

正确判断惯性组件及GPS接收机的工作状态是决策匹配的前提，给出具体判别方法如下：

1)IMU异常判别。通常将惯组的动态极限作为阀值，如式(1)所示：

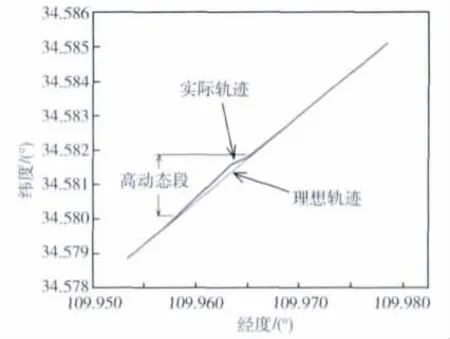
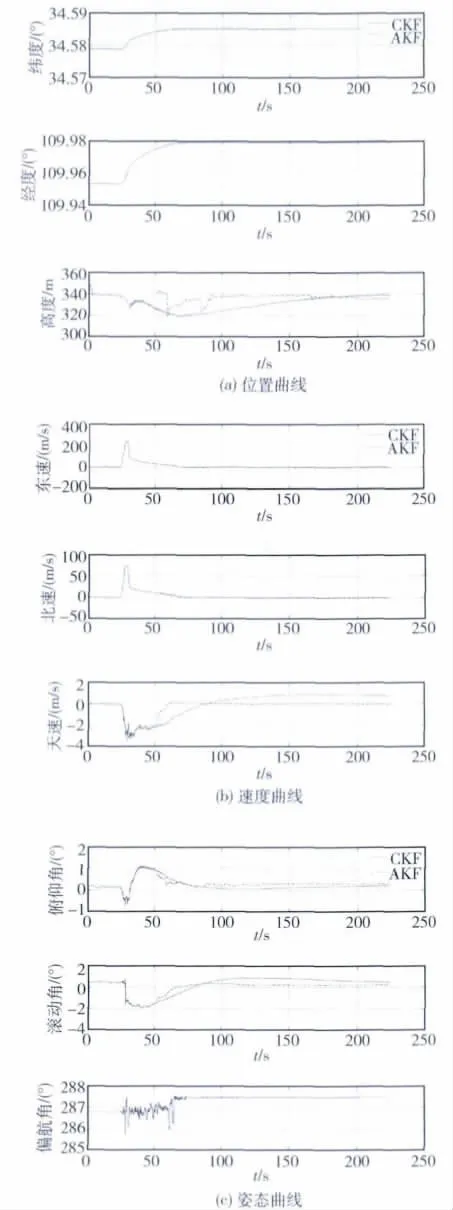
|Aaxis|

(1)

其中下标“axis”为加速度计、陀螺轴向标识，Amax和ωmax分别为加速度和角速度极限。当式(1)满足时，则认为IMU正常，否则IMU异常。

2)GPS异常判别。GPS工作状态采用内外2层判别。外层为收星条件判别，如式(2)所示:

Nsats≥n,xDOP≤dop

(2)

其中Nsats为收星数；n为设定最小收星数，通常设为4；xDOP为精度因子；dop为精度因子门限。当式(2)满足时，继续内层判别，否则认为GPS异常；内层主要依靠SINS在短时间内具有较好的稳定性和精度这一特性对GPS量测粗大误差进行判别,方法如式(3)和(4)所示：

|P(t)GPS-P(t)SINS|<δp

(3)

|V(t)GPS-V(t)SINS|<δv

(4)

其中P(t)GPS，V(t)GPS为GPS当前时刻量测位置和速度值,P(t)SINS，V(t)SINS为SINS解算位置和速度值，δP,δV为设定的位置和速度误差阀值。当式(3)和(4)满足时，则认为GPS正常，否则GPS异常。

2.2 决策匹配

决策匹配是整个MFTINS的核心部分，其根据GPS和IMU工作状态的不同匹配相应处理策略，以增强系统的适应性和鲁棒性，具体方法如下：

1)IMU和GPS均正常。采用松组合导航流程，即量测-解算-滤波-校正，其中滤波周期为1s；

2)IMU异常。放弃当前时刻获取的数据，采用前一时刻惯组量测值进行替代，如式(5)：

ω(k)axis=ω(k-1)axis,A(k)axis=A(k-1)axis

(5)

3)GPS异常。在GPS异常(如高动态下丢星失锁等)情况下，系统无法得到有效的GPS量测值输入，从而导致卡尔曼滤波器无法工作。在捷联解算后，采用照常进行状态及均方误差的时间更新，省略量测更新的方法处理短时间丢星情况[5],如式(6)～(8)所示,其中相关矩阵参见2.3节:

(6)

(7)

Pk=Pk,k-1

(8)

当量测缺失时间过长或者由此导致的状态估计均方误差过大时，应当否定滤波结果的有效性，甚至重置AKF。

当GPS从长时间异常恢复时，用GPS给出的位置、速度作为当前时刻组合导航的位置、速度值,同时惯性器件稳定性较好时，可采用误差状态转移阵估计出导航误差并进行修正[6]。首先在丢星期间计算与滤波周期相应的Фk,k-1并连乘，得到丢星前一时刻t0到当前时刻t1的状态转移矩阵,T为滤波周期,如式(9)所示：

Φt1,t0=Φt1,t1-T...Φt0+2T,t0+TΦt0+T,t0

(9)

然后由此及t0时刻的误差状态量推算出当前时刻的平台失准角误差ψt1，速度误差δVt1和位置误差δPt1，并修正导航输出，如式(10)所示：

(10)

4)IMU和GPS均异常。通常该情况较少出现，若高动态下出现此状况时，由于捷联解算及滤波均无法进行，如果仍采用前一时刻导航输出作为当前时刻结果或者甚至不采取任何措施，必将引入较大导航误差；当持续时间过长时，导航结果将严重偏离真实值。此时可采用针对机动目标的轨迹预测方法[7]，对载体当前时刻运动状态进行估计，削弱系统无法正常工作带来的不利影响。

2.3 滤波算法设计

2.3.1 系统状态与量测方程

系统时域状态与量测方程相关矩阵选取参见文献[8],对应的一阶离散化状态方程和量测方程如下：

Xk=Φk,k-1Xk-1+Γk-1Wk-1

(11)

Zk=HkXk+Vk

(12)

其中，Фk,k-1为tk-1时刻至tk时刻的状态转移矩阵；Гk-1为系统噪声驱动阵；Hk为测量关系阵；Vk为量测噪声向量；Wk-1为系统过程噪声向量，状态向量Xk如下:

Xk=[ψE,ψN,ψU,δVE,δVN,δVU,δL,δλ,δh,

εx,εy,εz,▽x,▽y,▽z]T

(13)

其中，前9个分量依次为平台失准角误差、速度误差和位置误差，后6个分量分别为陀螺漂移和加速度计零偏。

2.3.2 自适应卡尔曼滤波AKF

鉴于系统数学模型和噪声统计不准确、噪声突变等情况易造成常规卡尔曼滤波CKF滤波精度变差、滤波器稳定性下降，甚至出现滤波发散，MFTINS采用自适应滤波AKF，它是在CKF基础上引入基于新息的滤波发散判据并且加入自适应权重因子构成的，算法如式(6)、(7)及式(14)～(20)所示：

(14)

(15)

(16)

(17)

(18)

(19)

(20)

其中，式(14)为基于单步量测新息rk的滤波发散判据，λ为根据试验确定的常值系数，通常取1～5。文献[9]提出了基于滤波过程的滤波发散判定方法，然而其Pmin和Zmin即判定滤波稳定门限不易确定，较依赖于先验知识，不利于实时应用，故本文仍采用式(14)判据，若成立则滤波发散，反之则不发散。

在滤波发散情况下，由式(15)求出自适应权重因子Sk以扩大Pk,k-1的作用，增大滤波增益，从而增强新量测值的修正作用，进而抑制滤波发散[10-11]。

3 试验与分析

3.1 场地跑车试验

由于场地跑车试验用车的姿态尤其是航向角受人为驾驶因素影响较大，故该试验主要用于验证低动态下组合导航定位的位置重复性。

试验场地为体育场(路径闭合),通过监控平台存储6个定点的位置信息，并进行均方差统计。表1为位置均方差结果，图3为场地试验轨迹曲线，图4和5分别为场地试验轨迹曲线及位置曲线。

图3 试验设备示意图

表1 位置均方差

纬度范围(m)经度范围(m)高度范围(m)均方差0.971～3.03460.3564～1.40890.7256～1.005

图4 场地试验轨迹曲线

图5 场地试验位置曲线

从场地跑车试验结果看出，其位置重复性较好，表明该组合导航系统在低动态下具有良好的稳定性和较高的导航定位精度。

3.2 火箭撬试验

在场地跑车试验的基础上，通过火箭撬试验进一步验证组合导航系统在高动态下的性能。

试验初始偏航角为-73.2°，滚转角为0.378°，俯仰角为0.168°。由于受轨道约束，载体始末静止段姿态角大致保持一致。载体运动过程大致为：静止-加速-高动态运动-减速-静止，其总过程约224s,其中高动态运动段具有大加速度、大加加速度、大振动等特点，且存在GPS丢星失锁、惯组量测异常、噪声突变等复杂情况。

2组试验分别采用CKF和AKF，图6为火箭撬试验轨迹曲线，表2为CKF与AKF始末结果对比，图7(a)～(c)分别对应火箭撬试验位置、速度和姿态角曲线。

图6 火箭撬试验轨迹曲线

图7 火箭撬试验结果曲线

从试验结果看出，在高动态甚至恶劣情况下，CKF由于不具备发散在线判别、发散抑制措施以及缺乏噪声变化时的自适应能力等，其滤波效果和收敛性均较差，并且出现了滤波发散，导致滤波结果偏差过大，无法满足组合导航的要求。当使用AKF并采用MFTINS时，效果较好，无论滤波收敛性、滤波精度还是稳定性均优于CKF。

表2 CKF与AKF始末结果对比

4 结论

针对在高动态及多种复杂情况下CKF收敛差、滤波发散以及常规惯性/卫星松性组合导航系统性能不佳的问题，本文以DSP/FPGA为硬件平台，设计了一种弹载的多级容错组合导航系统(MFTINS)，以提高某新型导弹主动段的导航精度。通过场地跑车试验、火箭撬试验，验证了AKF的有效性和MFTINS的稳定性、可靠性及适用性，MFTINS也同样适用于其它采用松组合导航的导弹、载体。

[1] 林宗祥,孙永侃,熊正祥.国外反潜导弹系统综述[J].飞航导弹, 2011, 3: 50-54.

[2] 惠怀志,蔡伯根.组合导航信息融合算法的研究[J]. 北京交通大学学报, 2007, 31(2): 62-66. (HUI Huai-zhi,CAI Bai-gen. Algorithm of Information Fusion for an Integrated Navigation System[J]. Journal of Beijing Jiaotong University, 2007, 31(2): 62-66.)

[3] 张雨楠.INS/GPS组合导航系统滤波器设计[D]. 哈尔滨工程大学, 2007:48-52.

[4] 李宗涛.高动态捷联惯导系统的并行实现研究[D]. 浙江大学, 2011: 27-28.

[5] 谢钢.GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009: 131-132.(XIE Gang. Principles of GPS and Receiver Design[M].Beijing: Publishing House of Electronics Industry, 2009: 131-132.)

[6] 房建成,宁晓琳,田玉龙.航天器自主天文导航原理与方法[M].北京: 国防工业出版社, 2006: 178-180.(FANG Jian-cheng,NING Xiao-lin,TIAN Yu-long. Spacecraft Autonomous Celestial Navigation Principle and Method[M].Beijing: National Defense Industry Press, 2006: 178-180.)

[7] 沈莹.机动目标跟踪算法与应用研究[D].西北工业大学, 2007: 9-21.

[8] 纪文涛.弹载GPS/SINS组合导航系统研究[D].南京理工大学, 2012: 39-45.

[9] 邱凯,黄国荣,陈天如,等.基于滤波过程的滤波发散判别方法[J].系统工程与电子技术, 2005, 27(2): 229-231.(QIU Kai,HUANG Guo-rong,CHEN Tian-ru,YANG Ya-li. Method of Divergence Detection for Kalman Filter Based on Filtering Process[J]. Journal of Systems Engineering and Electronics, 2005, 27(2): 229-231.)

[10] 徐定杰，贺瑞，沈锋,等.基于新息协方差的自适应渐消卡尔曼滤波器[J].系统工程与电子技术，2011，33(12):2696-2699.(XU Ding-jie,HE Rui,SHEN Feng, et al. Adaptive Fading Kalman Filter Based on Innovation Covariance[J]. Journal of Systems Engineering and Electronics, 2011,33(12):2696-2699.)

[11] 杨柳庆，肖前贵，牛研,等.基于渐消卡尔曼滤波器的定位系统设计[J].南京航空航天大学学报,2012,44(1):134-138.(Yang Liuqing,Xiao Qiangui,Niu Yan,et al. Design of Localization System Based on Reducing Kalman Filt[J]. Journal of Nanjing University of Aeronautics & Astronautics,2012,44(1):134-138.)

A Integrated Navigation System Design Based on Missile-Borne Multi-level Fault Tolerance

LEI Haoran CHEN Shuai CHENG Chen

School of Automation, Nanjing University of Science and Technology, Nanjing 210094，China

InviewoftheproblemsthattheprecisionoflooseintegratednavigationsystemdeclinesandthesystemevencannotworkwhenIMUandGPSareinabnormalstateinhighdynamicsituation,thevarioustypesofabnormalitiesthatmayoccurareanalyzedandtheappropriatetreatmentstrategiesaregivenindetail.Onthebasis,akindofmissile-bornemulti-levelfaulttoleranceintegratednavigationsystem(MFTINS)basedonDSP/FPGAhardwareplatformisdesigned,whichisappliedtotheintegratednavigationofanewmissile.Atthesametime,inordertosolvetheproblemthattheeffectofconventionalKalmanfilter(CKF)isnotsatisfactoryandevendivergent,theadaptiveKalmanfilter(AKF)isproposed.TheapplicabilityandeffectivenessofthedesignforintegratednavigationsystemandAKFisproventhroughtestsandanalyses.

Missile-borne;Multi-levelfaulttolerance;Integratednavigation;Highdynamic;Adaptivekalmanfilter

*国家自然科学基金(61104196);中央高校基本科研业务费专项资金资助(NUST2011YBXM117)

2013-04-22

雷浩然(1989-)，男，南京人，硕士研究生，主要研究方向为组合导航；陈 帅(1980-)，男，江苏南通人，博士，讲师，硕士研究生导师，主要研究方向为导航、制导与控制；程 晨(1981-)，男，南京人，硕士研究生，主要研究方向为组合导航。

V249.3

A

1006-3242(2013)05-0019-06