基于自适应模糊滑模的飞行器姿态控制系统设计

周连文 李芳华

上海航天控制技术研究所, 上海 200233



基于自适应模糊滑模的飞行器姿态控制系统设计

周连文 李芳华

上海航天控制技术研究所, 上海 200233

针对飞行器在大姿态角飞行时系统存在的非线性、耦合和不确定性因素，提出了自适应模糊滑模的控制方法来设计飞行器的姿态控制系统。采用模糊逼近的方法对姿态控制系统的不确定性进行补偿，并在此基础上设计了自适应模糊滑模解耦控制器。推导了系统的控制律和参数自适应律，并基于李亚普诺夫函数证明了该控制方法可保证闭环系统的全局稳定，最后通过数值仿真验证了本文提出方法的有效性。 关键词 飞行器；姿态控制；自适应模糊滑模；解耦控制

飞行器姿态运动方程是非线性的，通道间存在气动耦合，此外，由于飞行过程中，高度、大气密度等变化，系统中又存在很大的不确定性。传统的基于小扰动的控制方法存在着明显的不足，为此，Sang Yong Lee和DongKyoung Chwa等人采用了反馈线性化的方法设计了自动驾驶仪[1-2]。文献[3]在反馈线性化的基础上引入了神经网络，用以估计在不同气动特征点的控制律，文献[4]采用神经网络来估计系统中的未建模动态和外来扰动。文献[5]在自适应滑模控制中引入了最终吸引子做自适应模糊调节律。文献[6]对BTT导弹采用变结构解耦控制，但解耦控制并不是开始就起作用，而是系统进入理想滑动模态后才具有解耦效果。B.Yoo等利用模糊系统逼近未知函数，只要知道未知函数的边界，便可设计基于模糊的自适应滑模控制器[7]。本文针对飞行器姿态运动方程中存在的非线性、耦合和不确定性等特点，采用模糊逼近的方法对系统中的不确定性即参数不确定、未建模动态和外界干扰进行补偿，并设计了自适应模糊滑模解耦控制器。最后将本文的设计方法应用到飞行器大姿态角的控制系统设计中，取得了良好的控制效果。

1 飞行器的姿态运动方程

选取ϑ，ψ，γ，ωx，ωy，ωz为系统的状态变量，设x=[x1…x6]T，其中，x1=ϑ，x2=ψ，x3=γ，x4=ωx，x5=ωy，x6=ωz，输入为：u=[δxδyδz]T，输出为：y=[ϑψγ]T，则考虑参数不确定性和外来干扰的飞行器姿态运动状态方程为：

y=hx

(1)

具体表达式为：

2 自适应模糊滑模控制系统设计

首先对飞行器姿态运动方程进行坐标变换，并进行线性化，然后采用自适应模糊滑模的方法对系统进行设计。

令h1(x)，h2(x)和h3(x)表示hx的第1～3行，f为f(x)，设Φ为：

(2)

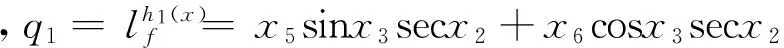
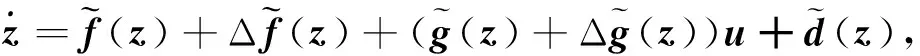
(3)

其中，z=[z1…z6]T，u=[u1u2u3]T，u1=δx，u2=δy，u3=δz。y=[y1y2y3]T，y1=z1=ϑ，y2=z3=ψ，y3=z5=γ。

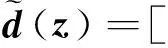
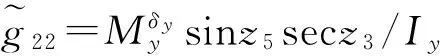
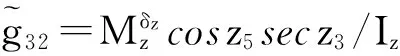
实际上，上面的表达式中，还含有x4，x5，x6。通过前面的z1～z6表达式可解算出：x4=(z6-z2sinz3)；x5=(z2cosz3sinz5+z4cosz5)；x6=(z2cosz5cosz3-z4sinz5)。将x4，x5，x6代入上面诸式，便构成完全由z表示的表达式。

(4)

其中，A(z)=A0(z)+ΔA(z)，B(z)=B0(z)+ΔB(z)+d(z)，

定义s为滑模向量，s∈R3，s=[s1s2s3]T。

(5)

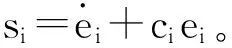
由于ΔA(z)，ΔB(z)，d(z)未知，即Δaij(z)，Δbi(z)，di(z)(i=1,2,3,j=1,2,3)未知，因此构造模糊逻辑系统来逼近未知函数Δaij(z)，Δbi(z)，di(z)。

(6)

(7)

(8)

其中，Υ1，Υ2，Υ3为自适应增益，定义最优参数为：

(9)

其中，l代表Δaij，Δbi，di，Ωl为θl的集合。定义最小逼近误差为：

(10)

设控制律为：

(11)

对于si,则有

定理1 假设1和2成立，对于非线性系统式(1)，控制律采用式(11)，自适应律采用式(8)，则系统全局渐进稳定。

证明：V(t)=V1(t)+V2(t)+V3(t)，

定理1能保证系统稳定，但其中k的确定必须先估计模糊系统所逼近的误差的上确界，而k又是符号函数的系数，所以k选择的不恰当，直接影响到控制量的切换幅度。为此可以自适应选择k，则式(11)改写为：

(12)

(13)

定理2 假设1和假设2成立，对于非线性系

统式(1)，控制律采用式(12)，自适应律采用式(8)和(13)，则系统全局渐进稳定。

3 仿真结果

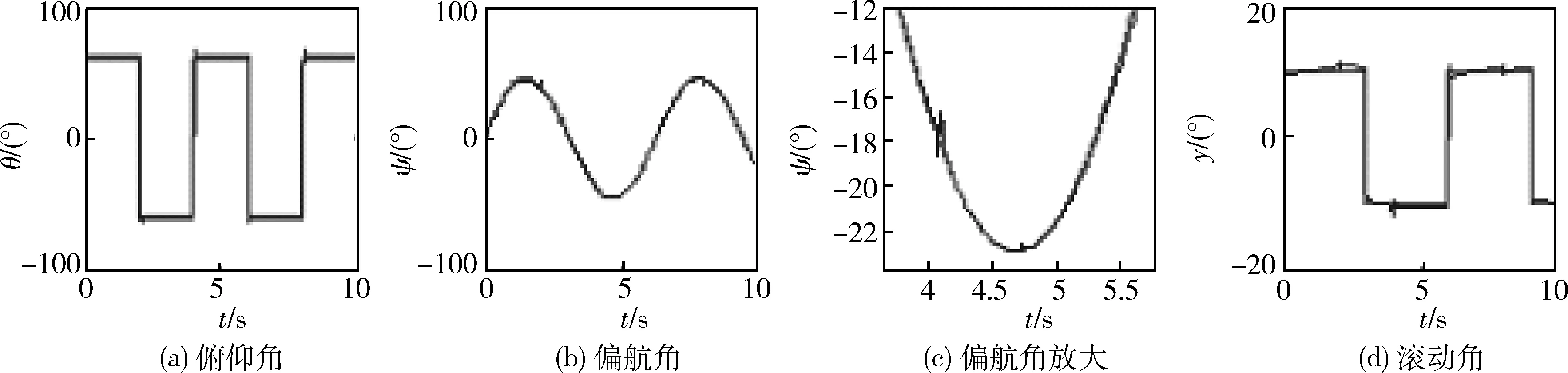
图1 采用自适应模糊滑模控制的姿态角跟踪曲线

图2 采用滑模变结构的姿态角跟踪曲线

4 结论

针对飞行器大姿态角飞行时，系统存在耦合、不确定的情况，采用模糊逼近的方法对系统中的不确定性进行补偿，并设计了自适应模糊滑模解耦控制器。仿真结果表明系统具有良好的解耦跟踪特性，并且可以很好地克服系统中存在的不确定性。

[1] Lee Sang-Yong, Lee Ju-Il, Ha In-Joong. Nonlinear Autopilot for High Maneuverability of Bank-to-Turn Missiles[J]. IEEE Trans on Aerospace and Electronic Systems, 2001, 37(4):1236-1253.

[2] DongKyoung Chwa and Jin Young Choi. New Parametric Affine Modeling and Control for Skid-to-Turn Missiles[J]. IEEE Trans on Control Systems Technology, 2001, 9(2):335-347.

[3] ZHAN L,LUO X S,ZHANG T Q. Decoupling Control Method Based on Neural Network for Missile[J]. Journal of Beijing Institute of Technology, 2005,14(2):166-169.

[4] 曹邦武,姜长生.一类不确定非线性系统的回馈递推滑模鲁棒控制器设计[J].宇航学报, 2005, 26(6): 808-822.(Cao Bang-wu, Jiang Chang-sheng. Robust Back Stepping Sliding Mode Controller Design Approach for a Class of Uncertain Nonlinear System [J]. Journal of Astronautics, 2005, 26(6): 808-822.)

[5] 薛月菊,杨士元,冯汝鹏.MIMO非线性自适应模糊滑模控制[J].哈尔滨工业大学学报,2003,35(1):97-100.(Xue Yue-ju, Yang Shi-yuang, Feng Ru-peng. Adaptive Fuzzy Sliding Mode Control Based on Terminal Attractors for MIMO Nonlinear Systems[J]. Journal of Harbin Institute of Technology, 2003,35(1):97-100.)

[6] 童春夏,王正杰,张天桥.BTT导弹的变结构解耦控制系统设计[J].宇航学报,2006,27(1):27-30 (Tong Chun-xia, Wang Zheng-jie, Zhang Tian-qiao. Decoupling System Design Based on Variable Structure System for BTT Missile[J]. Journal of Astronautics,2006,27(1):27-30.)

[7] Yoo B,Ham W. Adaptive Fuzzy Sliding Mode Control of Nonlinear System[J]. IEEE Trans. On Fuzzy System,1998,6(2): 315-321.

[8] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京理工大学出版社, 2000. (Qian Xing-fang, Lin Rui-xiong, Zhao Ya-nan. Flight mechanics of missile[M]. Publishing Company of Beijing Institute of Technology, 2000.)

[9] 胡跃明.非线性控制系统理论与应用(第2版)[M].国防工业出版社,2005.(Hu Yue-ming. Theory and Application of Nonlinear Control System (Second Edition)[M].National Defense Industry Press,2005.)

Design of Aircraft Attitude Control System Based on Adaptive Fuzzy Sliding Mode

ZHOU Lianwen LI Fanghua

Shanghai Institude of Spaceflight Control Technology, Shanghai 200233, China

Thereexistsnonlinearity,couplinganduncertaintywhentheaircraftflywithlargeattitudeangle.Forthissituation,themethodofadaptivefuzzyslidingmodecontrolisproposedtodesignattitudecontrolsystemoftheaircraft.Themethodoffuzzyapproachisadoptedtocompensatetheuncertaintyofthesystem,andthentheadaptivefuzzyslidingmodedecouplingcontrollerisdesigned.Thecontrollawandparameteradaptivelawareeducedinthepaper.Itisproventhatthewholecontrolschemecanguaranteethestabilityoftheclosed-loopsystem.Thesimulationresultsshowtheeffectivenessoftheproposedmethods.

Aircraft;Attitudecontrol;Adaptivefuzzyslidingmode;Decouplingcontrol

2013-02-06

周连文(1972-)，女，江苏响水人，博士，主要研究方向为飞行器导航、制导与控制；李芳华(1972-)，女，江苏丹阳人，硕士，主要研究方向为计算机仿真与控制。

V448.22

A

1006-3242(2013)05-0013-06