一个具有消息恢复的指定验证者的代理盲签名方案

胡小明,刘 琰,杨寅春,王 见,徐晓林

(上海第二工业大学计算机与信息学院,上海201209)

一个具有消息恢复的指定验证者的代理盲签名方案

胡小明,刘 琰,杨寅春,王 见,徐晓林

(上海第二工业大学计算机与信息学院,上海201209)

针对最近提出的若干具有消息恢复的指定验证者的盲签名方案,提出对这些方案的安全性分析。分析显示,这些方案都是不安全的,均不满足不可伪造性,攻击者能任意伪造签名。因此,这些方案都不能应用到如电子投票、电子货币等实际系统中。为了克服这些缺陷,提出了一个改进的具有消息恢复的代理盲签名方案,并对方案的安全性和有效性进行了分析。分析显示,提出的方案不仅安全而且有效。

密码学;盲签名;代理盲签名;消息恢复;指定验证者;安全分析

0 引言

1994年,Nyberg和Rueppel提出了具有消息恢复特性的数字签名[1]。在一个消息可恢复签名中,只有指定的签名接收者才能从得到的数字签名中恢复出签名的消息,从而保护签名的消息只有合法的用户才能看到。盲签名的概念最初是Chaum在1983年提出的[2]。在一个盲签名中,要求签名者在不知道被签文件内容的情况下对文件进行签名,以保护用户的隐私。盲签名的这种特性使得盲签名在电子现金、电子投票等协议中有着广泛的应用。将盲签名和消息可恢复签名结合,就是具有消息恢复功能的盲签名,它具有盲签名和消息可恢复签名的双重优点。因此,吸引了不少学者对其进行研究,提出了许多方案[3-9]。

最近(2011年),褚等[7]人基于离散对数问题提出了一个具有消息恢复的指定验证者的盲签名方案(以下简称褚-张方案),他们宣称他们的方案不仅有效而且是不可伪造的。同年(2011),俞等[8]人基于椭圆曲线离散对数问题也提出了一个具有消息恢复的指定接收者的盲签名方案(以下简称俞-谢方案),他们称方案是不可伪造的,而且具有很高的效率。但是,何等[9]学者在2012指出俞-谢方案是不安全的,指定验证者可以伪造盲签名。为了克服这个问题,何等学者提出了一个改进的方案,并宣称他们的方案是强不可伪造的。然而,本文将指出,不仅褚-张方案是不安全的,何等学者的改进方案同样也是不安全的。此外,本文还将指出俞-谢方案不仅存在何等学者指出的指定验证者伪造盲签名的缺陷,而且存在更为严重的缺陷。本文给出了一种攻击方法,攻击者使用这种方法后能在任意选择的消息上伪造签名。所以,这三种方案都是不安全的。为了克服这些问题,本文将提出一种改进的方案,并对方案的正确性、安全性和有效性进行了分析。

1 褚-张的方案回顾和安全性分析

1.1 褚-张的具有消息恢复的指定验证者的盲签名方案回顾

褚-张的方案[7]涉及三个参与方,分别是:签名请求者A、签名者B和指定签名接收者C,一共有三个阶段组成:系统建立阶段、签名生成阶段和签名验证阶段。为了方便讨论,我们采用与褚-张方案[7]同样的符号对方案进行描述。

系统建立阶段设p,q是满足q|p-1的两个大素数,g是GF(q)的一个本原元。随机选择三个整数xA, xB,xC∈,计算yA=gxAmod p,yB=gxBmod p,yC=gxCmod p,将(xA,yA)、(xB,yB)、(xC,yC)分别作为A、B、C的私钥和公钥对。公开系统参数为{p,q,g,yA,yB,yC}。

签名生成阶段设m是A要求签名的消息,为了建立m上的盲签名,A和B执行如下操作:B随机选择kB∈,然后计算rB=gkBmod p,并将rB发送给A;A随机选择两个盲因子a,b∈,然后计算rA=gbmod p,m′=mod p,并将m′发送给B;B计算s′=kB−q,将s′发送给A;A收到s′后,验证等式gs′=rBmod p是否成立。如果不成立,那么签名无效,签名结束。如果等式成立, A继续计算s=as′+b−xAmod q,m′′=am′mod p,r=mod p;那么(m′′,r,s)就是消息m上的盲签名,这个签名是发送给C且只有C能恢复消息。

签名验证阶段C收到签名(m′′,r,s)后,为了恢复消息,他计算m=mod p,这样C得到了消息m。

1.2 褚-张方案的伪造性分析

接下来我们将证明褚-张的上述方案不满足不可伪造性,在签名者B不知情的情况下,攻击者能伪造任意消息上的签名。为了分析方便,我们假设m*是攻击者选择的要伪造签名的消息,注意m*可以是攻击者选择的任何消息。为了伪造m*上的签名,攻击者执行如下操作。

首先,攻击者伪装成普通的签名请求者与签名者B发起一次正常的签名操作,要求B产生一个消息m上的盲签名(m/=m*)。攻击者和B按照上述的过程交互执行,最终攻击者得到m上的一个盲签名(m′, s′)。我们把攻击者和B交互过程中产生的参数表示为(kB,a,b,rA,rB),其中攻击者能看到参数是(a,b, rA,rB,m′,s′),攻击者把这些参数记录下来。

在得到了(a,b,rA,rB,m′,s′)后,攻击者开始伪造m*上的签名。首先,攻击者计算

然后,设两个盲因子a*=m*-1ma,b*=b,并计算

那么,(s′*,m′*)就是消息m*的一个签名。这个签名是正确的,因为

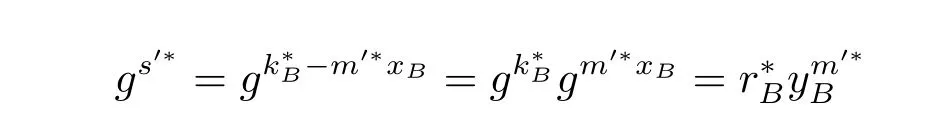
(s′*,m′*)满足验证等式gs′=mod p,所以是一个有效的签名。

假设攻击者想把消息m*发送给指定的接收者C,那么攻击者只需计算s*=a*s′*+b*−xAmod q, m′′*=a*m′*mod p,r*=mod p,那么(m′′*,r*,s*)就是消息m*上的盲签名,然后攻击者把(m′′*, r*,s*)发送给C。

C收到(m′′*,r*,s*)后,按照原方案的操作计算m*=mod p,这样C就可以恢复出消息m*了。

C能根据(m′′*,r*,s*)恢复出消息m*,因为

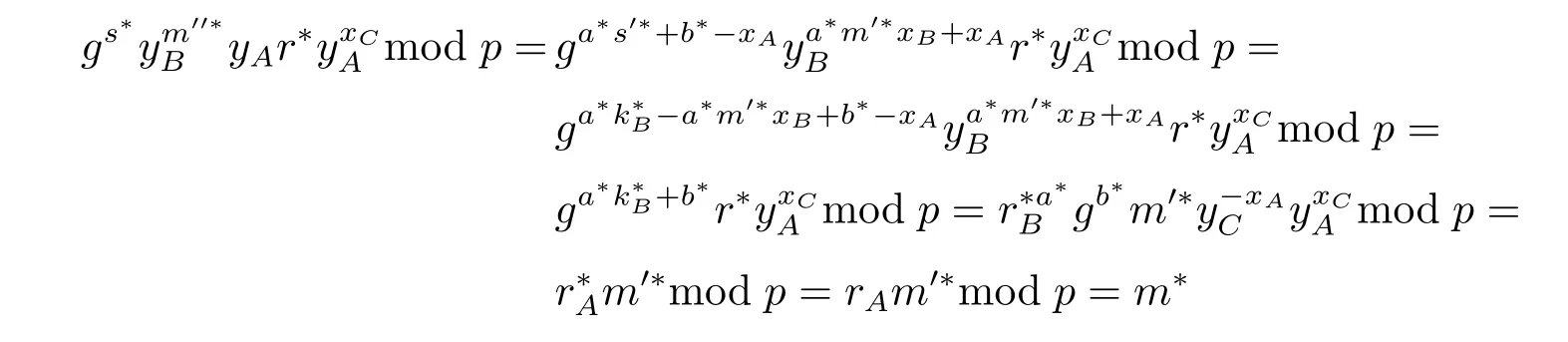
综上,(m′′*,r*,s*)是一个有效的指定验证者的盲签名,攻击者伪造成功。所以,褚-张的方案不安全。

2 俞-谢及其何等改进方案的回顾和安全性分析

2.1 俞-谢的具有消息恢复的指定验证者的代理盲签名方案回顾

俞-谢的方案[8]有四个阶段:系统初始化阶段、代理密钥产生阶段、代理签名生成阶段和签名验证阶段。一共涉及四个参与方:原始签名者A、代理签名者B、签名请求者C和指定验证者D。为了讨论方便,我们采用与俞-谢方案同样的符号来描述方案,具体方案如下。

系统初始化阶段假设G1和G2分别是两个阶为素数q的加法和乘法群,e:G1×G1→G2是一个双线性映射,P是G1的一个生成元。H1:{0,1}*×G1→是一个强无碰撞安全哈希函数。A、B、C和D分别随机选择kA,kB,kC,kD∈,将(PA=kAP,kA),(PB=kBP,kB),(PC=kCP,kC),(PD=kDP, kD)作为自己的公私钥对。公开系统参数{e,G1,G2,q,P,H1,PA,PB,PC,PD}。

代理密钥产生阶段首先,原始签名者A制定一个代理授权证书mw,其中包含原始签名者和代理签名者的身份信息、代理期限、代理签名的内容等。然后,A随机选择k∈,并计算rA=kP=(xr,yr), rx=xr,e1=H1(mw‖rx‖PA),SA=kAe1+k,PAB=SAP+PBe1,将(rA,PAB,SA,mw)发送给代理签名者B;B收到后,计算rx=xr,e1=H1(mw‖rx‖PA),然后验证等式SAP=e1PA+rA和PAB=SAP+PBe1是否成立。如果不成立,则结束签名。如果成立,B计算kAB=SA+kBe1作为代理签名密钥。

代理签名生成阶段假设m是签名请求者C要求盲签名的消息,为了得到m上的盲签名,C和B执行如下操作。

B收到¯m后,计算S′=kAB¯m,把S′发送给C。

C收到S′后,验证等式e(aS′,P)=e(¯mPD,PAB)是否成立。如果不成立,签名结束。如果成立,C接着计算S=aS′+kCPD。那么,(mw,rA,¯m,S)就是消息m上的签名。

签名验证阶段验证者D收到签名(mw,rA,¯m,S)后,验证下式(1)

是否成立。如果不成立,则签名无效。如果等式成立,D计算m=(¯m+(kDPC)x)(PB)-1x恢复消息m,然后通过下式(2)

验证签名的有效性。

2.2 俞-谢方案的伪造性分析

接下来我们证明俞-谢的上述方案不满足不可伪造性,攻击者能伪造任意消息上的签名。我们假设m*是攻击者选择的要伪造签名的任何消息。为了伪造m*上的签名,攻击者执行如下操作。

首先,攻击者伪装成普通的签名请求者与签名者B发起一次正常的签名操作,要求B产生一个消息m上的盲签名(m/=m*)。攻击者和B按照上述的过程交互执行,最终攻击者得到m上的一个签名(mw,rA, m,S)。我们把在交互过程中产生的参数表示为(kAB,a,m,m,S′,S),其中攻击者能看到参数是(a,m,m, S′,S),攻击者把这些参数记录下来。

攻击者在得到了(a,m,m,S′,S)后,计算

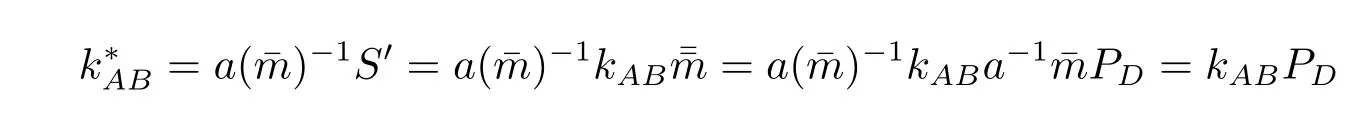
那么,(mw,rA,¯m*,S*)就是m*上的盲签名。这个伪造的签名是有效的,因为

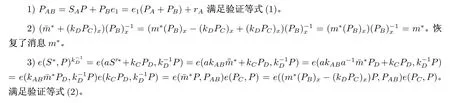
综上,(mw,rA,¯m*,S*)就是一个有效的指定验证者的盲签名,攻击者伪造成功。所以,俞-谢的方案不安全。

2.3 何等改进方案的回顾

何等[9]学者的基于俞-谢方案的改进方案由以下几部分组成,为了分析方便,本文采用与何等学者的方案类似的符号描述方案。

系统初始化阶段同俞-谢的方案,系统公开的参数为{G1,G2,q,P,H1,PA,PB,PD}。

代理密钥产生协议阶段A随机选择k∈R,设置RA=kP,e1=H(mw‖RA),sA=kAe1+k,把(RA,sA,mw)发送给B;B收到后,设置代理签名密钥和公钥为(kAB,PAB),其中kAB=sA+kBe1, PAB=kABP=e1(PA+PB)+RA。

代理签名生成算法阶段C随机选择k1,a∈R计算R=k1P,¯m=m(PB)x−(k1PD)x,¯m= a-1¯mPB并将¯m发给B;B收到后,发送(RA,S′,mw)给C,其中S′=kAB¯m;C验证通过后,计算S=aS′+k1PD。那么,(RA,mw,¯m,R,S)就是代理盲签名。

代理盲签名验证阶段D收到(RA,mw,¯m,R,S)后,用m=[¯m+(kDR)x][(PB)x]-1恢复消息m,用e(S,P)=e(PB,PAB)¯me(PD,R)验证签名的有效性。

2.4 何等改进方案的伪造性分析

接下来我们证明何等学者的上述改进方案仍然不满足不可伪造性,攻击者能伪造任意消息上的签名。攻击的操作步骤和攻击俞-谢方案的操作步骤类似,具体操作如下。

首先,攻击者随机选择一个消息m,并与B进行一次正常的代理盲签名操作,要求B返回一个m上的有效的代理盲签名(RA,mw,¯m,R,S)。攻击者记录这个过程中产生的参数(a,¯m,¯m,S′,S)。

然后,攻击者选择一个要伪造代理盲签名的消息m*(/=m),并计算

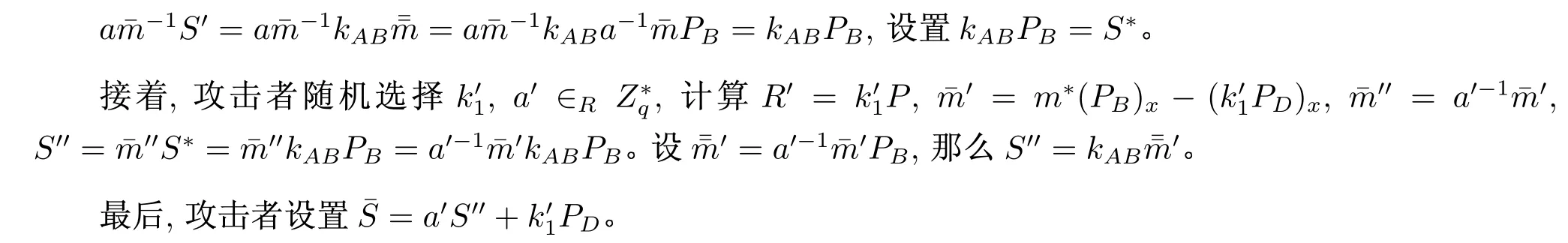
那么,(mw,RA,¯m′,R′,¯S)就是攻击者伪造的消息m*上的代理盲签名。这个签名是一个有效的签名,因为指定验证者D收到(mw,RA,¯m′,R′,¯S)后,用如下方法恢复消息m*:

用如下方法验证消息的有效性:

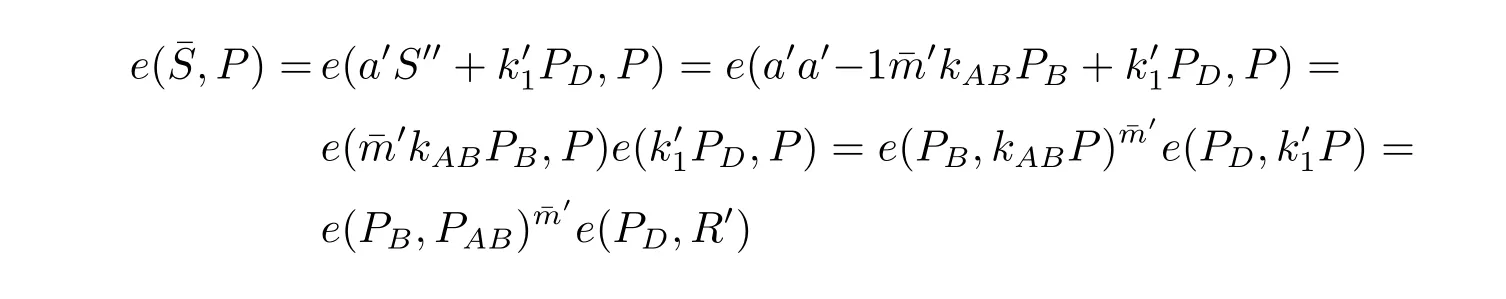
综上,(mw,RA,¯m′,R′,¯S)就是一个有效的指定验证者的盲签名,所以攻击者伪造成功,何等学者的方案是不安全的。

3 本文改进的方案

3.1 提出的方案

为了抵御上面提出的攻击,本文基于何等学者的代理盲签名方案,提出一个改进的具有不可伪造性的代理盲签名方案,具体的设置如下。

系统初始化阶段同何等学者的方案,系统公开的参数为{G1,G2,q,P,H1,PA,PB,PD}。

代理密钥产生协议阶段同何等学者的方案,设置的代理签名密钥和公钥为kAB=sA+kBe1, PAB=kABP=e1(PA+PB)+RA。

代理签名生成算法阶段C随机选择k1∈R设置R=k1P,¯m=m(PB)x−(k1PD)x。然后,随机选择a∈R,计算¯m=a-1¯mPB,Y=a-1PA并将(¯m,Y)发给B;B收到后,计算S′=kAB¯m+kABY,并将S′发送给C;C收到S′后,首先计算PAB=e1(PA+PB)+RA,然后验证等式e(S′,P)=e(PAB,¯m+Y)是否成立,如果成立,则签名有效,C计算S=aS′+k1PD。那么,(RA,mw,¯m,R,S)就是最后产生的代理盲签名。

代理盲签名验证阶段指定验证者D收到消息m上的代理盲签名(RA,mw,¯m,R,S)后,用m=[¯m+(kDR)x][(PB)x]-1恢复消息m,并判断恢复的消息是否符合授权证书mw中的规定。如果符合,那么用如下等式验证盲签名是否有效:

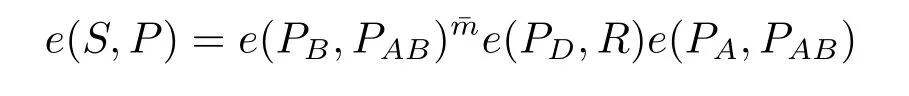
如果等式成立,那么签名有效,否则无效。

3.2 方案分析

(1)正确性分析

指定验证者验证:获得的代理盲签名(RA,mw,¯m,R,S)只能由指定的验证者D进行验证,这是因为,消息m的恢复m=[¯m+(kDR)x][(PB)x]-1需要使用kD。而kD是指定验证者D的私钥,只有D知道,其他任何人都不可能知道。所以,只有D能恢复消息m。

正确性:提出方案的正确可以通过以下的推导过程进行证明。

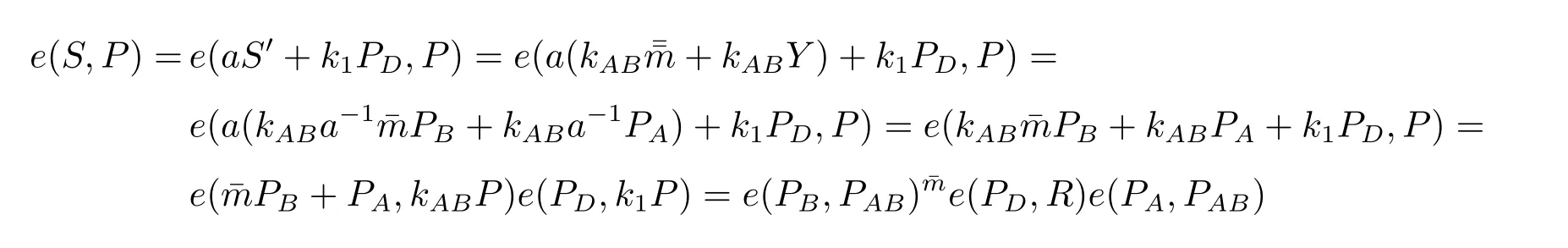
从以上的推导过程可以看出,只要按照本方案的设计进行代理盲签名,那么最后获得的代理盲签名一定能满足验证方程,即得到的代理盲签名是正确的。

(2)安全分析

提出的方案满足不可伪造性、盲性、可区分性、可验证性、不可滥用性等其他代理盲签名的安全特性。分析的方法和何等学者的方法类似。

不可伪造性:上面提出的方案能克服前面提出的攻击,是不可伪造的。如果攻击者想获得kABPB,那么他只能通过S′=kAB¯m+kABY获得。而要从S′中计算获得kABPB,攻击者必须先获得kABPA,但是攻击者不知道kAB,所以攻击者无法获得kABPA,从而也就不能得到kABPB。所以,本方案能抵御本文提出的攻击。

盲性:代理签名者B所签名的消息¯m是经过签名请求者C用盲化因子a盲化后所得的消息。因此,如果代理签名者B不知道盲化因子a,那么B不可能知道他所签名信息的原始消息是什么。

可区分性、可验证性、不可滥用性:代理签名者B所签名的消息中包含授权证书mw,而mw中一般包含原始签名者和代理签名者的身份信息、授权的日期范围、授权代理签名的消息内容等。因此,它能防止代理签名者滥用签名权利去签一些没有授权的消息。此外,代理签名中包含mw,所以任何人很容易区别原始签名和代理签名,也很容易验证代理签名是否得到原始签名者的许可。

(3)有效性分析

我们把提出的方案和俞-谢方案以及何等学者的方案就代理密钥生成、代理盲签名生成和代理签名验证这三个主要阶段的占主要成分的计算量进行比较。用P表示一次对操作,E表示一次指数操作,M表示一次乘法操作,A表示一次加法操作。

从表1可以看出,我们提出的方案与何等学者的方案相比,在代理密钥生成阶段具有同样的计算复杂性,但相比于俞-谢方案,本方案的计算量更少。在代理盲签名生成阶段,虽然与俞-谢方案和何等学者的方案相比,本方案多了两个乘法操作和两个加法操作,但在代理签名验证阶段,本方案比何等学者的方案少了一个乘法和两个加法,比俞-谢方案少了3个乘法和3个加法。因此,综合签名的所有阶段,本方案和俞-谢方案以及何等学者的方案几乎有相同的计算复杂性。注意,虽然本方案在代理签名阶段多了一个对操作e(PA,PAB),但这个对操作中的参数PA和PAB是系统发布的参数,所以这个对操作可以预计算,因此基本不花费时间。

表1 计算性能比较Tab.1 Cmparison of computational performance

综上,本文提出的改进方案,在不降低安全性的前提下基本没有增加计算量,所以是一个安全而有效的代理盲签名方案。

4 结论

本文首先对最近提出的若干具有消息恢复的指定验证者的盲签名方案进行了回顾,然后对这些方案的安全性进行了分析。分析表明这些方案都存在着安全缺陷,攻击者能够在签名者不知情的情况下对他自己选择的任何消息进行伪造签名。所以,这些方案虽然效率较高,但是不具有应用价值。针对存在的问题,本文在不影响效率和安全性的情况下,设计了一个真正有效且安全的具有消息恢复的指定验证者的盲签名方案。

[1]NYBERG K,RUEPPEL R A.Message recovery for signature schemes based on the discrete logarithm problem [C]//Advances in Cryptology-Eurocryp’94.Springer Berlin Heidelberg:Springer-Verler,1995.

[2]CHAUM D.Blind signatures for untraceable payments[C]//Advances in Cryptology-Crypto’82,NY:Plenum Press, 1983.

[3]黄振杰,王育民,陈克非.Nyberg-Reuppel消息恢复盲签名的一般化和改进[J].通信学报,2005,26(12):131-135.

[4]张学军.高效的基于身份具有消息恢复的盲签名[J].计算机工程与应用,2008,44(32):19-21.

[5]WEN Y,ZHANG F G,XU L L.Unlinkable secret handshakes from message recovery signature[J].Chinese Journal of Electronics,2010,19(4):705-709.

[6]RAJARAM RAMASAMY R,AMUTHA PRABAKAR M.Digital signature scheme with message recovery using knapsack-based ECC[J].International Journal of Network Security,2011,12(1):12-17.

[7]褚万霞,张建中.具有消息恢复的指定接收者的盲签名方案[J].计算机工程与应用,2011,47(13):72-73,153.

[8]俞建英,谢琪.具有消息恢复的指定验证者的代理盲签名[J].计算机应用与软件,2011,28(2):28-29,82.

[9]何俊杰,孙芳,祁传达.带消息恢复功能的代理盲签名方案分析与改进[J].计算机工程,2012,38(15):119-122.

A Proxy Blind Signature Schemes of Designated Verif i er with Message Recovery

HU Xiao-ming,LIU Yan,YANG Yin-chun,WANG Jian,XU Xiao-lin
(School of Computer&Information,Shanghai Second Polytechnic University, Shanghai 201209,P.R.China)

The security of two blind signature schemes designated verif i er with message recovery proposed recently is analyzed.The analysis shows that both schemes are not secure and do not satisfy the property of unforgeability,allowing an attacker to forge on any message.Both schemes can not be applied to real systems such as electronic voting and electronic cash.In order to overcome this drawback,an improved proxy blind signature scheme with message recovery is proposed,and the security and efficiency of the scheme is analyzed.The analysis shows that the proposed scheme is both secure and efficient.

Cryptography;blind signature;proxy blind signature;message recovery;designated verif i er;security analysis

TP309

A

1001-4543(2013)02-0086-07

2013-01-28;

2013-04-11

胡小明(1978–),女,讲师,博士,研究方向为密码学、信息安全,电子邮箱xmhu@sspu.cn。

国家自然科学基金资助项目(No.61103213);上海市教育委员会科研创新资助项目(No.10YZ201)