电导增量法在光伏系统MPPT中的研究
2013-08-16季亚鹏孙万鹏
季亚鹏,付 蓉,孙万鹏
(南京邮电大学 自动化院,江苏 南京210023)
在光伏系统中,光伏电池具有非线性特征,并且其输出受光照强度、环境温度影响较大。为了提高效率,目前广泛采用的技术是最大功率点跟踪MPPT(maximum power point tracking)。为了达到更好的稳定性和更快的跟踪速度,光伏电池MPPT控制一般选用电压控制方式。其中Boost电路采用的是输入端电压控制方式,即在输出端电压基本恒定的情况下,通过调节占空比来调节输入端电压。
[1-3]对电导增量法在MPPT中的应用进行了详细地论述,但缺少对最大功率点的跟踪过程及Boost升压电路的分析。本文首先分析了光伏电池的输出特性,然后通过Matlab/Simulink建立了整个光伏系统模型并进行仿真。分析了定步长电导增量法中步长的取值对系统稳定性和快速性的影响,并且阐述了在该方法下功率输出出现振荡的原因,使用变步长的电导增量法,改善了定步长的缺点。最后考虑外部环境的变化,对仿真结果作出了详细的分析,通过其P-V曲线,再现了系统进行最大功率点跟踪的整个过程。
1 光伏电池特性
1.1 光伏电池理论模型
光伏电池等效电路如图1所示[1]。

图1 光伏电池等效电路
设定图中所示的电压、电流正方向,可以得出光伏电池的I-V方程为:

在式 (1)中,Iq为光电流;Isat为二极管反向饱和电流;q为电子电荷 (1.6×1019C);K为玻耳兹曼常数 (1.38×10-23J/K);T为绝对温度;A为二极管因数;Rs为串联电阻;Rp为并联电阻。
1.2 光伏电池输出特性
由于光伏元件为非线性元件,不能用一个固定的数值或简单的方程式来表示其电压与电流之间的关系。所以,光伏电池的输出特性可用曲线的形式表示[4],如图2所示。

图2 光伏电池的输出特性曲线
图中 Isc、Voc、Im、Vm和 Pm分别为太阳电池的短路电流、开路电压、最大功率点电流、最大功率点电压和最大功率点功率。由图2可知,在光伏电池的输出电压比较小时,输出电流的变化量也非常小。随着输出电压的上升,输出电流逐渐减小,当输出电压上升到一定值时,输出电流急剧下降,在这个过程中,存在一个最大功率点Pm,在此点工作的太阳能电池输出功率最大。
2 用于MPPT的Boost电路原理
最大功率跟踪控制中常用的DC/DC变换器是Buck和Boost电路。由于Buck电路的输入端工作在断续状态下,若不加入储能电容,则光伏电池工作时断时续,不能处于最佳工作状态。相比之下,Boost电路只要输入电感足够大,可始终工作在输入电流连续状态。考虑到实际使用的光伏电池输出电压不高,则采用Boost升压电路比较合适[5]。
由图3可知,Boost电路是由功率开关 S、二极管 D、电感L、电容C和负载电阻R构成。Boost电路输入输出电压关系为:


图3 Boost升压电路原理图
由于占空比D恒小于1,所以输出电压始终大于输入电压,故该变换器称为升压变换器。
3 MPPT算法
MPPT算法是一个自寻优的过程[6]。通过实时检测光伏电池的输出电压与电流,不断改变系统工作点,比较光伏阵列前后的功率输出情况,从而逐步搜索出当前阵列的最大功率点。
3.1 定步长电导增量法
由图2可知,太阳能电池P-V特性是一单峰值曲线,电压由零逐渐增大,dP/dV的数值由大于零变到小于零,当dP/dV=0时取得最大功率Pm。
对P=VI,两边同时对V求导得:


式(4)为在MPP处的条件。图4为固定步长电导增量法的流程图,图中ΔD的大小固定使得不能同时兼顾MPPT的快速性和稳定性。

图4 定步长电导增量法控制流程图
3.2 变步长电导增量法
理论上,电导增量法能实现最大功率点的跟踪,但实际中由于系统一般处于动态过程,dP/dV为0的情况很少出现,所以即使在稳态环境中也存在一定的振荡。而变步长的电导增量法能改善这一问题。而且占空比跟踪步长可变,其中变步长的系数取自dP/dV的绝对值;当工作点远离MPP时,加大步长,加快跟踪速度;当工作点在MPP附近时,减小步长,以减小波动导致的功率损失。所以变步长电导增量法可表述为:

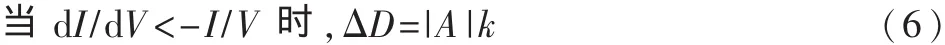


式中,k为占空比变化固定分量,A为步长控制常数。
4 仿真结果及分析
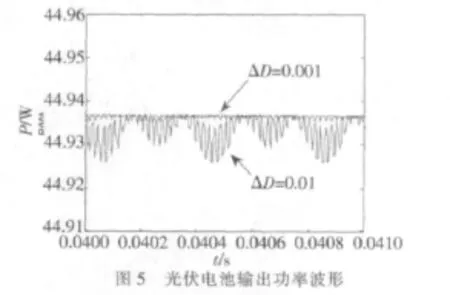
设定初始条件为标准光照1 kw/m2和常温25℃。在初始条件下,设定电导增量法步长为0.01,测得其到达相对稳定的状态所需时间为5 ms。把步长设为0.001后,测得其到达相对稳定的状态所需时间为32 ms。两次仿真波形如图5所示。由此可见,定步长电导增量法只能使得系统跟踪到最大功率点附近,在其周围振荡,只是步长不同振荡幅度不同而已。
虽然当步长比较小时,系统跟踪到最大功率点附近的时间变长,但是系统在最大功率点附近工作时的振荡比较小,对系统功率的损失影响比较小。当步长比较大时,虽然系统跟踪到最大功率点附近的速度比较快,但是当系统保持在最大功率点附近工作时,功率振荡比较大。经过以上分析可得,步长较大时,系统的动态性能比较好;步长较小时,系统的稳态性能比较好。所以,固定步长电导增量法不能同时兼顾MPPT的快速性和稳定性。采用变步长的电导微增法可以有效改善这种情况。
为了研究温度和光照强度变化对MPPT算法的影响,分别改变温度和光照,得出光伏电池电压、电流的仿真波形如图6所示。

当光照强度不变时,系统在0.03 s时给外界温度一个扰动,由25℃突变为 50℃,输出电压和电流的波形分别如图 6(a)、(b)中标号为 1的曲线所示。可见,温度的改变对于最佳工作电压影响较大,对最佳工作电流影响较小,符合太阳能电池输出特性。
当温度不变时,系统在0.03 s时给外界光照强度一个扰动,由1 000 W/m2突变为800 W/m2,输出电压和电流的波形分别如图 6(a)、(b)中标号为 2的曲线所示。可见,光照的改变对最佳工作电流影响较大,电流随光照减弱而减小,对最佳工作电压影响较小,符合光伏电池的输出特性。
通过Matlab/Simulink的仿真分析得出,电导增量法在最大功率点附近都有一定的振荡,而变步长电导增量法能大幅度减小在最大功率点附近的振荡。在外界环境相对稳定的情况下,变步长电导增量法控制具有良好的稳定性,使系统稳定工作在最大功率点;当外界环境突变时,变步长电导增量法能准确快速地跟踪到太阳电池的MPP,具有良好的快速性。
参考文献
[1]汤济泽,王丛岭,房学法.一种基于电导增量法的MPPT实现策略[J].电力电子技术,2011,45(4):73-75.
[2]原敬磊,张建成.一种改进的变步长电导增量光伏电源MPPT 控制方法[J].电网与清洁能源,2012,28(1):75-79.
[3]董密,杨建,彭可,等.光伏系统的零均值电导增量最大功率点跟踪控制[J].中国电机工程学报,2010,30(21):48-53.
[4]MUTOH N, OHNO M, INOUE T.A method for MPPT controlwhile searching forparameters corresponding to weather conditionsforPV generation systems[J].IEEE Transactions on Industrial Electronics, 2006, 53 (4):1055-1065.
[5]GLASNER I.Advantage of boost vs buck top-ology for maximum power point tracker in PV system[R].Nineteenth Convention of Electrical and Electronics Engineers.1996:335-358.
[6]HUSSEIN K H.Maximum photovoltaic power tracking:an algorithm for rapidly changing atm- ospheric conditions [J]. IEEE Proceedings of Generation Transmission and Distribution, 1995, 142(1): 59-64.
