海森堡：以美为媒的诺贝尔奖荣膺者

程民治，陈海波

（巢湖学院 物理系，安徽 巢湖 238000）

沃尔纳·卡尔·海森堡（Werner Karl Heisenberg,1901-1976）在纯学术方面所取得的举世瞩目的伟大功绩，及其在国际物理学界所处的崇高地位，是毋庸置疑绝无争议的。这正如曾经担任过N·玻尔文献馆（NBA）馆长的伊瑞克（Erik Rudinger）所断言的那样，海森堡是20世纪第三位最伟大的物理学家，泡利 （W.Pauli,1900-1958）和狄拉克（P.A.M.Dirac，1902-1984）都得靠后。不仅如此，海森堡还以他丰富而深邃的科学美学思想、新颖而独特的研究风格和科学方法，为我们留下了宝贵的科学哲学遗产。它必将对21世纪的物理学产生巨大而深远的影响。本文拟就他辉煌的科学人生，作一简要的论述。

一、坎坷幸运成果辉煌的科学人生

1901年12月5日，海森堡出生于德国的维尔茨堡。其父是古语文学家，原在中学任教，后来在慕尼黑大学担任希腊语教授；他的母亲也是一位古语言学家的女儿。因此，海森堡从孩童时代开始，就深受来自家庭古代文学氛围的耳濡目染。海森堡自幼天资聪颖，从上小学时就成绩优异，学习毫不费力。1918年春天，由于家境贫困，他曾被迫停学一年，到当地的一个农场从事体力劳动，以赚些钱来补贴家用。从那时起，海森堡就立志研习康德哲学。他一生酷爱音乐，擅弹钢琴。欧战结束后，在发生于德国的一次地方性战乱中，海森堡曾替军队干过装子弹和放哨之类的工作，并参加了后来兴起的“青年运动”，这实际上是青年们集合在一起徒步旅行。这也使他打上了追求简单、真实和与世俗决裂的烙印，对他的成长起了重要作用。但是，海森堡很快将自己的志趣转向了科学和哲学，自学了韦尔（H.Weyl）的《空间、时间与物质》一书，并接触了原子的概念。

1920年中学毕业后，海森堡进入慕尼黑大学就读，在名师索末菲（A.J.W.Sommerfeld）的指导下学习理论物理学，并很快就显示出了他非凡的科学才能。1922年夏，他随索末菲到格廷根听玻尔讲学（N.Bohr），他在讨论中的精彩发言引起了玻尔的高度关注，这就是海森堡和玻尔结交的开始。1923年，他在格廷根大学以一篇关于流体力学的论文获得博士学位，同年赴格廷根大学当玻恩（M.Born）的助教，深得玻恩的赏识。1924年7月，他又以一篇关于塞曼效应的论文取得了大学授课的资格。同年9月，他按照原先与玻尔的约定，去了哥本哈根随玻尔研究量子力学。1925年发表矩阵力学原理，其时他年仅23岁。1927-1942年任莱比锡大学理论物理学教授。1942年4月起海森堡就任柏林物理研究所所长，二战后曾担任洪堡基金会主席多年，他还担任过德国科学研究会主席，后于1970年退休。从1975年起，他的健康状况日见衰退，最终于1976年2月1日在慕尼黑家中逝世，享年75岁。他的一生荣获了包括诺贝尔物理学奖在内的许多荣誉。

综观海森堡四分之三个世纪的人生旅程，一方面，他经历了社会上的许多动荡，加之从小家庭经济状况入不敷出，以至于耽误了他的学业，这势必会给他的学术研究带来一定的损失。从这个角度看，海森堡的科研生涯是坎坷的。但是在他成才的关键时刻，荣幸地得到了当时国际物理学界的三位巨头与名师——索末菲、玻恩、玻尔的器重、指导与教诲。因此，从这个方面而言，他又是幸运的。诚如海森堡后来回忆时所说：“我在索末菲那里学到了乐观精神，在格廷根学到了数学，在玻尔那里学到了物理学。”①弋革：《W·海森堡的学术和人品》，《自然辩证法通讯》（京）1990年第1期,第63-64页。

统览海森堡的科研人生，成果颇丰，业绩卓著。主要包括：

其一，早期成果。就在海森堡当年进入慕尼黑大学攻读理论物理学期间，在索末菲的指导下，他于1921-1922年间完成了三篇论文。其中第一篇处理了原子的双重态和三重态的塞曼效应，其余两篇是和索末菲合撰的，系统讨论了原子多重谱线的宽度和强度等问题。1922年冬，在玻恩的指导下，海森堡又完成了两篇处理多电子原子特别是氦原子的结构的论文。他的另外两篇论文就是上文中所提及的博士论文与取得大学授课资格的论文。

其二，1924年海森堡在丹麦工作期间，为了更好地表述恩师玻尔所提出的对应原理，他和克喇末（W.Klemm）一起系统地研究了原子对光的色散问题，并共同推广了拉登堡（R.Ladenburg）的理论，得出了极其重要的色散公式。这一工作实际上打开了通往矩阵力学的门径。

其三，矩阵力学的创建。海森堡发现，旧量子论所依赖的多是电子的位置和绕行周期等一些不可观察的量，这或许正是它陷入重重困难的基本原因。于是，海森堡决定抛弃玻尔那种对原子所作出的形象化的描述，开始着眼于一些以辐射频率和强度等可直接观察量为基础，来创立他的新的量子理论。1925年7月25日，他将研究结果以题为《关于运动学和动力学关系的量子论新解释》②Heisenberg W.über Quantentheoretische ümdentung Kinematischer and Mechanis-her.Zeit Phys,1925,33,PP.879-893.的开拓性论文予以发表。并在该文的提要中明确指出：“本文试图仅仅根据那些原则上可观察的量之间的关系来建立量子力学理论基础。”海森堡甚至还坦率地承认：“矩阵力学可以看成用定量关系来代替玻尔对应原理的定性关系的一种成功的尝试。”③海森堡：《二十世纪物理学中概念的发展》，《现代物理学参考资料(第3集)》北京：科学出版社,1978年，第24页。正是这一划时代的伟大贡献，标志着量子力学的正式创立，这一天也被称为“量子力学诞生日”。1932年海森堡也因创立了量子力学，尤其是它的应用导致了发现氢的同素异形体而荣登诺贝尔奖的领奖台。

此外，海森堡还将探索的目光，投射到诸如量子电动力学、原子核、宇宙射线中的簇射和介子的产生、统一场论、流体中的湍流、超导性等领域，并取得了一些重要的成果，发表了数十篇学术论文。海森堡一生的主要科学著作有：《论运动学关系式和力学关系式的量子论诠释》、《量子力学中的多体问题和共振》、《论量子理论的运动学和力学的直观内容》、《量子力学的发展》。④郭奕玲，沈慧君：《诺贝尔物理学奖一百年》，上海：上海科学普及出版社,2002年，第125页。

二、在科学探索的征途上与美偕行

深受古希腊毕达哥拉斯数学学派思想影响的海森堡⑤W·海森堡：《物理学和哲学》，范岱年译，北京:商务印书馆,1984年。，从小就是沐浴着家庭浓郁的古代文学的阳光雨露成长起来的，加之他终生爱好音乐，弹得一手好钢琴，自然深知科学与艺术之间决非风马牛互不相及。他曾形象地将它们比作是人类语言中不同的词和词组。他说：“科学和艺术二者在许多世纪的历程中形成了人类的一种语言，用这种语言我们能够谈论实在的更为微小的部分，而各种概念的前后一贯的集和不同的的艺术风格是这种语言中不同的词和词组。”①W·海森堡：《物理学和哲学》，范岱年译，北京:商务印书馆,1984年，第64页。虽然“海森堡年轻时没有很多数学的修养，可是量子力学发现后，尤其他晚年时，见解有些改变。他了解到数学在物理中有一个非常重要的地位，……用这个数学能做出我们所做不出的东西。”②杨振宁：《美与物理学》，《浙江大学学报》（社科版）1998年第3期，第1-8页。针对利用数学结构能创造出科学奇迹,海森堡还比较了物理学中广为使用的数学方法和建造中世纪大教堂的各种手艺人的艺术风格的基本要素，诸如相等与不相等、重复与单一、对称与变化、一与多、一定的结构方式与图形，特别是黄金分割律与极值原理，等等。认为这些基本的数学概念与原理，无论在艺术还是在自然科学中，都在起着本质的作用。于是，他得出了这样一个结论：“精密科学与艺术的类似变得极为显而易见了。”③W·海森堡：《精密科学中美的含义》，曹南燕译，《自然科学哲学问题丛刊》1982年第1期，第40-47页。“科学和艺术的两种过程，并非迥然不同。”④W·海森堡：《物理学和哲学》，范岱年译，北京:商务印书馆,1984年，第64页。

基于海森堡认为科学与艺术间相似相通的真知灼见，并以他长期从事物理学研究的亲身体验，明确地指出了那种将“美”限制在有形有象的事物上的观点，显然是片面的。因为在他看来，在人类的文明中还存在着另一个美的广阔天地，这就是在自然科学中所呈现出的“美”。他说：在“整数和几何形式”之中，“有些东西很美的这种印象完全是直接的，这无需作任何辩护和解释。”⑤W·海森堡：《精密科学中美的含义》，曹南燕译，《自然科学哲学问题丛刊》1982年第1期，第40-47页。因此，“虽然‘美的’（或‘精巧的’）这个表示性质的形容词在这里确实是用来表征艺术的特性的 ，但美的王国却远远延伸到艺术领域之外。它无疑也包括精神生活的其他领域；自然美也反映在自然科学的美之中”，尤其是体现在数学美之中。海森堡非常赞赏开普勒（Johannes Kepler）的一句名言：“数学是这个世界之美的原型。”⑥W·海森堡：《精密科学中美的含义》，曹南燕译，《自然科学哲学问题丛刊》1982年第1期，第40-47页。与此同时，海森堡还赋予了科学美以简单性、和谐性、对称性和完整性等多种美的形式，并将他们作为评判和选择科学理论的标准。这里的“简单性”首先指的是理论体系基础在逻辑上的“简单性”，它与理论体系在结构上的“和谐性”是相一致而互为贯通的。因为在海森堡看来，一个理论前提的简单性越大，它所涉及的事物种类越多，他的应用范围越广。其次指的是数学的简单性，物理定律都是由数学上最简单的概念及其之间的关系组成的。这里的“和谐性”海森堡说的是“部分同部分，部分同整体的固有的协调”。⑦W·海森堡：《精密科学中美的含义》，曹南燕译，《自然科学哲学问题丛刊》1982年第1期，第40-47页。至于数学关系的完整性，海森堡是针对理论形式的完美性而言的。他认为对精密的自然科学来说，数学化是其理论精密性程度的一个主要标志。而数学，从它的学科发展史可以看出，历来是十分讲究和强调形式美的。如方程的对称性、齐次性、内洽性、唯一性；公理化系统必须遵循的相容性、独立性和完备性，等等。对于19与20世纪之交的物理学革命中所脱颖而出的两大理论支柱，海森堡是这样来评判的：“相对论和量子论的出现，……一大堆杂乱无章的细节由于出现了一种联系而几乎马上变得井然有序了，这个联系基本上是非直觉的，但就它的本质来说仍然极其简单，凭借它的完备性和抽象的美，他立即就令人感到信服，——那就是说，使得所有一切能够懂得并说出这样一种抽象语言的人都心悦诚服。”⑧W·海森堡：《精密科学中美的含义》，曹南燕译，《自然科学哲学问题丛刊》1982年第1期，第40-47页。海森堡还认为，如果用“和谐性”这一美学标准来评价牛顿力学，其内在结构所呈现出的“部分与部分彼此之间及部分与整体之间的协调一致”⑨W·海森堡：《精密科学中美的含义》，曹南燕译，《自然科学哲学问题丛刊》1982年第1期，第40-47页。之美，那几乎是不需要加以说明的事。因为在该理论体系之中，部分是个别的力学过程，即我们用仪器小心地加以隔离的那些过程，或者说是那些无法分割的发生在我们眼前的色彩缤纷的现象过程。整体则是所有这些过程都遵守牛顿以简单的公理系统、从数学角度所建立起来的一个统一的形式原则。凡此种种，使得海森堡得出结论说：“数学的秩序，是用来说明现象的多样性的基本原则”，“数学关系也是美的源泉”。⑩W·海森堡：《精密科学中美的含义》，曹南燕译，《自然科学哲学问题丛刊》1982年第1期，第40-47页。

海森堡不仅认为由数学上最简单的概念及其之间的和谐关系所构成的物理定律，赋予了物理学理论大厦以美的特征和美的源泉，而且其简单性与和谐性打着“真”的印记。一则在他看来自然界多样性统一的客观规律，必然能以和谐的数学关系表现出来；二则他强调：“物理学的最重要的真理判据就是一切物理学定律的最终基础的简单性。物理学定律为什么要简单，宽阔的经验领域为什么能有简单表示，答案在于物理学的历史。……非常明显，在公理体系中这些简单而宽阔的公式关系不是人们发明的，而是本来就存在的。这些关系大概是科学的真正内容。”①W.Heisenberg.Physics and Beyond.New York,1971.毋庸置疑，作为著名的物理学家海森堡当然深知，科学的首要目标不是“美”，而是“真”。或者说，在科学中“真”是第一位的，“美”是第二位的。和有些物理学家看问题的角度有所不同的是，海森堡始终是从数学形式的美来论述物理规律的真的。他认为简单而完整的“和谐的数学关系”，虽然渗透着人类主观思维的部分，但却能够充分展示出自然界的本质特征，或者说数学美是自然美的客观反映。否则，如果没有大自然那种内在固有的和谐与秩序美的本质属性，单凭人的主观思维是完全不可能达到如此瑰丽无比的数学形式的。正是立足于这一点，海森堡认定这些数学上最简单的概念及其之间和谐的数学形式应当是物理世界中客观事物规律性的真实反映。借助于意识对物质的反作用——人类独特的创造性，才使完美的数学在表述物理学定律时“具有不可思议的有效性”。②程民治：《从物理学看数学美》，《自然辩证法研究》1995年第12期，第23-27页。这正如海森堡所断言的那样：“在目前情况下，数学体系的这种简单性有了进一步的后果，那就是它应当有可能想出许多实验，而这些实验的结果是能够事先由理论可以预测的。如果事实上有实验证实这些预测，那末，认为这个理论在这一特殊领域内准确地反映了自然界，该是没有什么可怀疑的了。”③许良英等编译：《爱因斯坦文集》（卷1），北京：商务印书馆，1977年，第217页。

海森堡还认为，既然数学美具有客观实在性，那么科学理论不仅可以用最简单的数学形式表示出来，而且还可将科学理论还原为和谐的数学关系。这是为什么呢？海森堡曾反问道：“伟大的联系带着这种美的熠熠光彩进入精密科学，甚至在细节得到了解之前，在能够合理地加以证明之前，就成为可认识的，这是怎么一回事呢？这种启发力量何在？这对于科学进步有何影响？”④W·海森堡：《精密科学中美的含义》，曹南燕译，《自然科学哲学问题丛刊》1982年第1期，第40-47页。针对这种“美”何以认识“真”的问题，海森堡的回答是：“对于现象的丰富多彩的多样性的理解，就出现于在其中认出可以用数学语言来表示的统一的形式原则”。由此，“在可理解的东西和美的东西之间也就建立起一种密切的联系……对美的东西的体验事实上就等同于对联系的体验，不管这些联系是理解到的或者至少是猜测到的。”⑤W·海森堡：《精密科学中美的含义》，曹南燕译，《自然科学哲学问题丛刊》1982年第1期，第40-47页。于是，海森堡进一步深刻地揭示了“美”和“真”之间那种潜在的、必然的有机联系，以及科学美感对于发现科学真理的重要意义。

作为对于那些热切地希望发现新事物的人们的一种告诫和共勉，海森堡指出：“美对于发现真的重要意义在一切时代都得到承认和重视”。⑥W·海森堡：《精密科学中美的含义》，曹南燕译，《自然科学哲学问题丛刊》1982年第1期，第40-47页。并引用了两句拉丁格言：“美是真理的光辉（Pulchritudo splendor veritatis）”，“简单是真的印记（Simplex sigillum veri）”。⑦W·海森堡：《精密科学中美的含义》，曹南燕译，《自然科学哲学问题丛刊》1982年第1期，第40-47页。

海森堡身体力行，正是借助于真理的光辉——美的照耀，来创建他的矩阵力学的。如前文所述，矩阵力学可认为是玻尔理论的一个自然发展。笔者认为，其中对数学美的刻意追求、对玻尔对应原理的普遍意义的深刻认识，以及可观察性（按：观察量的概念实质上取自爱因斯坦的相对论）原则的确立，是海森堡创立量子力学的基本思想。也正因为如此，他毅然决然地抛弃了如上所述的旧量子论中诸如电子轨道和旋转频率之类的不可观测量。

海森堡的矩阵力学理论由三部分组成。第一部分给出了量子论的运动学表述式；第二部分列出了量子论的动力学表述式；第三部分讨论了一个简单非谐振子的应用例子。他的整个论述过程贯穿着对应原理、可观察量思想、克拉默斯（Kramers）的色散理论以及玻恩的经典公式与量子公式的转换规则等的指导，充斥着矩阵这一运算的数学工具所展示出的简单、对称、自洽、和谐之美。在具体推导和运算的过程中，当有关量子力学的规律突然闪现在他的脑海中时，其灵魂深处便迸发出一种强烈的战栗。如海森堡在计算能量矩阵中的各个因子获得成功时，是这样描述他当时的心理感受的：“一天晚上，我就要确定能量表中的各项，也就是我们今天所说的能量矩阵，用的是现在人们可能会认为是很笨拙的计算方法。计算出来的第一项与能量守恒原理相当吻合，我很兴奋，而后我犯了很多的计算错误。终于，当最后一个计算结果出现在我面前时，已经是凌晨3点了。所有各项均能满足能量守恒原理，于是，我不再怀疑我所计算的那种量子力学具有数学上的连贯性与一致性。刚开始，我很惊讶。我感到，透过原子现象的外表，我看到了非同寻常的漂亮的内部结构，并且我必须探求的数学结构特性如此慷慨地展现在我眼前，这一想法几乎使我陶醉。我太兴奋了，以致不能入睡。”①S.Chandrasekhar：《科学的追求及其动机》，周国强译,杨建邺校，《世界科学》1991年第4期，第56-60页。

为了便于说明问题，我们仅以在海森堡工作的基础上，逐步演化而来的一维谐振子的哈密顿量H，在能量表象中的矩阵表示式为例，来说明其间所充斥着的数学美。 即亦对于，我们有：

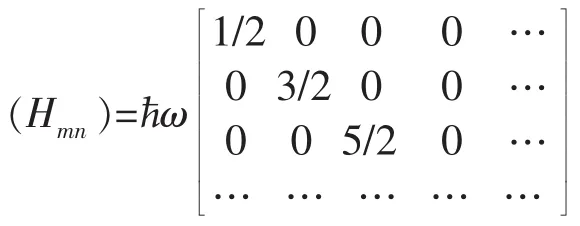
足见，该数学模型构思奇特、新颖、别致。既简单对称（按：从该矩阵的对角线“↘”上看）；又突出了问题的本质。难怪爱因斯坦说：“理论科学家在探索理论时，就不得不愈来愈听从数学的、形式的考虑，因为实验家的物理经验不能把它提高到最抽象的领域中去。”②许良英等编译：《爱因斯坦文集》（卷1），北京：商务印书馆，1977年，第104页。

1926年春天，即在海森堡创建矩阵力学的第二年，他在柏林大学物理系介绍他所创立的量子力学，爱因斯坦（A.Einstein）听了报告后，即邀请他到家中做客，详细讨论了海森堡的新思想，在爱因斯坦连问了许多问题而未获得满意的答复后，爱因斯坦便怀疑地说：“在这么多关键问题还完全没有解决的时候，你怎么能够对你的理论真的有这么大的信心呢？”③许良英等编译：《爱因斯坦文集》（卷1），北京：商务印书馆，1977年，第216页。海森堡迟疑了一会儿说：“我相信自然规律的简单性具有一种客观的特征，它并非只是思维经济的结果。如果自然界把我们引向极其简单而美丽的数学形式——我所说的形式是指假设、公理等等的贯彻一致的体系——引向前人所未见过的形式，我们就不得不认为这些形式是真的，它们是显示出自然界的真正特征。……我们永远不能由我们自己来达到这些形式，它们是自然界显示给我们的。”④S.Chandrasekhar：《科学的追求及其动机》，周国强译,杨建邺校，《世界科学》1991年第4期，第56-60页。

第二次世界大战以后，海森堡在德国科学的重建中起了重要的作用。针对他当时提出并加以阐述的基本粒子理论思想，海森堡曾和他的夫人谈到对称性的奇妙之处在于可以把它看作万物的原型；他还谈到和谐、简朴的美以及它的内在的真实性。⑤S.Chandrasekhar：《科学的追求及其动机》，周国强译,杨建邺校，《世界科学》1991年第4期，第56-60页。海森堡还在当时写给他姐姐的一封信中表述了自己内心的感受：“实际上，过去的几周对我来说是非常激动的时刻。也许通过类比我能将我所经历的事情很好地描述出来。……我费尽心力试图沿一条至今仍不清楚的道路攀登原子理论的顶峰。现在这座顶峰就在我面前，有关原子理论的全部纵横关系，突然地并且清晰地展现在我眼前。这些纵横关系凭借其数学的抽象性以一种简单得不能再简单的方式呈现出来，它是一种我们只能谦恭接受下来的礼物。即使是柏拉图也可能不相信它们是如此之美。因为这些纵横关系不可能被发明，它们从开天辟地以来就一直存在。”⑥S.Chandrasekhar：《科学的追求及其动机》，周国强译,杨建邺校，《世界科学》1991年第4期，第56-60页。

海森堡还将他对对称性的深刻洞察，运用于对统一场论的研究。因为在他看来，对称性应该是某种比粒子本身更基本得多的东西。据此，从1957年开始，海森堡就试图从对称性的数学理论出发，致力于基本粒子统一场论的探索，其目的就在于建立起披露微观粒子体系内禀对称性的漂亮模型。他通过取消狄拉克方程的质量项，添加一个非线性项的方法，把狄拉克方程改造成一个非线性的统一自旋场方程：

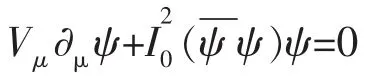
其中ψ是元物质的自旋场。虽然该方程无法把所有的基本粒子与四种相互作用都统一起来。但是求解这个方程，海森堡却获得了一些可喜的成果。其中的一些解可以分别代表质子、π介子和K介子。更为重要的是，该方程为后人提供了大量的、有益的经验与教训。深信各种物理力可以在考虑对称性之美的前提下用一个简单而和谐的理论来作统一的描述，已成了当代理论物理学家孜孜不倦地探求的目标。如今，“小统一”理论已被普遍接受，“大统一”模型层出不穷，创“超弦”也风靡论坛。海森堡所向往的圆满统一，其眉目日趋清晰，真是曲曲凯歌，动人肺腑。

海森堡还认为科学与艺术之间不仅相似相通，而且还能够相互补益、互相促进。当以理性作为认知手段的物理学家站在科学的领地里，用哲学家的头脑去思索人和自然的本质问题时，他的一只脚已经不由自主地踏上了艺术的领地；反过来，艺术家也是如此。所以，在海森堡的科学臻美创造中，能够恰到好处地运用科学思维与艺术思维之间相依相促、兼容互补的关系。在他看来，科学思维决不是那种纯之又纯的抽象的逻辑思维过程，在它当中含有艺术思维的因素。即在科学思维中，抽象与具体、逻辑与非逻辑总是交织在一起的。

海森堡觉得，对于物理世界的认识过程就是一个对新定律、新原理的探求的过程，是一个“猜想-计算结果-与实验比较的过程”。而作为第一步的“猜想”，就是一种审美直觉的过程。没有这种直觉，没有对物理定律所服从的美学观念，诸如对简单性、和谐性、对称性、统一性等的深刻领悟，就无法透过观察和实验事实的表面而直观事物的本质。“然而必须注意把这一直觉的知识转移到意识之中，使它与特殊的、在理性上可以系统表示的理念联系起来”，①W·海森堡：《精密科学中美的含义》，曹南燕译，《自然科学哲学问题丛刊》1982年第1期，第40-47页。才能形成科学理论，发现自然界那种稳而不现的基本结构和普遍性原理。海森堡经常能以直觉体悟的方式对自然的行为得到一种新颖而深刻的理解，并且以令人耳目一新的简洁而完整和谐的数学关系表达出来。他的学生布洛赫曾赞扬海森堡最奇特的品质之一，就是他在处理物理问题时所表现出来的那种几乎万无一失的直觉，以及他的解答似乎自天外飞来的那种非凡方式。显然，作为科学探索过程的第二步“计算结果”和第三步“与实验比较”，无疑是一个抽象的逻辑思维过程。足见，科学思维与艺术思维的交融互补，是海森堡独特的研究风格和科学方法。

概而言之，海森堡作为20世纪国际物理学界顶尖的科学大师，将以他50余年的理论探索，深刻地影响着当代理论物理学的发展。其中特别是他创立矩阵力学的新思路，令人耳目一新。即“从头起就按量子理论的思想对经典力学的运动学加以改造，并立下了运算规则，以后每一步骤都是在量子理论的规则下进行的。可以说，这是对经典力学的彻底革命。”②赵凯华：《创立量子力学的睿智才思（续1）》，《大学物理》2006年第10期，第1-10页。与此同时，海森堡在创立量子力学的过程中，所表现出的一个物理学工作者所必须拥有的哲学家的头脑和气质，也为后继者树立了一个光辉的典范。此外，作为一个科学艺术家，他那种深邃的科学美学思想以及与美偕行的科学方法论，也已成为人类思想宝库中的一份流芳百世的珍品。它必将继续为本世纪物理学的发展开拓着广阔道路，产生着不可估量的深远影响。然而，毕竟人无完人，金无足赤，海森堡也是如此。他的文章虽然包含着很多原创性的闪光的物理学新思想，但绝非完美无缺。对此，杨振宁曾恰到好处地指出：“海森堡的文章，朦胧不清楚，绕着很多的弯，有很多错的地方。所以你看了海森堡的文章，要赶快注意，为什么呢？如果你能够把它的好的地方与坏的地方分清楚，把它坏的地方摒除掉，把它好的地方发展下去，那么你的文章也就变得很重要了。”③杨振宁：《美与物理学》，《浙江大学学报》（社科版）1998年第3期，第1-8页。