谱风险预算投资组合保险模型研究
2013-08-15刘鹏
刘 鹏
(1.中原工学院 经济管理学院,河南 郑州 450007;2.西南交通大学 经济管理学院,四川 成都 610031)
一、引 言
投资组合保险的目的是控制风险,它运用无套利均衡原理,通过基础资产和无风险资产复制出期权进行保险。因而投资组合保险得以实现的重要前提是能够复制出期权。Rubinstein和 Leland (1981)[1]证明当期权是 Black-Scholes(1973)[2]定价形式时,可以通过基础资产与无风险资产的组合复制,从而实现完全的套期保值。但是,Black-Scholes期权定价的一个基本假设是证券市场收益率服从几何布朗运动。事实上,实证研究表明证券市场收益率具有尖峰厚尾的性质,不服从几何布朗运动。研究表明,t分布或布朗运动和双指数跳跃的复合泊松过程能更好地拟合证券市场收益率的尖峰厚尾分布(Kou,2002,2008)[3-4]。由于后者的简单及易处理性[3],本文拟采用双指跳跃扩散过程描述证券价格运动,在此基础上进行风险管理。
套期保值(hedging techniques)和风险预算(risk budgeting)是两种主要的积极风险管理工具(Strassberger,2006)[5]。Kenned,Forsyth和Vetzal(2009)[6]认为在尖峰厚尾的情况下无法实现完全的套期保值,所以本文拟采用风险预算建立投资组合保险模型,实现保值增值。
二、风险预算和谱风险测度
风险预算的首要问题是风险测度,然后是如何控制风险。
风险预算(risk budgeting)至今没有一个统一明确的定义。Chow和Kritzman(2001)[7]认为风险预算是有效的投资组合配置的一个延伸,实际上是将投资组合在不同资产间的配置映射到风险价值VaR的配置过程,而且只有在均值方差最优化的情况下才是有效的,这样投资者才能更好地管理风险。也就是说不应该把风险预算过程看做是有效的资产组合配置的过程,而应该认为风险预算是将有效的资产组合配置转化为VaR配置的一种方法。
Pearson(2002)[8]从狭义和广义的角度论述了风险预算。狭义的风险预算是一个度量和分解风险的过程。用资产配置决策的方法进行测度,根据这些测度安排资产组合经理的风险预算,并且用风险预算来监管资产配置和资产组合经理。风险预算的前提是风险分解,风险分解有助于我们更好地理解所设定的风险以及它们是如何变化的。广义的风险预算是关于投资和资产组合管理的一种观点。由于这个原因,找到一个广泛一致的定义是困难的,甚至是不可能的。但是可以肯定的是风险预算的基础是风险的概率度量或统计度量。
Strassberger(2006)[5]认为风险预算(risk budget)是一定置信区间的下方风险,用VaR或CVaR表示。他给出了当证券市场的收益率服从几何布朗运动时相应的风险预算值并给出了动态的调整方法以实现风险预算。
以上关于风险预算的共同之处是风险预算是一种资产组合管理的方法,管理的重点是风险而不是收益率。风险预算的首要问题是风险度量,然后是如何控制风险。
本文中的风险预算是根据Artzner等人1999年提出的风险概念[9]而建立的。他们认为风险是所需要的一定数量的资产,加入该资产后,初始资产组合头寸在经过一段时间之后是可接受的,即某投资组合的风险是所加入的使该投资组合在未来是可接受的价值的最小资产量。如果风险为正,表示增加到初始投资组合的最小额外资产(现金),如果风险为负,表示可以从资产组合中抽取出来的资产(现金)。
类似于Strassberger(2006)[5]采用VaR或CVaR表示风险预算,本文采用谱风险表示风险预算。
Acerbi(2002)[10]提出的谱风险是一致性风险测度,与投资者的风险厌恶程度相联系,VaR、ES是它的特例。VaR对应于谱风险测度的退化情况,ES反映风险中性,但两者都不能反映投资者的风险厌恶程度。Acerbi(2002)[10]定义的谱风险测度为:

其中,φ∈L1([0,1])称为主观风险厌恶函数。当φ满足非负性、非增性和L1下的模‖‖φ =1时,φ称为可容许谱。Xq为累积分布函数F(x)的q分位数。
由(1)式知,谱风险测度是对分位数Xq赋予权重φ(q)的积分。φ(q)是一个非负非增函数,也就是说随着风险的减小,权重并没有增加,即投资者对较大的风险赋予较大的权重,而对较小的风险赋予较小或相当的权重,这与人们的风险态度相吻合。
三、基于谱风险测度的风险预算投资组合保险模型
股价时有跳跃,市场收益率分布具有尖峰厚尾的特征。因此,Merton(1976)[11]提出用跳跃扩散模型来描述证券市场收益率分布,他假设跳跃的大小服从正态分布;Kou(2002)[3]认为跳跃的大小服从双指数分布并假定资产价格服从随机微分方程:

(2) 式中, μd t是漂移项; σd W 是扩散过程;表示跳跃过程;μ为漂移参数;σ为扩散参数;Wt是一个维纳过程;Nt为跳跃强度为κ的泊松过程;是独立同分布的非负随机变量序列,记Y=ln(J),Y服从双指数分布,概率密度函数为:

p为向上跳跃的概率。可以得到:
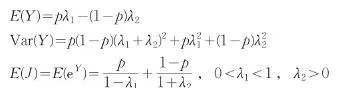
随机微分方程(2)式的解为:
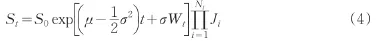
本文中的盈利或损失是指全部资产投资到无风险资产上的期末价值与全部资产投资到风险资产上的期末价值的差,即

显见,Lt>0表示损失,Lt<0表示盈利。由于ST为一随机变量,Lt也是一随机变量,相应的分位数函数记为:

假设φ为指数形式的风险厌恶函数,即

该函数具有常绝对风险厌恶系数k(k>0)。则相应的风险预算为:

为了避免损失,又不失去从市场上升中获利的机会,将资产在无风险资产与风险资产之间分配。假设t时刻资产总值为At,投资在无风险资产上的比例为wt,期末价值为wtAter(T-t),则投资在风险资产上的比例为1-wt,投资组合的风险预算等于风险资产的风险预算,即,根据邹晓芃等(2006)[12]提出的用无风险资产的收益套补投资组合的风险预算,则有:

即

由(8)式可知,投资在无风险资产的比重与风险预算有关,风险预算越大,投资在无风险资产的比重越大,反之依然。而且投资在无风险资产的比重与人们的风险厌恶程度相关,风险厌恶程度越大,投资在无风险资产上的比例越大,见(10)式。


故(9)式变为:

本文建立的模型用谱风险表示风险预算,不断调整总资产在无风险资产与风险资产间的分配,达到规避风险并获取市场上升收益的目的,因此称该模型为谱风险预算投资组合保险模型(Spectral Risk Budget Portfolio Insurance Model)。
四、案例模拟分析
以“上证综指”作为风险资产,对上文建立的谱风险投资组合保险模型进行案例模拟分析。首先计算谱风险预算,其次是根据(10)式将总资产在无风险资产与风险资产之间分配,期限为一年。
谱风险预算是根据上证综指的历史数据模拟得到。根据(8)式,计算谱风险预算需要知道分位数及风险厌恶函数,分位数的取得是根据(5)式的跳跃扩散过程取得。利用跳跃扩散描述的是市场的尖峰厚尾性质,因此,这里采用指数而不是单一股票作为风险资产,由(5)式描述其运动状态,预测价格,得到相应的分位数。案例模拟中首先根据胡素华 (2006)等[13]及任枫 (2009)[14]等对上证综指有关参数的估计,取收益率的年均值μ=-0.064,年标准差σ=0.4,假定每年跳跃3次,即 κ=3, p=0.54,λ1=1/15,λ2=1/17,无风险利率r=0.03,每年的交易日为250天,对(5)式进行模拟,模拟路径为10000条,然后得到分位数,根据(8)式计算出绝对风险厌恶系数分别取k=1,2,3,4,5,6,15,20,25的谱风险预算。得到谱风险预算后,根据(11)式将总资产在无风险资产与风险资产之间配置。(11)式中的St通过Block Bootstrap抽样得到,为保持模拟的可靠性,数据区间与胡素华等(2006)[13]、任枫等(2009)[14]的相同,为上证综指1992年5月1日至2004年4月30日12年的数据。
投资组合保险绩效的评价准则本文中采用了期末资产、超额收益率、SHARPE比率及VaR和ES(刘鹏、史本山,2010)[15]。由于VaR、ES评价准则需要大量的样本,因此本文重复模拟过程10000次,得到在一般情况下谱风险预算投资组合保险的绩效。结果见表1。本文模拟采用MATLAB编程实现。

表1 不同风险厌恶程度的谱风险预算投资组合保险绩效
表1表明,随着风险厌恶程度的增加,投资组合的收益率及最终资产价值是递减的,甚至低于无风险收益率,但是都能达到对初始资产的保险作用。究其原因,当风险厌恶程度小的时候,较多的资产投资在风险资产上,能够获得市场上涨的收益,而当市场下跌时则能及时将资产投资到无风险资产上,锁定已获得的收益。但是随着风险厌恶程度的增加,投资到风险资产上的份额较少,因此市场上升时获得的收益也较少,甚至会出现达不到无风险资产收益率的情况。另外,随着投资者绝对风险厌恶系数的增加,超额收益率、SHARPE比率下降较快,而VaR和ES递减,说明该模型更好地规避下方风险。
表2对比了本文建立的谱风险预算投资组合保险模型与CPPI、OBPI策略的绩效。后两者的绩效模拟同样是采用Block Bootstrap抽样方法进行。结果表明在绝对风险厌恶系数k=4时,谱风险预算投资组合保险模型的绩效与CPPI、OBPI策略较为接近。Cotter和 Dowd (2006)[16]认为一般人的绝对风险厌恶系数为4,证明该模型具有合理性。同时,当风险厌恶程度较低(k<4),以期末资产、超额收益率及SHARPE比率作为评价标准,谱风险预算投资组合保险模型的绩效优于CPPI、OBPI策略,因此,该模型丰富了投资组合保险模型,为不同的风险厌恶者提供了选择的机会。

表2 谱风险预算投资组合保险绩效与CPPI、OBPI的绩效比较
五、结束语
由于几何布朗运动描述证券市场收益率存在的缺陷,所以本文采用双指数跳跃扩散过程来克服这一问题。但跳跃的存在导致不能实现完全的套期保值,因而本文采用风险预算建立投资组合保险模型。风险预算一般由VaR表示,但VaR不是一致性风险度量,所以本文引入谱风险来表示风险预算。模拟结果表明本文建立的谱风险预算投资组合保险模型能有效规避下方风险,并随着投资者风险厌恶程度的增加,投资组合的绩效下降;对于一般风险厌恶的投资者,该模型绩效与CPPI、OBPI策略的绩效接近,当投资者的风险厌恶程度较低时,以期末资产、超额收益率、SHARPE比率衡量的绩效优于CPPI、OBPI策略。
[1]Rubinstein M,Leland H.Replicating Options with Positions in Stock and Cash[J].Financial Analysis Journal,1981,37(4):63-72.
[2]Black F,Scholes M.The Pricing of Options and Corporate Liabilities[J].Journal of Political Economy,1973,81(3):637-659.
[3]Kou S C.A Jump-Diffusion Model for Option Pricing[J].Management Science,2002,48(8):1086-1101.
[4]Kou SG.Jump Diffusion Models for Asset Pricing in Financial Engineering[C]//Birnge J R,Linetsky V.Handbooks in OR and MS.Amsterdam:Elsevier BV,2008:73-116.
[5]Strassberger M.Capital Requirement,Portfolio Risk Insurance,and Dynamic Risk Budgeting[J].Investment Management and Financial Innovations,2006,3(1):78-88.
[6]Kennedy JS,Forsyth PA,Vetzal K R.Dynamic Hedging under Jump Diffusion with Transaction Costs[J].Operations Research,2009,57(3):541-559.
[7]Chow G,Kritzman M.Risk Budgets[J].The Journal of Portfolio Management,2001(winter):56-61.
[8]Pearson N D.Risk Budgeting:Portfolio Problem Solving with Value-at-Risk[M].New YorK:John Wiley&Sons,Inc.,2002:1-33.
[9]Artzner P,Delbaen F,Eber JM,et al.Coherent measures of risk[J].Mathematical Finance 1999,9(3):203-228.
[10]Acerbi C.Spectral Measures of Risk:a Coherent Representation of Subjective Risk Aversion[J].Journal of Banking&Finance,2002,26(7):1505-1518.
[11]Merton C.Options Pricing When Underlying Stock Returns Are Discontinuous[J].Journal of Financial Economics,1976,3(1/2):125-144.
[12]邹晓芃,钱英,俞君.基于VaR的权变投资组合保险策略及实证分析[J].数理统计与管理,2006,25(2):195-204.
[13]胡素华,张世英,张彤.双指数跳跃扩散模型MCMC的估计[J].系统工程学报,2006,21(2):113-118.
[14]任枫,汪波,段晶晶.非对称双指数跳跃扩散模型的MCMC估计[J].系统工程,2009,27(7):39-42.
[15]刘鹏,史本山.投资组合保险绩效评价——基于VaR和ES的实证研究[J].西南交通大学学报(社会科学版),2010,11(4):61-64.
[16]Cotter J,Dowd K.Extreme Spectral Risk Measures:an Application to Futures Clearinghouse Margin Requirements[J].Journal of Bank Finance,2006,30(12):3469-3485.
