延迟积分微分方程二步Runge-Kutta法渐近稳定性分析
2013-08-13袁海燕曲绍平
袁海燕,曲绍平,贺 丹
(黑龙江工程学院 数学系,黑龙江 哈尔滨150050)
近年来,有关延迟微分方程(DDEs)数值方法稳定性的研究越来越多[1-3],这些方程广泛出现于科学工程领域,如电路分析、计算机辅助设计、光学控制等。同期出现了有关模糊延迟微分方程组的结论,例如,多芯片的互连问题[4]。Zhu和Petzold用θ方法、Runge-Kutta方法、BDF方法和线性多步法[5]验证过模糊延迟微分方程的渐近稳定性,Yu用多步法研究了一般中立型延迟微分代数方程(GNDDAEs)[6]。 最 近,人 们 对 延 迟 积 分 微 分 方 程(DIDEs)的研究越来越多。
本文主要探讨延迟积分微分方程(DIDEs)的二步Runge-Kutta方法和它的稳定区域,给出并证明DIDEs的二步Runge-Kutta方法的渐近稳定性结果。
1 二步龙格-库塔方法和它的稳定域
考虑二步龙格-库塔方法(TSRK)具有如下形式:

其中:tj=tn+cjh,~tj=tn-1+cjh,0≤θ≤1;ui是u(ti)的一个近似;h是固定步长;θ,^bj,~bj和~ai,j,cj是系数。这些方法形成了一类一般线性方法[7],也可以看作二步分裂方法。这里,将式(1)~(3)表示为

将式(1)~(3)应用到实验方程
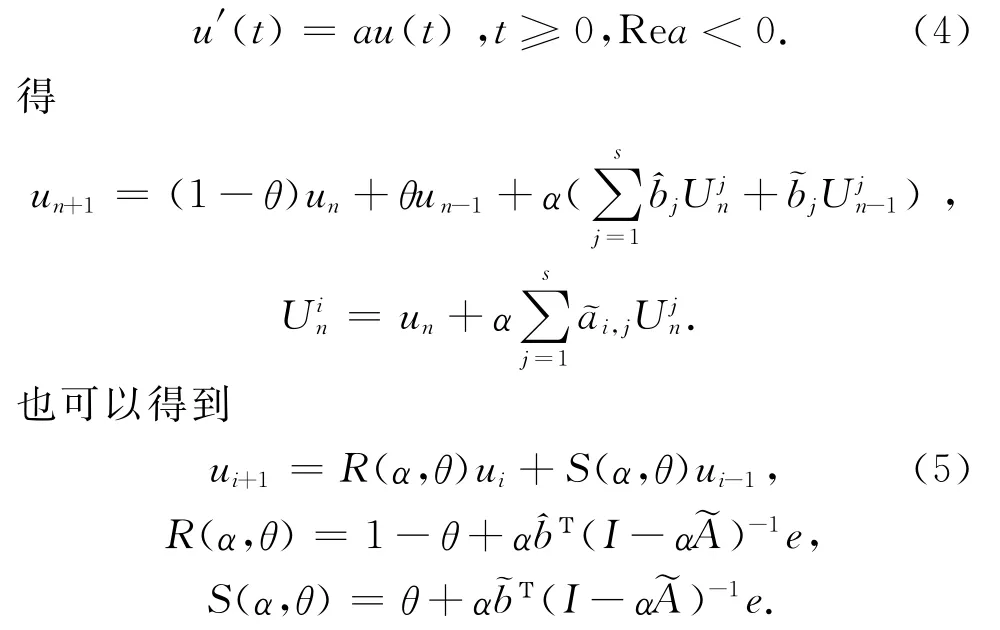
为了研究式(1)~(3)的稳定性,必须分析式(5)解的渐近性,由下面的特征多项式的根决定
φ(z)=z2-R(a,θ)z-S(a,θ).
二步龙格-库塔方法的稳定区域是所有使得φ(z)的根在单位圆内或圆上的α的集合,其中φ(z)在单位圆上的根是单根。如果对于任意的α,Reα<0,φ(z)是一个schur多项式,二步龙格-库塔方法的稳定区域包含负半平面,则称此方法是A-稳定的。
2 NMDIDAEs的TSRK 方法的渐近稳定性
这里考虑方程

假定τq=qτ,τ=Mh,M 是一个正整数,q=1,2,…,m。
定义[8]如果一个数值方法用到渐近稳定系统(6)上的数值解满足=0,则该方法就是渐近稳定的。
将式(1)~(3)代入到式(6)中,得

其中 Kn,i=,i=1,2,…,s是乘h 的级导数。记^bT=[^b1,^b2,…,^bs],~bT=,…,~bs],~A=(~aij)。
假定~A的特征值都有正实部,上述的龙格-库塔方法一定存在。一个简单的例子就是具有正对角系数半显式的龙格-库塔方法[9],重排级导数得到

引理1[10]如果式(10)的所有零点都满足<1,则数值方法式(7)~(8)满足=0。

矩阵Is-λl(r(z))的可逆性意味着对于所有的l,j,λl(r(z))λj()≠1,因 此,有≥1时,det [T1(z)]≠0。
定理 如果系统式(7)~(8)满足引理2的条件且满足下列条件:

则式(7)~(8)的TSRK法的解是渐近稳定的。

结合式(13)和式(14)得

3 结束语
本文主要探讨了延迟积分微分方程(DIDEs)的二步Runge-Kutta方法和它的稳定区域,给出并证明A-稳定的二步Runge-Kutta方法求解DIDEs的渐近稳定性。
[1]Brenan K E,Campbell S L,Petzold L R.Numerical Solution of Initial-Value Problem in Differential-Algebraic Equations[M].2nd ed.Philadephia:SIAM,1995.
[2]Hairer E,Norsett S P,Wanner G.Solving Ordinary Differential-Algebraic Equations and Differential-Algebraic Problems[M].NewYork:Springer,1992.
[3]Petzold L R.Numerical Solutions of Differential-Algebraic Equations[M].Oxford:Clarendon Press,1995.
[4]Brayton R K,Willoughby R A.On the numerical integration of a symmetric system of difference-differential equations of neutral type[J].J.Math.Anal.Appl.1967,18:182-189.
[5]Zhu W J,Petzold L R.Asymptotic stability of linear delay differential-algebraic equations and numerical methods[C].Appl.Numer.Math.1997,24:247-264.
[6]Cong Y H,Sun L P,Li Y.Asymptotic Stability of linear multistep methods for generalized neutral delay differential-algebraic equations[J].Journal of System Simulation,2009,21(20):6432-6435.
[7]Butcher J C.The Numerical Analysis of Ordinary Differential Equations[M].New York:John Wiley & Sons.Chichester,1987.
[8]Wang Q,Cong Y H,Li J J.Stability of two-step Runge-Kutta methods for neutral delay-integro-differential-algebraic equations[J].Journal of Shanghai Normal University(Natural Sciences).2010;39(6):551-557.
[9]Ascher U M,Petzold L R.The numerical solution of delay-differential-algebraic equations of retarded and neutral type[J].SIAM J.Numer.Anal.1995,32:1635-1657.
[10]Lancaster,P,Tismenetsky M.The Theory of Matrices[M].Orlando:Academic,1985.
[11]Campbell S L.Singular linear systems of differential equations with delays[J].Appl.Anal.1980,2:129-136.
